Образцы решения заданий.
1.
Бинарное соответствие
из множества
в множество
состоит из пар: (1;b),(1;d),(2;а),(2;b),(4;с).
1) Указать область определения , т. е. pr А ,
2) Указать область определения , т. е. pr B ,
3) Построить график ,
4) Построить граф .
Решение.
1)
,
2)
.
3
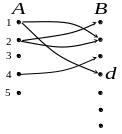) 4)
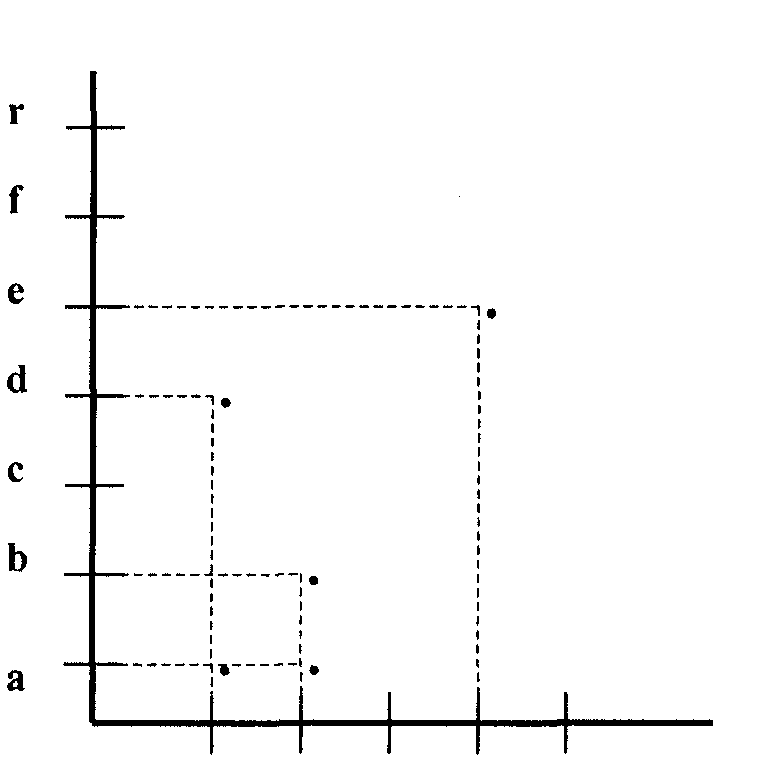
2.
Составить отношения
и
для отношения
на множестве
.
Решение.
1)
.
2)
.
3. Даны подмножества
и
– множества натуральных чисел.
Соответствие
из
в
таково:
число
больше числа
(
,
).
1) Записать с помощью пар.
2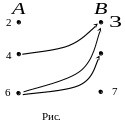
)
Записать
в виде
.
3) Построить граф .
Решение.
1)
.
2)
4
3,
6
3,
6
5,
если 4 больше 3, 6 больше 3, 6 больше 5, или
,
,
.
3)
Упражнения
1.
Даны да множества слов:
{“желтый”,
“белое”, “черная”}, В = {“лист”, “ночь”,
“платье”, “шаль”, “безмолвие”}.
1) Составить бинарное соответствие из и , которое состоит из пар, в которых первая компонента – слово из , а вторая компонента – согласованное с ним слово из .
2)Построить график этого соответствия.
3)Построить граф этого соответствия.
2. Пусть X = { «река», «возвышенность», «океан», «пустыня» }, а У = { а,е,н,я }.
1) Составить декартовое произведение Х У этих множеств.
2) Отметьте в нем пары, связанные соответствием р:
хру <=> « в слово х входит буква у».
3) Задайте это же соответствие при помощи графа.
4) Найдите полный образ слова «океан».
5) Найдите полный прообраз буквы «а».
6) Есть ли в множестве У буква, полный прообраз которой состоит из всего множества X?
7) Есть ли в множестве У буква с пустым полным прообразом?
3.
Для множеств
и
заданы следующие
соответствия:
а)
;
б)
;
в)
;
г)
,
(
,
).
Для каждого из них:
1) найти область определения,
2) множество значений,
3) построить граф,
4) построить график.
Индивидуальное задание.
1.
Даны два множества:
,
.
Поставим в соответствие каждому числу
его квадрат в
.
Выпишите все пары, входящие в указанное
соответствие. Постройте его граф.
2. Соответствие из в задано при помощи графа:
в
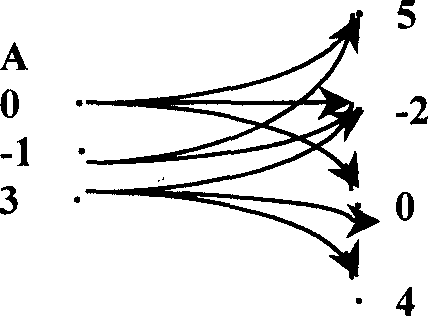
Изобразите график этого соответствия. Постройте график противоположного соответствия.
3. Даны множества: Х={х|х Z,-3≤х<0}, У= Z,. Каждому значению х Х поставим в соответствие такое значение у У, которое на 3 больше этого х. Перечислите элементы, принадлежащие этому соответствию. Постройте граф этого соответствия.
4.
Соответствие р из множества
= { х | х
Z,0≤х≤4}в
множество У= {у|у
Z,
0 ≤ у ≤ 5 } состоит из пар (х;у) таких, что
х < у. Построить граф этого соответствия.
5.
На рис. 1 изображен график соответствия
из А
R
в В
R.
а)
Верно ли ,что 2
А,
2
А,-З
А?
б)Верно ли, что 0 В, -1 В, 0,7 В?
в)Какие значения у В соответствуют -1? О? 7?
г)Каковы область определения и множество значений данного соответствия?
6.
Соответствие р: «хру
число х кратно числу у» задано из
множества Х={135,0,264,122 } в множество У = {
3,4,5,9 }. Построить граф соответствия р .
Найти р (135). Проверить, верно ли р (264) =
3. Найти полный прообраз числа 0.
7. Даны множества А={1;3},В={ 2;5 }. Перечислить все подмножества множества АхВ. Какое из полученных подмножеств задает соответствие:
а) «меньше»,
б) «больше»,
в) «больше или равно»,
г) «быть делителем»?
Построить граф каждого из этих соответствий.
8. На рис. 2 изображен график соответствия р из множества Х в множество У.
а) 3апишите область определения и множество значений этого соответствия.
б) Перечислите все элементы этого соответствия.
в) Постройте граф этого соответствия.
9. Найдите область определения и множество. значений для соответствия а ≤ в, если а и в – натуральные числа и 2 ≤ а < 10, 4≤ в < 12. Постройте граф и график этого соответствия.
10.
Каждой точке М диаметра АВ окружности
на рис. 3 поставим в соответствие те
точки окружности, которые лежат на
перпендикуляре, восстановленном в этой
точке( например, М
К1,М
К2).
а) Отметьте точки окружности, соответствующие точке Д.
б) Отметьте точки диаметра, которым соответствует точка Р, точка С.
в) Какова область исхода и область прибытия данного соответствия?
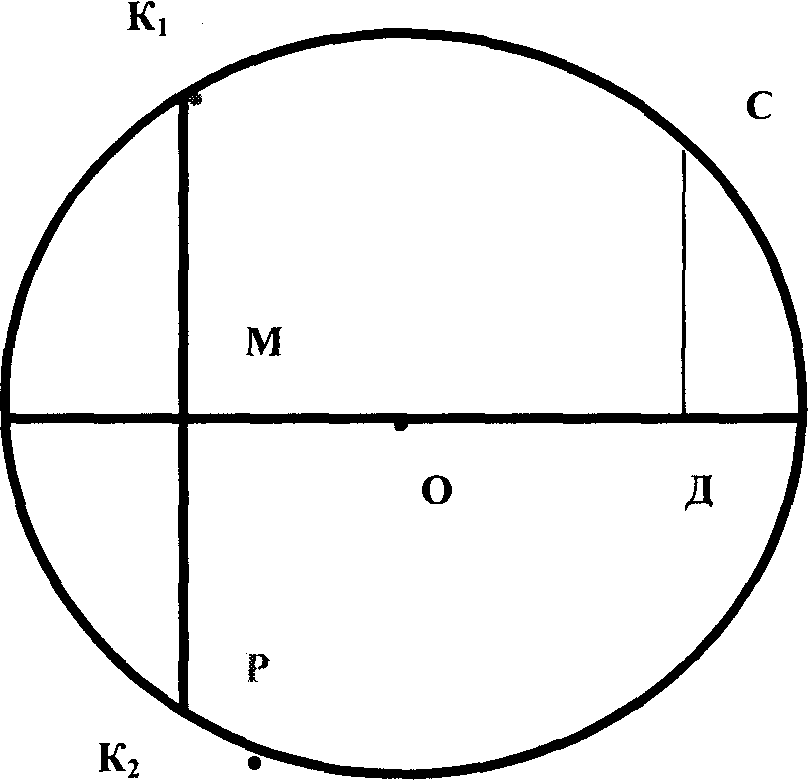
рис. 3