9. Рациональные корни многочлена с рациональными коэффициентами

Многочлен с рациональными коэффициентами имеет те же корни, что и многочлен с целыми коэффициентами, полученного умножением на наименьшее общее кратное всех знаменателей коэффициентов многочлена .

Рациональные корни многочлена , , , находятся в множестве рациональных дробей вида , где – делители числа , – делители числа . Если , то все рациональные корни многочлена будут целыми и находится среди делителей .

Задача 30. Найти все рациональные корни многочлена

.

Решение.

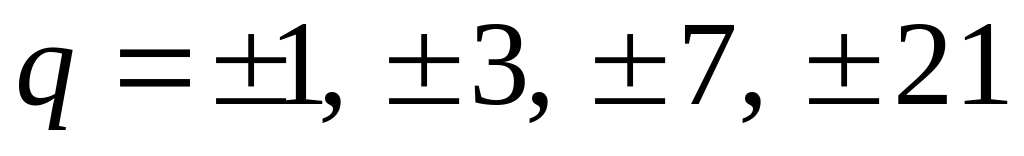1. Найдем все делители числа 21: .

2. Найдем все делители числа 2: .

3. Составим дроби вида : . (Значения берем только положительные, т. к. если – отрицательное, то будет повторение значений ).

4. Применяя схему Горнера, проверим, какие из дробей являются корнями многочлена . Ими будут числа 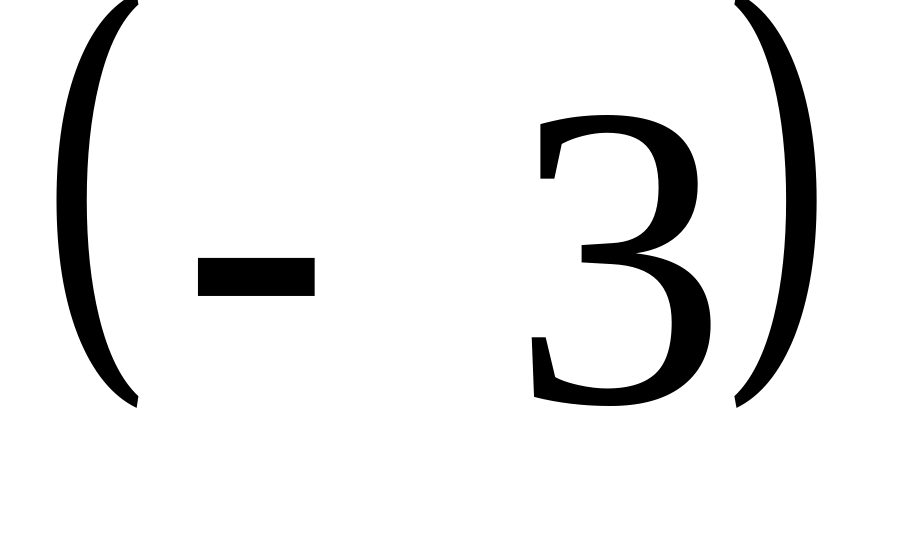и .

25