1.5. Усиление электромагнитных к0лебаний в активной среде

Пусть имеется активный элемент как угодно большой длины, ориентированный вдоль оси z. Активный элемент - это элемент, содержащий рабочее вещество, в котором в процессе накачки создается активная среда.

Активный элемент характеризуется коэффициентом нерезонансных потерь , численно равным обратной величине расстояния, на котором мощность распространяющихся электромагнитных колебаний уменьшается в е раз (размерность: см ).

В активном элементе создана активная среда с инверсной населенностью уровней рабочего перехода . Здесь N₀ – начальное значение инверсной населенности, т.е. в отсутствии поля. Инверсная населенность обеспечивает начальное значение относительного показателя (коэффициента) усиления.

(1.21)

где - эффективное сечение перехода, зависящее от характеристик квантового перехода и имеющее размерность площади. В этом случае (т.е. в отсутствие поля) показатель усиления называется ненасыщенным.

В общем случае значение относительного коэффициента усиления

(1.22)

где - спектральная мощность излучения, распространяющегося в активном элементе вдоль оси z. Размерность

В соответствии со сказанным в пункте 1.4

; (1.23)

В зависимости от вида уширения спектральной линии эффективное сечение перехода может быть найдено из следующих соотношений:

- при однородном уширении

(1.24)

- при неоднородном уширении

(1.25)

Предположим, что на вход активного элемента поступает плоская монохроматическая волна мощностью . Определим, как будет изменяться мощность волны по мере ее распространения в активном элементе вдоль оси z.

Выделим бесконечно тонкий слой активного элемента dz и найдем изменение мощности излучения в этом слое:

-приращение мощности за счет усиления

(1.26)

- уменьшение мощности за счет потерь

(1.27)

-полное изменение мощности

(1.28)

Если в процессе распространения электромагнитной волны инверсная населенность сохраняется неизменной ( ), то и показатель усиления остается постоянным, т.е. . В этом случае дифференциальное уравнение (1.28), есть уравнение с разделяющимися переменными и оно имеет следующее решение:

(1.29)

Соотношение (1.29) носит название интегрального закона Бугера.

Этот закон был экспериментально открыт французским ученым П. Бугером еще в 1729 году для поглощения в веществе слабых световых потоков. До появления квантовых усилителей и генераторов под понимался только коэффициент поглощения.

Полный (интегральный) коэффициент усиления, реализуемый на активном элементе определенной длины

(1.30)

В случае, когда усиление значительно, коэффициент усиления указывают в децибелах:

(1.31)

На практике могут иметь три случая.

В первом случае, при , полный коэффициент усиления К < 1 - происходит ослабление излучения.

Во втором случае, при коэффициент К = 1 - излучение проходит через активный элемент не изменяясь (мощности вынужденного излучения достаточно только для компенсации потерь).

В третьем случае, наиболее интересном для практики, при наблюдается экспоненциальный рост мощности по мере распространения электромагнитной волны вдоль активного элемента. Однако, экспоненциальный рост мощности будет иметь место только при малых мощностях усиливаемых колебаний. Критерием малости служит ситуация, когда за счет вынужденных переходов инверсная населенность практически не изменяется ( , соответственно примерно постоянным остается и показатель усиления .

Но по мере увеличения мощности возрастает и вероятности вынужденных переходов p_ВН и p_НВ пропорциональные этой мощности, соответственно, возрастает и скорость переходов υ_i k  = N_i p_i k (i, k – уровни перехода). Поскольку в активной среде всегда , а p_ВН = p_НВ (для невырожденных уровней), то и инверсная населенность N уменьшается. Уменьшение инверсной населенности по пути распространения в активном элементе электромагнитной волны вызывает соответствующее уменьшение показателя усиления . Рост мощности замедляется (уменьшается производная ). Закон Бугера нарушается. А при падении показателя усиления до уровня коэффициента потерь γ рост мощности прекращается ( ).

Таким образом, при распространении электромагнитной волны в реальном активном элементе показатель усиления вдоль оси z будет, уменьшаясь, стремиться к коэффициенту потерь γ. При этом мощность, возрастая, будет стремиться к некоторому предельному значению , не зависящему от величины и соответствующему компенсации усиления и потерь, т.е. .

Рис.1.6

На рис.1.6 изображены зависимости , , от длины пути z при различных величинах мощности излучения на входе активного элемента.

Кривая 1 соответствует экспоненциальному закону возрастания мощности волны , что имеет место при << , Кривые 2 и 3 показывают ход изменения и при < , а кривые 4 - при  > .

Величина предельной мощности может быть найдена из соотношения:

(1.32)

где S - площадь поперечного активного элемента; - время жизни верхнего уровня рабочего перехода.

Предельная мощность существенно зависит от коэффициента потерь γ. Чем меньше γ, тем выше . Если бы удалось создать среду без потерь ( ), то значение стремилась бы к бесконечности.

В связи с насыщением усиления на частоте ν происходит деформация спектральной линии усиления. При этом характер деформации определяется видом уширения (см. п.1.3).

На рис. 1.7 представлены спектральные линии усиления, соответствующие кривым 1, 2, 3 для z = z΄: а - для однородного уширения, б - для неоднородного.

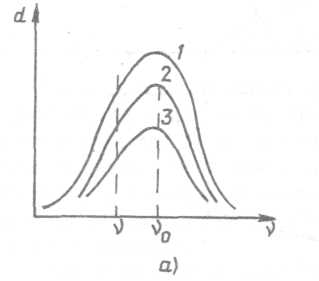
Рис. 1.7

На практике для выбора режима работы усилителя с активным элементом длиной используют амплитудную характеристику, представляющую собой зависимость выходной мощности от мощности на входе при фиксированной мощности накачки.

Такая характеристика показана на рис.1.8 а). Здесь же показана зависимость от . Из рисунка видно, что амплитудная характеристика имеет две характерные области:

I - область линейного усиления, где коэффициент усиления неизменен и велик, здесь соблюдается закон Бугера;

П - область насыщения, где разность между показателями усиления и потерь стремится к нулю, а стремится к .

На рис.1.8 6) показана зависимость коэффициента полезного действия: от .

Видно, что при входной мощности  = 0 и = КПД равен нулю. В области линейного усиления КПД низкий, так как здесь мало приращение мощности из-за малой вероятности вынужденных переходов. Область насыщения энергетически более выгодна.

Максимум КПД соответствует входным мощностям, близким к .

На практике область I может быть использована при усилении слабых сигналов, где требуются большие коэффициенты усиления (приращение мощности при этом невелико). Оконечные же каскады, например, усилительного тракта лазерного передатчика, где требуются значительные приращения мощности (энергии), должны работать в режиме насыщения при сравнительно небольших коэффициентах усиления К.