Формула Байеса
Пусть H1,H2,...,Hn - полная группа событий и А - некоторое событие. Тогда по формуле для условной вероятности
Здесь P(Hk /A) - условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло.
По теореме умножения вероятностей числитель формулы можно представить в виде
P(Hk∩A) = P(A∩Hk) = P(A /Hk) P(Hk)
Для представления знаменателя формулы можно использовать формулу полной вероятности
P(A)
Теперь можно получить формулу, называемую формулой Байеса:
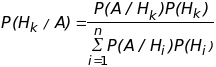
Замечание. По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез.
Замечание. Вероятности P(Hk ) (k=I,2, ... , n) событий H1,H2,...,Hn
до опыта называются априорными вероятностями (от латинского a priori, что означает "сперва", Т.е. в данном случае до того, как был произведен опыт). ' Вероятности P(Hk ) (k = 1,2, ... , n) тех же событий называются апостериорными (от латинского слова а posteriori, что означает "после", Т.е. в данном случае после опыта).
Пример 1.Рассмотрим приведенную выше задачу об учебниках, только изменим вопрос задачи. Пусть библиотекарь получил на складе учебник, и он оказался бракованным. Найти вероятность того, что этот учебник был напечатан во второй типографии.
Выпишем формулу Байеса для этого случая
Из этой формулы получаем: P(H2 / A) = 15/34
.
Приложение. Парадокс независимости
Гл.1 § 4 книги Г.Секей «Парадоксы теории вероятностей и математической статистики»
Дополнение. Из книги Г.Секей «Парадоксы теории вероятностей и математической статистики», глава I «Парадоксы теории вероятностей», §13.Еще несколько парадоксов
