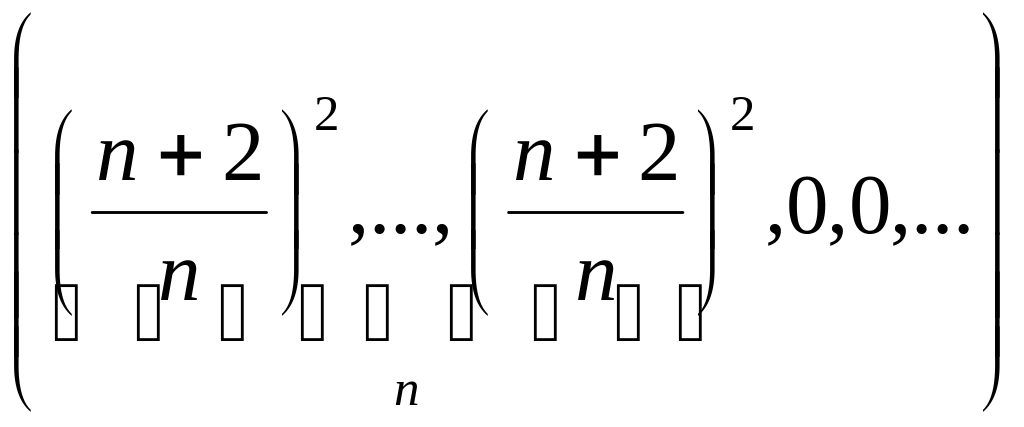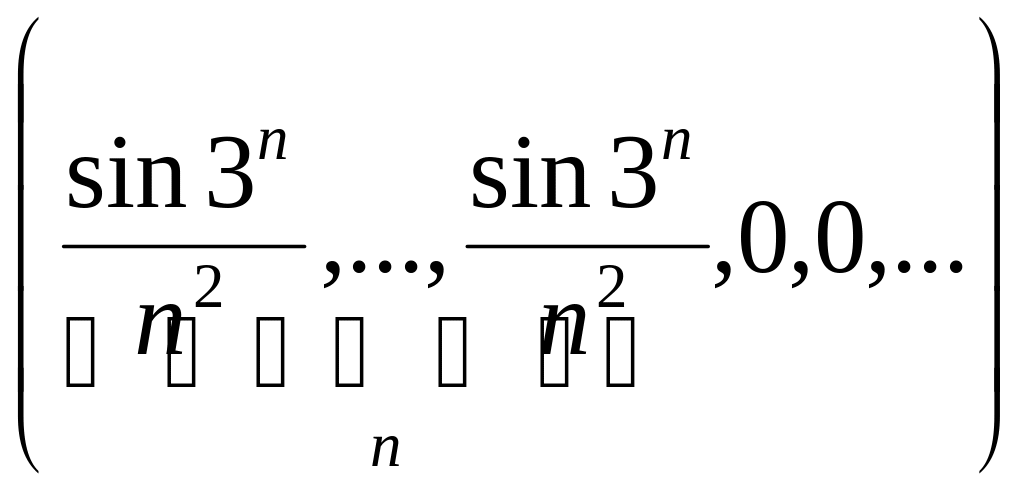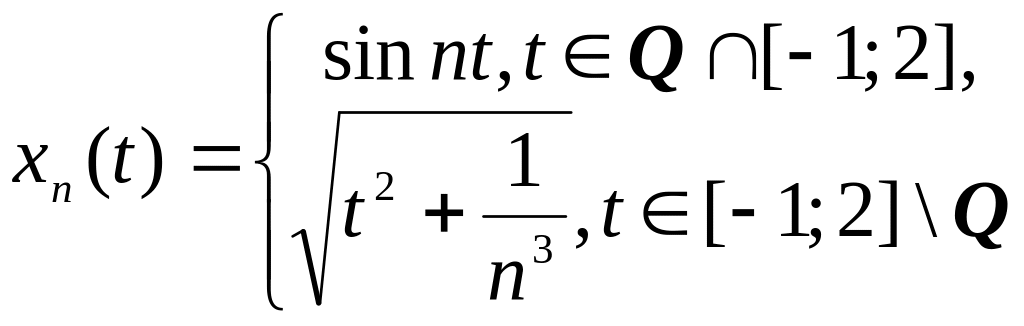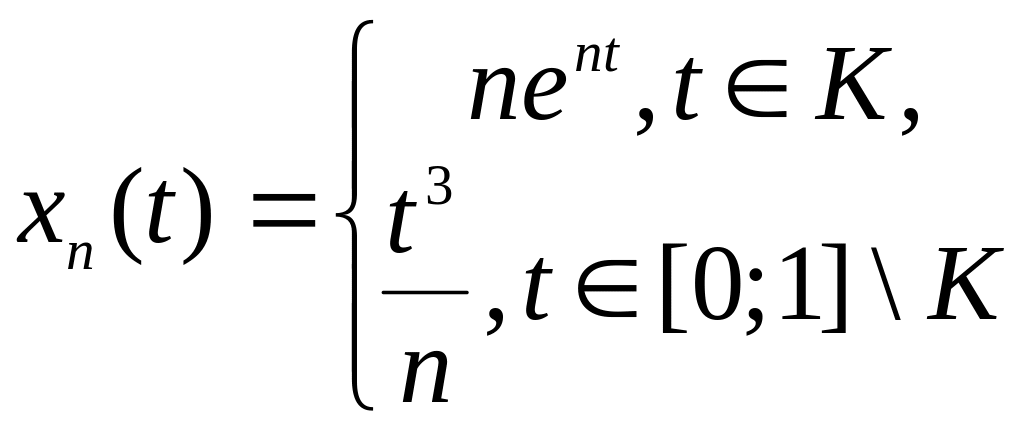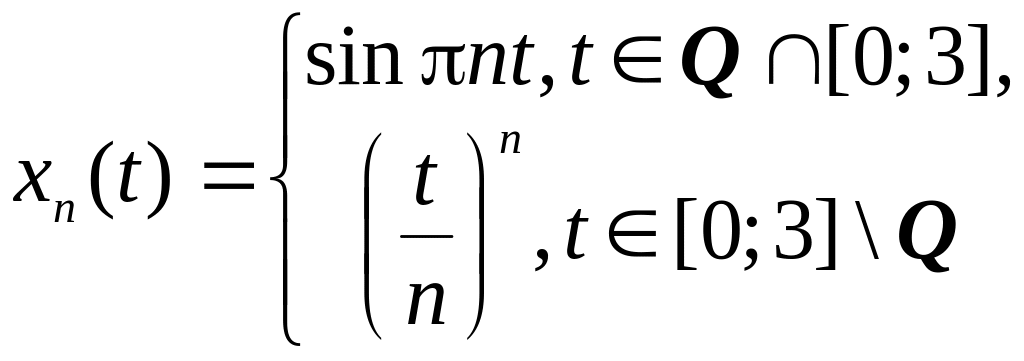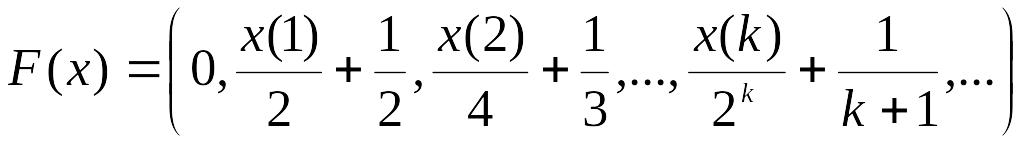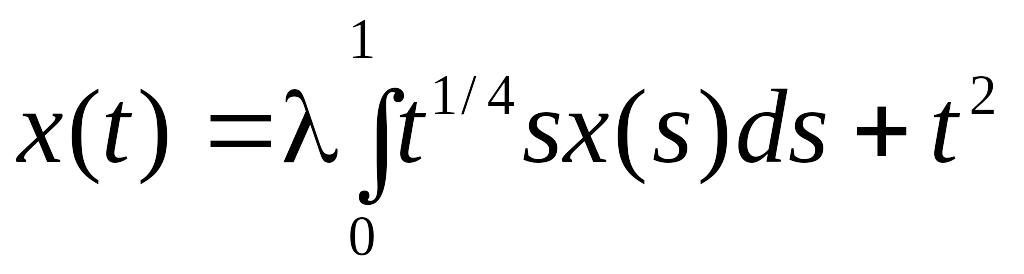- •2 Метрические пространства
- •2.1.2 Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.2).
- •2.1.3 Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.3).
- •3 Линейные нормированные пространства и операторы в них
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
А. Р. МИРОТИН, Ж. Н. КУЛЬБАКОВА,
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
СБОРНИК ЗАДАЧ
для студентов специальности 1-31 03 01 02 –
«Математика (научно-педагогическая деятельность)»
Гомель
ГГУ им. Ф. Скорины
2010
2 Метрические пространства
Тема 1
Сходящиеся последовательности в метрических
пространствах
2.1.1 Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.1).
Таблица 2.1.1
Вариант |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
2.1.2 Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.2).
Таблица 2.1.2
Вариант |
X |
|
|
1 |
2 |
3 |
4 |
1 |
|
|
|
2 |
|
|
|
Окончание таблицы 2.1.2
1 |
2 |
3 |
4 |
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
2.1.3 Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.3).
Таблица 2.1.3
Вариант |
X |
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
2.1.4 Определить, является ли данное условие: а) необходимым, б) достаточным, в) необходимым и достаточным для сходимости последовательности xn в метрическом пространстве X (таблица 2.1.4)?
Таблица 2.1.4
Вариант |
X |
Условие |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
существует предел числовой последовательности |
5 |
|
|
6 |
|
|
2.1.5 Найти предел последовательности xn в метрическом простран-стве X, если он существует (таблица 2.1.5).
Таблица 2.1.5
Вариант |
X |
|
1 |
2 |
3 |
1 |
|
|
2 |
|
|
3 |
|
|
Окончание таблицы 2.1.5
1 |
2 |
3 |
4 |
|
|
5 |
|
|
6 |
|
|
Тема 2
Топология метрических пространств
2.2.1
Является ли данное множество М
открытым, замкнутым, ограниченным в
пространстве
![]() ?
Найти его замыкание, внутренние и
граничные точки (таблица 2.2.1).
?
Найти его замыкание, внутренние и
граничные точки (таблица 2.2.1).
Таблица 2.2.1
Вариант |
М |
Вариант |
М |
1 |
|
4 |
|
2 |
|
5 |
|
3 |
|
6 |
|
2.2.2
Для данного множества А
выяснить, является ли множество
![]() открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в
![]() (таблица
2.2.2).
(таблица
2.2.2).
Таблица 2.2.2
Вариант |
|
А |
Вариант |
|
А |
1 |
1 |
|
4 |
|
|
2 |
2 |
|
5 |
3/2 |
|
3 |
2 |
|
6 |
2 |
|
Тема 3
Полнота метрических пространств
2.3.1
Выяснить, является ли последовательность
![]() фундамен-тальной в данном пространстве
X?
Найти
фундамен-тальной в данном пространстве
X?
Найти
![]() ,
если он существует (таблица 2.3.1).
,
если он существует (таблица 2.3.1).
Таблица 2.3.1
Вариант |
X |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
2.3.2
Выяснить, является ли заданное пространство
![]() полным.
полным.
Вариант 1
а) пространство
![]() непрерывно дифференциру-емых на отрезке
непрерывно дифференциру-емых на отрезке
![]() функций с
метрикой
функций с
метрикой
![]() ;
;
б) пространство
всех дважды дифференцируемых на отрезке
функций с
метрикой
![]() .
.
Вариант 2
а) пространство
![]() числовых последовательностей
числовых последовательностей
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
с метрикой
,
с метрикой
![]() ;
;
б) пространство
всех непрерывных на отрезке
функций с
метрикой
 .
.
Вариант 3
а) пространство
![]() всех ограниченных числовых
после-довательностей
с метрикой
всех ограниченных числовых
после-довательностей
с метрикой
![]() ;
;
б)
![]() с метрикой
с метрикой
![]() .
.
Вариант 4
а) пространство
![]() сходящихся к нулю последова-тельностей
с метрикой
сходящихся к нулю последова-тельностей
с метрикой
;
б)
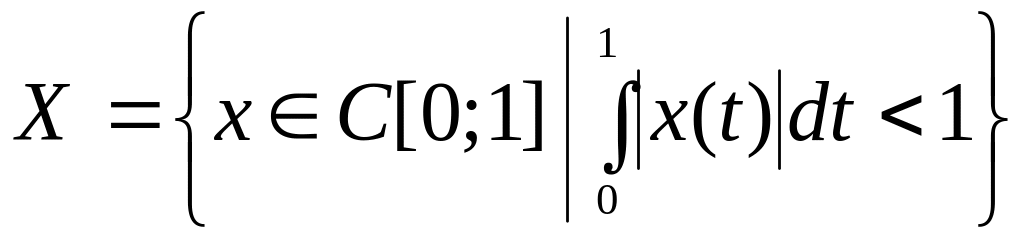 с метрикой
с метрикой
![]() .
.
Вариант 5 а) Пространство с сходящихся последовательностей с метрикой ;
б) с метрикой .
Вариант 6
а) Пространство
![]() ограниченных и непрерывных на интервале
ограниченных и непрерывных на интервале
![]() функций с метрикой
функций с метрикой
![]() ;
;
б)
![]() с метрикой
.
с метрикой
.
Тема 4
Непрерывные отображения
2.4.1
Выяснить,
является ли заданное отображение
![]() на своей естественной области определения
непрерывным в точке
на своей естественной области определения
непрерывным в точке
![]() (таблица 2.4.1)?
(таблица 2.4.1)?
Таблица 2.4.1
Вариант |
X |
Y |
F |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
2.4.2 Является ли заданное отображение : а) непрерыв-ным; б) равномерно непрерывным; в) удовлетворяющим условию Липшица (таблица 2.4.2)?
Таблица 2.4.2
Вариант |
X |
Y |
F |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
Тема 5
Компактные множества в метрических пространствах
2.5.1 Выяснить, является ли множество М предкомпактным, компактным в (таблица 2.5.1).
Таблица 2.5.1
Вариант |
М |
Вариант |
М |
1 |
|
4 |
|
2 |
|
5 |
|
3 |
|
6 |
|
2.5.2
Определить, является ли данное множество
М
предком-пактным в
![]() (таблица
2.5.2)?
(таблица
2.5.2)?![]()
Таблица 2.5.2
Вариант |
р |
М |
1 |
2 |
|
2 |
1 |
|
3 |
2 |
|
4 |
2 |
|
5 |
1 |
|
6 |
1 |
|
Тема 6
Сжимающие отображения
2.6.1 Является
ли отображение F
метрического пространства X
в себя сжимающим? Найти
![]() ,
где
,
где
![]() .
Оценить расстояние от
до неподвижной
точки в случае, если F
является сжимающим (таблица 2.6.1).
.
Оценить расстояние от
до неподвижной
точки в случае, если F
является сжимающим (таблица 2.6.1).
Таблица 2.6.1
Вариант |
X |
F |
1
|
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
2.6.2
Применим ли принцип сжимающих отображений
к заданному интегральному уравнению в
пространстве Х
при
![]()
![]() ?
При
?
При
![]() с точностью до 0,01 найти приближенное
решение и сравнить его с точным решением
(таблица 2.6.2).
с точностью до 0,01 найти приближенное
решение и сравнить его с точным решением
(таблица 2.6.2).
Таблица 2.6.2
Вариант |
Х |
|
|
|
уравнение |
1 |
2 |
3 |
4 |
5 |
6 |
1
|
|
|
|
|
|
Окончание таблицы 2.6.2
1 |
2 |
3 |
4 |
5 |
6 |
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
1 |
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|