2.3. Оценка погрешности

Итак, последовательности чисел , и , вы­численные по формулам (2.2), (2.4) и (2.6) соответственно, являют­ся приближающими для точного значения интеграла , т.е. . Для оценки погрешностей членов этих последовательностей можно использовать два способа.

Аналитическая оценка погрешностей. Известны следующие оценки погрешностей:

для формулы прямоугольников ;

для формулы трапеций ;

для формулы Симпсона .

Используя эти оценки, можно найти минимально необходимое разбиение отрезка , при котором соответствующий элемент приближающей последовательности будет иметь погрешность, не превышающую задан­ной заранее точности .

Например, требуется найти минимальное , при которой приближенное значение интеграла , вычисленное по формуле трапеций, будет иметь погрешность, не превышающую . Находим и решаем неравенство:

, отсюда и . Следовательно, для достижения точности при использовании формулы трапеций надо разбить отрезок на 14 частей и воспользоваться формулой (2.4).

Упражнение 1. Определите такое для данного интеграла для слу­чая формул прямоугольников и Симпсона.

Оценка погрешностей по правилу Рунге. Аналитическая оценка погрешностей часто бывает затрудни­тельной, т.к. возникают проблемы с нахождением максимума модуля нужной производной подынтегральной функции. В связи с этим на практике используют оценку погрешностей по правилу Рунге (кото­рое, вообще говоря, базируется на указанных выше аналитических оценках).

Правило Рунге состоит в следующем. Если - приб­лижающая последовательность для точного значения интеграла, вычисленная по одной из формул: (2.2), (2.4) или (2.6), то погреш­ность элемента оценивается по формуле

, (2.7)

где и - элементы последовательности , вычисленные для разбиения отрезка интегрирования соответственно на и частей, а параметры и определяются из таблицы.

Номер формулы	(2.2)	(2.4)	(2.6)
	3 2	3 2	2 4

Если - заданная заранее точность вычислений, то начальное число разбиений отрезка интегрирования рекомендуется выбирать, исходя из неравенства . Затем вычисляются элементы приближающей последо­вательности , , до тех пор, пока погрешность, определенная по формуле (2.7), не будет меньше .

Следует отметить, что использование правила Рунге увели­чивает количество необходимых вычислений по сравнению с тем, если оценивать погрешность аналитически. Поэтому оно эффектив­но только в случае применения вычислительной техники.

Задания

Задание. 1) Вычислить интеграл по формуле трапеций с точностью до 0,001, определив число разбиений n, используя аналитическую оценку погрешности.

2) Вычислить интеграл, используя формулу Симпсона при и при n = 8. Оценить погрешность результата по правилу Рунге.

№1. 1) 2)

№2. 1) 2)

№3. 1) 2)

№4. 1) 2)

№5. 1) 2)

№6. 1) 2)

№7. 1) 2)

№8. 1) 2)

№9. 1) 2)

№10. 1) 2)

№11. 1) 2)

№12. 1) 2)

№13. 1) 2)

№14. 1) 2)

№15. 1) 2)

№16. 1) 2)

№17 1) 2)

№18 1) 2)

№19 1) 2)

№20 1) 2)

№21 1) 2)

№22 1) 2)

№23 1) 2)

№24 1) 2)

№25 1) 2)

№26 1) 2)

№27 1) 2)

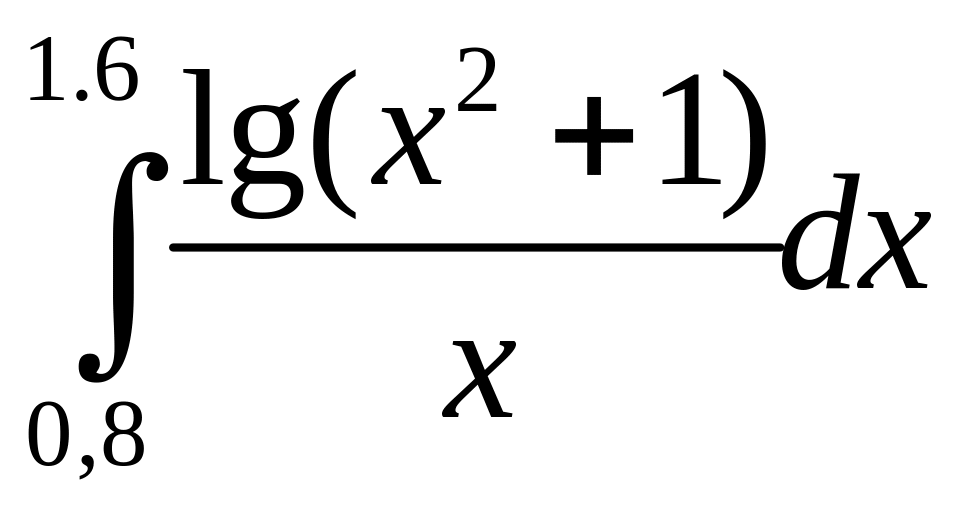
№28 1) 2)

№29 1) 2)

№30 1) 2)