Порядок защиты результатов лабораторных работ

К защите каждым студентом предъявляется полностью оформлен-ный лабораторный отчет, содержащий сверенный с истинным результат и статистическую обработку.

При защите обсуждаются теоретические основы метода, его конкрет-ное воплощение в применяемой методике. Обсуждение ведется в соответ-ствии с контрольными вопросами, предложенными в методических указа-ниях к лабораторной работе.

В программу защиты входит решение расчетной задачи на обсужда-емую тему из типового сборника по курсу ФХМА.

После получения условия задачи и конкретных контрольных вопро-сов студент имеет время в пределах 0,5 ч для решения задачи и подготовки к ответу.

Приложение 2

Статистическая обработка результатов анализа Статистическая обработка градуировочной зависимости

Если градуировочная функция является прямой, выходящей не из начала координат, то градуировочная модель выражается уравнением

где b₀ – сигнал фона; b₁ – коэффициент чувствительности. Коэффициенты b₀ и b₁ можно вычислить методом наименьших квадратов:

,

,

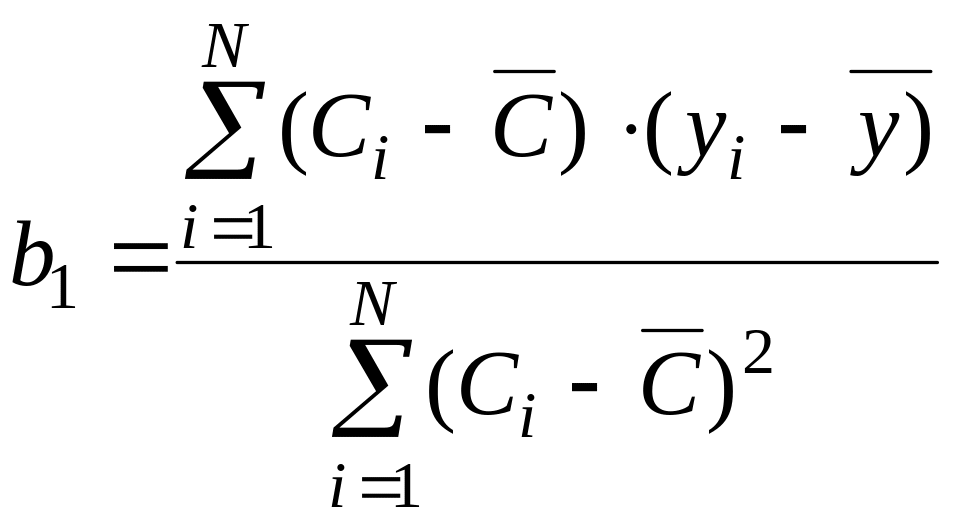где и – средние арифметические из всех значений концентраций (С_i) образцов сравнения, используемых для градуировки, и соответствующих им аналитических сигналов (y_i); N – число образцов сравнения. Качество градуировочной модели можно оценить с помощью остаточного стандарт-ного отклонения:

,

где , а – невязка между экспериментальной и расчетной величинами аналитического сигнала в градуировочной зависи-мости. Величина s_y имеет размерность аналитического сигнала, поэтому удобнее пользоваться стандартным отклонением методики s_c, которое имеет размерность концентрации:

.

Приведенные расчеты справедливы при выполнении условий:

1. Погрешности при приготовлении образцов сравнения значительно меньше погрешностей измерения.

2. Все результаты измерений статистически независимы.

3. Все результаты измерений имеют одно и то же стандартное откло-нение, не зависящее от концентрации и величины аналитического сигнала.

4. Все результаты измерений распределены по нормальному закону.

Очень часто нарушается условие 3. В этом случае при построении градуировочного графика необходимо уменьшить диапазон концентраций или строить градуировочные зависимости раздельно в области малых и больших концентраций.

При выполнении всех условий для определения концентрации вещества можно пользоваться формулой, обратной аналитическому выражению градуировочной модели:

Качество калибровочной модели оценивают путем расчета доверительного интервала:

,

,

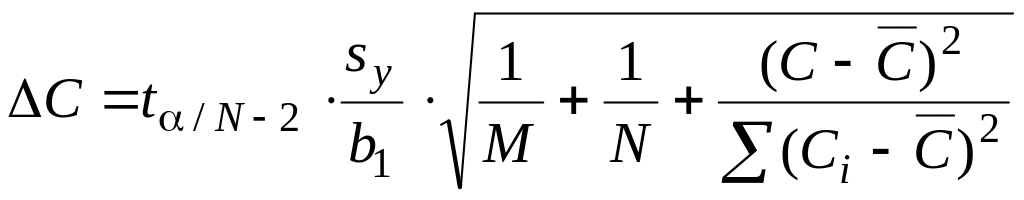где t – коэффициент Стьюдента; – среднее арифметическое из концен-траций всех образцов сравнения; N – число образцов сравнения; М – число параллельных определений данной концентрации.

Пример. Для определения концентрации серебра фотоколориметри-ческим методом построена градуировочная зависимость оптической плот-ности A от концентрации серебра С (мг/см³). Градуировочная зависимость содержит 7 точек, результаты приведены в табл. П.1.

Проведена серия анализов раствора неизвестной концентрации, со-стоящая из трех параллельных определений. Оптические плотности равны: A₁ = 0,522; A₂ = 0,512; A₃ = 0,534. Рассчитать неизвестную концентрацию серебра в растворе, пользуясь градуировочной зависимостью. Определить доверительный интервал для полученной величины.

Решение: = 0,5143; = 0,4569.

Градуировочная зависимость (рис. П.1)

, s_y = 0,0085, s_c = 0,0097 мг/см³.

Таблица П.1

Градуировочная зависимость оптической плотности от концентрации при фотоколориметрическом определении серебра с n-диметиламинобензилиденроданином ( = 450 нм; длина кюветы 1 см; стандартный раствор 1000 мг/см³; рабочий раствор 10 мг/см³)

N	Сi, мг/см3	yi (А)	yрасч
1	0,100	0,086	0,0939	-0,00793	0,153640816	0,171632653	6,29E-05
2	0,300	0,269	0,2691	-0,00013	0,040255102	0,045918367	1,69E-08
3	0,500	0,445	0,4443	0,00067	0,000169388	0,000204082	4,49E-07
4	0,500	0,452	0,4443	0,00767	0,000069389	0,000204082	5,88E-05
5	0,600	0,538	0,5319	0,00607	0,006955102	0,007346939	3,68E-05
6	0,700	0,626	0,6195	0,00647	0,031412245	0,034489796	4,19E-05
7	0,900	0,782	0,7947	-0,01273	0,125412245	0,148775510	1,62E-04
	3,6	3,198			= 0,357914286	= 0,40857143	= 0,000363

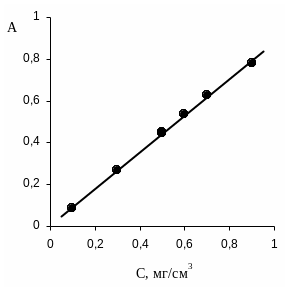
Рис. П.1. Градуировочная зависимость оптической плотности от концентрации

Из серии параллельных = 0,5227, из градуировочной зависимости C = 0,589 мг/см³; = 0,07513.

Используя данные табл. П.2, вычислим доверительный интервал.

Таблица П.2

Данные для расчета доверительного интервала

N
1	0,171633
2	0,045918
3	0,000204
4	0,000204
5	0,007347
6	0,034490
7	0,148776
	0,408571

Из табл. П.3 коэффициент Стьюдента t _{0,95, 2} = 4,30.

0,035 мг/см³.

Таким образом, результат определения концентрации серебра

мг/см³.

Таблица П.3

Коэффициенты Стьюдента

α	n
	2	3	4	5	6	7	8	9	10	15
0,70	2,0	1,3	1,3	1,2	1,2	1,1	1,1	1,1	1,1	1,1
0,95	12,7	4,3	3,2	2,8	2,6	2,4	2,4	2,3	2,3	2,1
0,99	63,7	9,9	5,8	4,6	4,0	3,7	3,5	3,4	3,3	3,0