2.4.Принцип суперпозиции интенсивность волн.

Рассмотрим возмущение, возникающее при одновременном действии двух или нескольких осцилляторов. Простейшая гипотеза , которую можно принять в отношении их совместного действия , заключается в следующем: если и т.д. – возмущения , производимые каждым отдельным осциллятором в какой-либо точке пространства в данный момент времени , а - результирующее возмущение , то

(2.4.1)

Если результирующее движение описывается волновым уравнением , то необходимо , чтобы тоже было решением этого уравнения решения волнового уравнения аддитивны , и следовательно ,(2.4.1) есть решение волнового уравнения . Здесь следует подчеркнуть , что этот математический результат сам по себе не гарантирует , что (2.4.1) точно описывает эффект одновременного действия нескольких волн в данной точке. Принцип суперпозиции есть физическая гипотеза , согласно которой для световых волн возмущение , создающееся при прохождении ряда волн , равно алгебраической сумме возмущений , производимых каждой волной в отдельности. Уравнение (2.4.1) является математической формулировкой этого принципа . Высказанная гипотеза справедлива в той мере , в какой основанные на ней вычисления удовлетворительно описывают соответствующие оптические эксперименты.

При исследовании звуковых волн было найдено , что для волн большой амплитуды скорость распространения зависит от их амплитуды .Было так же установлено , что при одновременной работе двух громких источников звука разной частоты слышны их суммовой и разностный тона. Для описания таких явлений необходимо предположить , что простая форма волн не точно передает свойства звуковых волн конечной амплитуды и что возмущение , возникающее при одновременном действии двух источников звука, дается соотношением

(2.4.2)

где - константы , малые по сравнению с .

Подобные гипотезы потребовалось бы ввести , если бы соответствующие явления наблюдались и при исследовании света; однако до сих пор все попытки обнаружить такие эффекты давали отрицательные результаты. Шредингер рассмотрел результаты , получающиеся при введении некоторых нелинейных членов (вида, предложенного Борном) в уравнении распространении электромагнитных волн. Расчеты показали , что при очень больших интенсивностях скорость света должна зависеть от

Амплитуды, но в практически осуществимых условиях эффект слишком мал, чтобы его можно было наблюдать на опыте.

2.5.Закон отражения и преломления в электромагнитной теории света.

Когда луч достигает плоской границы раздела двух прозрачных сред , он частично проходит во вторую среду (преломляется), частично возвращается обратно (отражается).Закон отражения света был известен еще грекам. Он утверждал , что падающий и отраженный лучи лежат в одной плоскости с нормалью к границе раздела в точке падения ( эта плоскость называется плоскостью падения), причем угол падения равен углу отражения . (рис. 2.5.1)

Рис. 2.5.1.

Закон преломления был установлен экспериментально в 1621 г. голландским ученым Снеллиусом (1580-1626) и опубликован только после его смерти. Позднее Декарт (1596-1650) в 1637 г. опубликовал тот же закон , не ссылаясь на Снеллиуса. Знал ли Декарт работы Снеллиуса – этот вопрос остался открытым , хотя он и был предметом многочисленных дискуссий . Декарт получил закон преломления Снеллиуса , пользуюсь аналогией между преломлением света и прохождением упругого шара ( мяча)через границу раздела воздух с водой . Его рассуждения были неубедительны и крайне туманны , но окончательный результат , к которому он пришел , оказался верным.

Согласно закону преломления Снеллиуса , преломленный луч лежит в плоскости падения , причем отношение синуса угла падения (рис 2.5.2) к синуса угла преломления для рассматриваемых сред зависит только от длины световой волны , но не зависит от угла падения , т.е. (2.5.1)

Рис. 2.5.2.

Постоянная величина называется относительным показателем или коэффициентом преломления второй среды относительно первой . Показатель преломления среды относительно вакуума называют абсолютным показателем ( коэффициентом ) преломления этой среды. Его будем обозначать через n, снабжая эту букву если требуется , соответствующими индексами . Например , - показатель преломления первой , а - второй сред . Ради кратности величину n обычно называют просто показателем (коэффициентом ) среды, т.е. опускают прилагательное «абсолютный».

Относительный показатель преломления выражается через абсолютные показатели и соотношением (2.5.2)

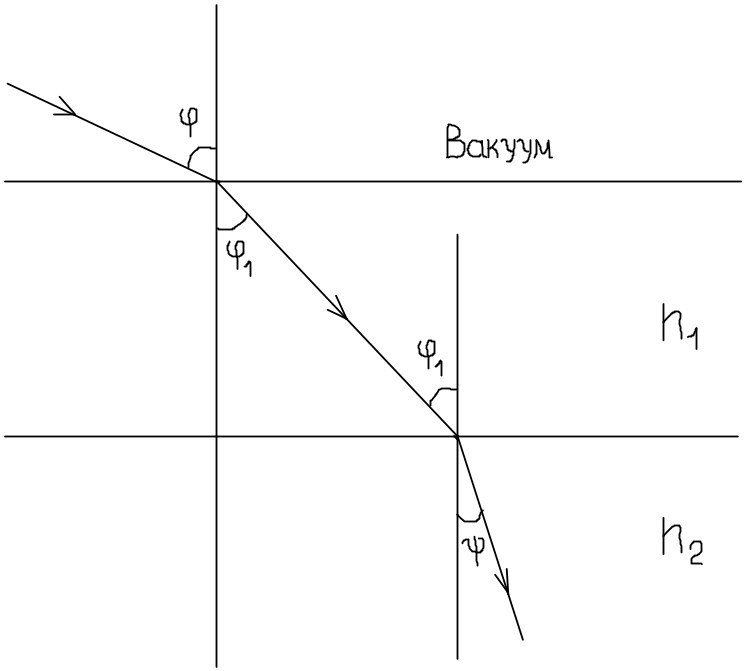
Рис.2.5.3

Это соотношение можно получить путем предельного перехода . Пусть световой луч падает из вакуума на плоскопараллельную пластинку с показателем преломления , а затем попадает в среду с показателем преломления (рис.2.5.3)

Для преломления на границах пластинки можно написать ,

Перемножая написанные равенства , получим (2.5.3)

Это соотношение справедливо , какова бы ни была толщина пластинки . Оно остается верным и в предельном случае , когда толщина пластинки стремится к нулю . Но тогда свет будет преломляться так, как если бы ни какой пластинки вообще не было . Поэтому должно быть Сравнение этого результата с предыдущим и приводит к соотношению (2.5.2)

Слабая сторона приведенного рассуждения состоит в следующем. Показатель преломления есть макроскопическая характеристика среды .Когда толщина пластинки , разделяющей среды 1 и 2 , становится порядка атомных размеров, ее уже нельзя рассматривать как непрерывную среду , так что понятие показателя преломления теряет смысл .Однако окончательный результат (2.5.2) остается верным .Он подтверждается опытом и в дальнейшем при рассмотрении теории отражения и преломления света будет выведен с различных точек зрения .

С учетом соотношения (2.5.2) закон преломления можно записать в симметричной форме:

. (2.5.4)

из формулы (2.5.2) следует также :

. (2.5.5)