МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра ДВС

Отчёт по курсовой работе

по дисциплине “Информатика”

Выполнил: студентка гр. Т27Д-216

Ахметханов Р.А.

Принял: доц. каф. ДВС

Рудой И.Б.

Уфа 2006

1. Тексты заданий

1. Написать программу для решения уравнения методом касательных.

2. Написать программу для интегрирования методом Симпсона.

3. Написать программу для нахождения коэффициентов аппроксимацион-ного многочлена методом наименьших квадратов.

4. Написать программу для решения дифференциального уравнения методом Рунге-Кутта.

5. Написать программу для нахождения минимума (максимума) целевой функции методом покоординатного спуска.

2. Тексты исходных кодов программ

2.1 Метод касательных.

//Метод касательных

double kasat(double x)

{

return log(x-7)+4*sin(x);

}

double dkasat(double x)

{

return 1/(x-7)+4*cos(x);

}

void __fastcall TForm1::Button2Click(TObject *Sender)

{

double c, x, E=0.01;

c=10;

do

{

x=c;

c=x-kasat(x)/dkasat(x);

}

while(fabs(kasat(c))>E);

Memo1->Lines->Add("x="+FloatToStr(c));

}

2.2 Метод Симпсона.

// Метод Симпсона

double INTEGRAL(double x)

{

return log(x+2)/log10(x-2)+cos(4*x);

}

void __fastcall TForm1::Button3Click(TObject *Sender)

{

double a=30, // интервал

b=50, // определённого интеграла

E=0.01, // точность

S,

K1=0, K2, h; // шаг

double X[3];

int i, n=4;

h=(b-a)/4;

for (int j=0; j<17; j++)

{

K2=0;

for(i=2; i<n;i+=2)

{

X[2]=a+i*h;

X[1]=X[2]-h;

X[0]=X[1]-h;

S=INTEGRAL(X[0])+4*INTEGRAL(X[1])+INTEGRAL(X[2]);

K2+=S;

}

K2*=h/3;

if(fabs(K1-K2)<E) break;

else

{

K1=K2;

n*=2;

h/=2;

}

}

Memo1->Lines->Add(FloatToStr(fabs(K2)));

}

2.3 Метод наименьших квадратов.

{ const int n=7, //порядок многочлена

m=8; //количество узлов интерполяции

int i, j, k;

float a[n+1][n+1]={0}, // коэффициенты СЛУ

b[n+1]={0}, // значения СЛУ

X[8]={5,6,9,10,11,14,15,19},

y[8]={2,12,3,10,5,-4,-5,2},

x[6]={0}; // искомые коэффициенты

// нахождение коэффициентов СЛУ (метод наименьших квадратов)

for (i=0; i<=n; i++)

{

for (j=i; j<=n; j++)

{

for (k=0; k<m; k++)

{

if (X[k]!=0)

{

a[i][j]+=pow(X[k],(i+j));

if (i!=j) a[j][i]=a[i][j];

}

}

}

}

for(i=0; i<=n; i++)

{

for(k=0; k<m; k++)

{

if(X[k]!=0) b[i]+=pow(X[k],i)*y[k];

}

}

// Решение СЛУ методом Гаусса

float temp;

// Прямой ход метода Гаусса

for(k=0; k<=n-1; k++)

{

for (i=k+1;i<=n; i++)

{

temp=a[i][k]/a[k][k];

a[i][k]=0;

for(j=k+1;j<=n; j++)

{

a[i][j]=a[i][j]-temp*a[k][j];

}

b[i]=b[i]-temp*b[k];

}

}

x[n]=b[n]/a[n][n];

//Обратный ход метода Гаусса

for(i=n-1; i>=0; i--)

{

temp=0;

for(j=i+1; j<=n; j++)

{

temp=temp+a[i][j]*x[j];

}

x[i]=(b[i]-temp)/a[i][i];

}

// Печать результата

for(i=0; i<=n; i++)

{

Memo1->Lines->Add("a["+IntToStr(i)+"]="+FloatToStr(x[i]));

}

}

2.4 Метод Рунге-Кутта.

double Runge(double x, double y, double y1)

{

return 8*x*x-y1*exp(0.5*x);

}

void __fastcall TForm1::Button5Click(TObject *Sender)

{

Panel1->Visible=false;

Panel2->Visible=false;

Panel3->Visible=false;

Panel4->Visible=false;

Panel5->Visible=true;

Panel6->Visible=false;

Label1->Caption="дифференциальное уравнение:";

Label2->Caption="Функция, определённая таблицей:";

Memo1->Clear();

double x=-1.3,

y=3.6,

y1=2.5,

h=1;

double k0, k1, k2, k3;

double p0, p1, p2, p3;

int n=8;

for (int i=1;i<=n;i++)

{

k0=Runge(x,y,y1);

p0=Runge(x,y,y1);

k1=Runge(x+h/2,y+k0/2,y1+p0/2);

p1=Runge(x+h/2,y+k0/2,y1+p0/2);

k2=Runge(x+h/2,y+k1/2,y1+p1/2);

p2=Runge(x+h/2,y+k1/2,y1+p1/2);

k3=Runge(x+h,y+k2,y1+p2);

p3=Runge(x+h,y+k2,y1+p2);

y+=h/6*(k0+2*k1+2*k2+k3);

y1+=h/6*(p0+2*p1+2*p2+p3);

x+=h;

Memo1->Lines->Add("x="+FloatToStr(x)+" y="+FloatToStrF(y, ffFixed, 8, 3));

}

}

2.5 Метод покоординатного спуска.

float x[2]; // глобальный массив параметров

float GoldSection( int);

float function(float, int);

void __fastcall TForm1::Button6Click(TObject *Sender)

{

float A, B,

E=0.001;

int i;

x[0]=4;// начальные

x[1]=6;// приближения

B=log(x[0]+2)/log10(x[0]-2)+cos(4*x[0])+pow(x[1],2)-log(x[1]);

// цикл поиска оптимальных параметров

do

{

i=0;

A=B;

for(; i<2; i++)

{

// фиксируется параметр x[1]

if(i==0)

{

x[0]=GoldSection(i);

}

// фиксируется параметр x[0]

if(i==1)

{

x[1]=GoldSection(i);

}

}

B=log(x[0]+2)/log10(x[0]-2)+cos(4*x[0])+pow(x[1],2)-log(x[1]);

}

while (fabs(A-B)>E);

Memo1->Lines->Add("Оптимальные значения параметров:");

Memo1->Lines->Add(" x="+FloatToStr(x[0]));

Memo1->Lines->Add(" z="+FloatToStr(x[1]));

Memo1->Lines->Add("Минимальное значение функции:");

Memo1->Lines->Add(" " +FloatToStr(B));

}

// Метод золотого сечения

float GoldSection(int i)

{

float a=30, b=50,

y,z,

A, B,

E=0.001;

if (i==1) a=0.001;

y=0.618*a+0.382*b;

z=0.382*a+0.618*b;

A=function(y, i);

B=function(z, i);

while(1)

{

if(A<B)

{

b=z;

if((b-a)<E) break;

else

{

z=y;

B=A;

y=0.618*a+0.382*b;

A=function(y,i);

}

}

else

{

a=y;

if((b-a)<E) break;

else

{

y=z;

A=B;

z=0.382*a+0.618*b;

B=function(z, i);

}

}

}

return (a+b)/2;

}

// Целевая функция

float function(float X, int i)

{

float y;

// Фиксируется параметр x[1]

if(i==0) y=log(X+2)/log10(X-2)+cos(4*X)+pow(x[1],2)-log(x[1]);

// Фиксируется параметр x[0]

if(i==1) y=log(x[0]+2)/log10(x[0]-2)+cos(4*x[0])+pow(X,2)-log(X);

return y;

}

3. Исходные данные

1. Уравнение:

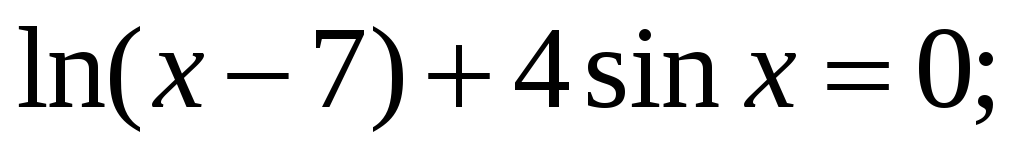
2. Функция для интегрирования:

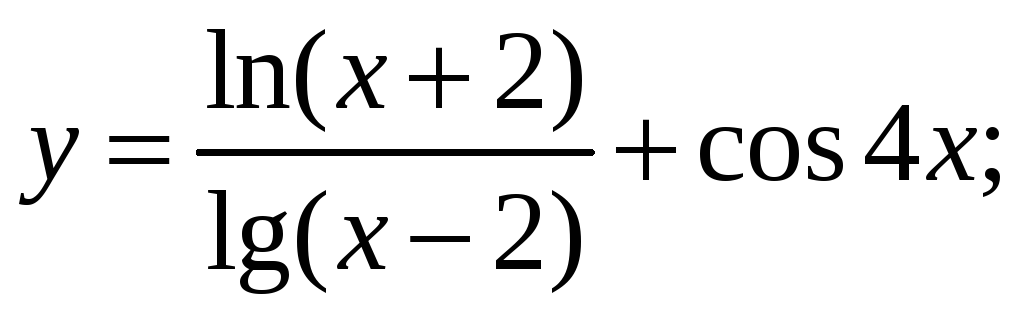
Интервал интегрирования:

3. Функция, заданная таблицей:

x	5	6	9	10	11	14	15	19
y	2	12	3	10	5	-4	-5	2

Порядок аппроксимационного многочлена: 7.

4. Дифференциальное уравнение:

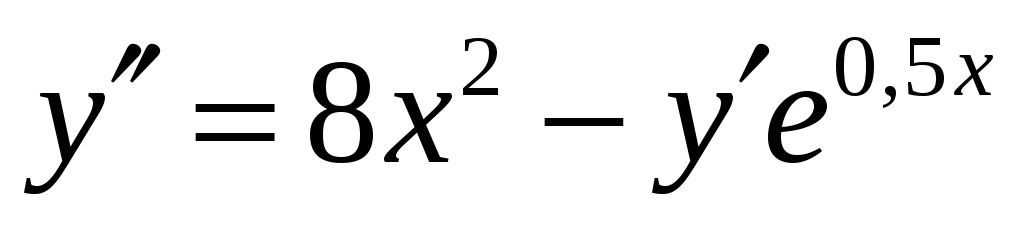
Начальные условия: x₀ = -1,3 ; y₀ =3,6; y’₀ = 2,5 .

5. Целевая функция:

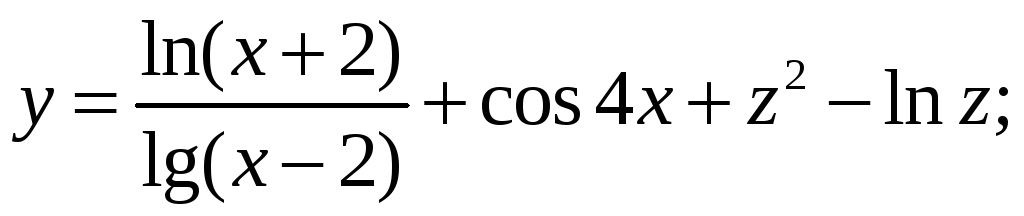
Интервал поиска: .

4. Полученные результаты.

4.1 Решение уравнения: x=9,67304164963966;

4.2 Интеграл равен 46,9908189947402;

4.3 Коэффициенты аппроксимационного многочлена:

a[0]=-177,323364257813

a[1]=71,9839477539063

a[2]=-8,87602615356445

a[3]=0,334429979324341

a[4]=-0,00613873777911067

a[5]=0,00243691960349679

a[6]=-0,000219567038584501

a[7]=5,38973336006165E-6

4.4 Функция, определенная таблицей:

x	y
-0,3	5,87594713422359
0,7	3,49136924298238
1,7	8,66681792972679
2,7	15,7441042009337
3,7	22,3071040263055
4,7	492,279605237451
5,7	488190,027025295
6,7	4133156477,17784

4.5 Оптимальные значения проектных параметров:

x=46,3387145996094

z=0,707228004932404

Минимальное значение функции:

2,20160961151123