Розділ 3.Розв’язок диференційних рівнянь

3.1Розв’язок диференційних рівнянь методом Ейлера

Метод Ейлера є дуже простим способом знаходження наближеного розв’язку задачі Коші.

Нехай ми маємо наступну інформацію:

x' = f(x, t),

x(t₀) = x₀.

графічна інтерпретація метода наступна:

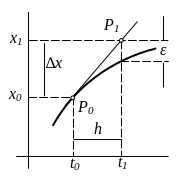
В точці t₀ будуємо дотичну, графік якої і буде апроксимацією шуканої інтегральної кривої, у даному випадку до точки t₁. Очевидно, що чим більший крок h = t₁ – t₀, тим більше буде віддалятися дотична від точного розв'язку.

Значення x(t₁) = x₁ в точці P₁ можна порахувати, використавши значення про похідну:

x₁ = x₀ + ∆x = x₀ + h∙tg(α) = x₀ + h∙f(x₀, t₀)

Тут α – це кут нахилу дотичної. Очевидно, що похибка такого розв’язку дорівнює ε.

Для методу Ейлера отриманий розв’язок відрізняється від точного значення х^* на похибку, пропорційну кроку обчислення h в степені p=2, а саме:.

х₁ = х^* + а₁h²+ a₂h³ +….

. Більшої точності можна досягти, зокрема, використовуючи так звану екстраполяцію Річардсона, якщо провести розрахунки двічі з різними кроками h і qh і з отриманих рівнянь знайти точний розв’язок задачі навіть при значних за розміром кроках обчислень:

х^* = х(h) + + 0( ).

З отриманої формули випливає дуже важливе співвідношення для уточнення оцінки глобальної похибки обчислень через різницю двох приблизних розв’язків з урахуванням порядку p=1 використаного методу:Ейлера:

 = х^* - х(h) = .

Якщо крок змінювати в два рази , тобто вибрати q=2, то з отриманих двох неточних рішень х(h) і x(2h) отримаемо більш точне значення

х = х(h) + [ х(h) – x(2h)]/3,

похибка якого визначається кроку обчислення h в третій степені, як у методів другого порядку ( наприклад, методу трапецій).

3.1.1Завдання: виконати один крок метода Ейлера з екстраполяцію Річардсона для диференційного рівняння

Дано задачу Коші:

x' = f(x, t) = t²+3t–4x

для

t₀ = –0.2

h = 0.1

x(–0.2) = 0.100000

Розв'яжемо рівняння відповідно до формули

x_i+1 = x_i + h∙f(x_i, t_i)

Для функції x' = t²+3t–4x маємо:

f(x₀, t₀) = f(0.1, –0.2) = –0.9600

x₁(h) = x₀ + h∙f(x₀, t₀) = 0.1 + 0.1 ∙ (–0.9600) = 0.0040

x₁ (2h)= x₀ + 2h∙f(x₀, t₀) = 0.1 + 0.2 ∙ (–0.9600) = –0.0920

х₁ = х(h) + [ х(h) – x(2h)]/3= 0.0040+ 0.032 = 0.036

Відповідь:

x(0.1) = 0.0360

3.1.2Завдання для самостійної роботи

Завдання № 1

x' = t^2+3.6*t+2.8*x

для

t0 = 0.1

h = 0.10

x(0.1) = -0.100000

Завдання № 2

x' = t^2+4.1*t-4.9*x

для

t0 = -0.2

h = 0.06

x(-0.2) = 0.000000

Завдання № 3

x' = t^2+2.4*t-2.7*x

для

t0 = 0.1

h = 0.06

x(0.1) = 0.000000

Завдання № 4

x' = t^2+4.3*t+5.4*x

для

t0 = 0.1

h = 0.10

x(0.1) = -0.200000

Завдання № 5

x' = -t^2+3.2*t+4.9*x

для

t0 = -0.2

h = 0.06

x(-0.2) = -0.100000

Завдання № 6

x' = t^2-1.3*t-4.3*x

для

t0 = -0.1

h = 0.04

x(-0.1) = 0.000000

Завдання № 7

x' = t^2-4.2*t-4.2*x

для

t0 = 0.0

h = 0.04

x(0.0) = -0.100000

Завдання № 8

x' = t^2+4.7*t+5.2*x

для

t0 = -0.1

h = 0.04

x(-0.1) = -0.100000

Завдання № 9

x' = t^2-1.9*t+1.1*x

для

t0 = -0.1

h = 0.06

x(-0.1) = 0.000000

Завдання № 10

x' = -t^2+5.9*t+1.2*x

для

t0 = -0.1

h = 0.08

x(-0.1) = -0.100000

Завдання № 11

x' = -t^2+1.2*t-2.7*x

для

t0 = -0.1

h = 0.04

x(-0.1) = 0.100000

Завдання № 12

x' = -t^2+4.3*t+4.5*x

для

t0 = -0.1

h = 0.10

x(-0.1) = -0.100000

Завдання № 13

x' = t^2-3.2*t+2.9*x

для

t0 = -0.1

h = 0.08

x(-0.1) = -0.100000

Завдання № 14

x' = -t^2-1.1*t+3.5*x

для

t0 = -0.1

h = 0.10

x(-0.1) = 0.000000

Завдання № 15

x' = -t^2+1.1*t+3.4*x

для

t0 = -0.1

h = 0.10

x(-0.1) = 0.100000

Завдання № 16

x' = -t^2-4.9*t-1.6*x

для

t0 = 0.0

h = 0.04

x(0.0) = -0.100000

Завдання № 17

x' = -t^2+1.3*t-3.7*x

для

t0 = -0.1

h = 0.10

x(-0.1) = -0.100000

Завдання № 18

x' = -t^2-1.9*t-2.9*x

для

t0 = -0.1

h = 0.04

x(-0.1) = -0.100000

Завдання № 19

x' = t^2-2.8*t+4.6*x

для

t0 = -0.2

h = 0.06

x(-0.2) = 0.000000

Завдання № 20

x' = t^2+4.2*t-3.9*x

для

t0 = 0.0

h = 0.04

x(0.0) = 0.100000

Завдання № 21

x' = -t^2-3.5*t-4.6*x

для

t0 = -0.2

h = 0.04

x(-0.2) = 0.000000

Завдання № 22

x' = -t^2-3.1*t+3.1*x

для

t0 = 0.1

h = 0.10

x(0.1) = 0.000000

Завдання № 23

x' = t^2+1.4*t+5.7*x

для

t0 = -0.1

h = 0.06

x(-0.1) = -0.200000

Завдання № 24

x' = t^2-3.6*t+3.4*x

для

t0 = -0.2

h = 0.06

x(-0.2) = -0.100000

Завдання № 25

x' = t^2-5.6*t-2.3*x

для

t0 = 0.0

h = 0.08

x(0.0) = -0.200000

Завдання № 26

x' = t^2-5.8*t+3.5*x

для

t0 = 0.0

h = 0.08

x(0.0) = 0.100000

Завдання № 27

x' = -t^2-2.3*t+2.3*x

для

t0 = 0.0

h = 0.08

x(0.0) = 0.000000

Завдання № 28

x' = t^2-4.7*t+2.6*x

для

t0 = 0.1

h = 0.06

x(0.1) = -0.100000

Завдання № 29

x' = t^2-3.4*t+4.8*x

для

t0 = -0.2

h = 0.04

x(-0.2) = 0.000000

Завдання № 30

x' = -t^2-3.1*t-4.6*x

для

t0 = 0.0

h = 0.06

x(0.0) = -0.100000