
- •«Системы счисления»
- •Практическая работа №1 Системы счисления
- •Лабораторная работа №1. Системы счисления Основы информатики Индивидуальный вариант
- •Решение
- •Задача 4. Выполнить вычитание. Решение
- •Задача 6. Используя схему быстрого перевода, переведите в 2-ю, 8-ю и 16-ю системы заданные десятичные числа. Решение
- •Задача 5. Выполнить умножение. Решение
- •Задача 7. Определить наименьшие основания позиционных систем счисления, при которых истинно заданное равенство. Решение
Задача 5. Выполнить умножение. Решение
А) 11001102*1011112 = 10010101110102

 1
1 0 0 1 1 0
1
1 0 0 1 1 0
 1
0 1 1 1 1
1
0 1 1 1 1
1 1 0 0 1 1 0
1 1 0 0 1 1 0
1 1 0 0 1 1 0
1 1 0 0 1 1 0
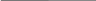 1
1 0 0 1 1 0
1
1 0 0 1 1 0
1 0 0 1 0 1 0 1 1 1 0 1 0
Б) 1272,38 * 23,148 = 32130,0448
2 7 2, 3
2 3, 1 4
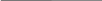 8
(28) 8 (12)
8
(28) 8 (12)
2 7 2, 3
6 (21) 6 9
 4
(14) 4 6
4
(14) 4 6
4 (20)(27)(27)(39)(11)(12) ( /8)
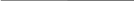 (12)
4
(12)
4
(40) 4 4
 (32)
0 4 4
(32)
0 4 4
(35) 0 0 4 4
 (25)
3 0 0 4 4
(25)
3 0 0 4 4
(10)1 3 0 0 4 4
3 2 1 3 0, 0 4 4
В) 48,416 * 5,А16 = 196.6816

 4
8, 4
4
8, 4
 5,
(10)
5,
(10)
(40) (80) (40)
 (20)(40)
(20)
(20)(40)
(20)
(20)(80)(100)(40) (/16)
 (102)
8
(102)
8
(86) 6 8
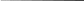 (25)
6 6 8
(25)
6 6 8
1 9 6, 6 8
Задача 7. Определить наименьшие основания позиционных систем счисления, при которых истинно заданное равенство. Решение
120х = 168у 12012=16810
1) Запишем числа в виде многочленов:
120x = 2·x2 + 2 ·x1 +0 и 168y = 1·y2 + 6 ·y1+8
2) Получаем равенство:
2х2+2х=y2+6y+8
3) Преобразуем равенство:
2х(x+1) = y2+6y+8
4) При этом имеем еще 2 ограничения, так как основание системы
счисления должно быть больше самой большой цифры в записи числа:
Х > 3 и Y > 9.
5) В итоге система ограничений следующая:
2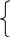 x(x+1)
= y2+6y+8
x(x+1)
= y2+6y+8
Х > 3
Y > 9.
Теперь найдем значения X и Y, удовлетворяющие всем трем условиям.
Для этого, перебирая значения Y>9 по возрастанию, находим такое X,
при котором Y целое положительное число:
Пусть Y = 10: 2х(х+1)=102+6*10+8 =168- Удавлетворяет условию
П усть х=12: тогда 12012 1*122+2*12=144+24=16810 –Удавлетворяет условию
Ответ: 12012=16810
