
- •Программа дисциплины
- •Тема 1 общая характеристика и классификация математических методов и моделей, применяемых в экономических исследованиях Предмет математического программирования
- •Общая схема формирования экономико-математической модели
- •Классификация методов математического программирования
- •Тема 2 линейное программирование Задача линейного программирования (злп)
- •Формы записи задач линейного программирования
- •Приемы, позволяющие переходить от одной формы записи условий задач к другой
- •Графический метод решения злп
- •Симплекс-метод решения злп
- •Алгоритм симплекс-метода
- •Геометрическая интерпретация в случае двух переменных
- •Отыскание начального опорного плана (1-ый пункт алгоритма)
- •Отыскание начального опорного плана методом искусственного базиса
- •Отыскание начального опорного плана путем преобразования таблицы Жордана
- •Шаг Жордановых исключений осуществляется по следующим правилам:
- •Исследование на оптимальность опорного плана при минимизации целевой функции (второй пункт алгоритма)
- •Переход к новому, нехудшему опорному плану (третий пункт алгоритма)
- •Тема 3 транспортная задача линейного программирования Постановка транспортной задачи по критерию стоимости в матричной форме
- •Закрытая и открытая модели транспортной задачи
- •Алгоритм решения сбалансированной транспортной задачи
- •Построение исходного опорного плана (первый пункт алгоритма)
- •Проверка на оптимальность невырожденного опорного плана методом потенциалов (второй пункт алгоритма)
- •Переход к нехудшему опорному плану (третий пункт алгоритма)
- •Цикл пересчета
- •Тема 4 динамическое программирование
- •I этап. Условная оптимизация
- •II этап. Безусловная оптимизация
- •Задача об оптимальной стратегии замены оборудования
- •I этап. Условная оптимизация
- •II этап. Безусловная оптимизация
- •Литература
- •Тема 1 общая характеристика и классификация математических методов и моделей, применяемых в экономических исследованиях 3
- •Тема 2 линейное программирование 6
- •Тема 3 транспортная задача линейного программирования 33
- •Тема 4 динамическое программирование 50
Графический метод решения злп
Графическим методом
можно решать любые задачи линейного
программирования (ЗЛП) с двумя переменными
(![]() =2),
а также ЗЛП с
>2
переменными, если в ее канонической
записи число неизвестных
и число линейно независимых уравнений
=2),
а также ЗЛП с
>2
переменными, если в ее канонической
записи число неизвестных
и число линейно независимых уравнений
![]() связаны соотношением
связаны соотношением
![]() .
.
Пример 6
Решим графически задачу ЛП, экономико-математическая модель которой составлена в примере 3.
![]() ;
;
![]() (2.10)
(2.10)
Вначале построим
многоугольник решений или ОДР задачи
(рисунок 1). Для этого в системе координат
![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, например начала координат. Ограничения (2.10) означают, что ОДР лежит в I четверти системы координат . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет многоугольник решений данной задачи (ОДР).
Для того чтобы
построить прямую
![]() ,
строим направляющий вектор
,
строим направляющий вектор
![]() ,
который перпендикулярен прямой Z.
Прямая, проходящая через начало координат
и перпендикулярная вектору
,
который перпендикулярен прямой Z.
Прямая, проходящая через начало координат
и перпендикулярная вектору
![]() ,
и будет прямая
,
и будет прямая
![]() .
Затем прямую
перемещаем параллельно самой себе в
направлении вектора N
по
многоугольнику решений (ОДР) (рисунок
1). Последняя точка соприкосновения
прямой
с ОДР и есть оптимальное решение.
.
Затем прямую
перемещаем параллельно самой себе в
направлении вектора N
по
многоугольнику решений (ОДР) (рисунок
1). Последняя точка соприкосновения
прямой
с ОДР и есть оптимальное решение.

Рисунок 1
Вектор
![]() указывает направление возрастания
целевой функции Z.
Оптимальное решение ЗЛП может достигаться
лишь в точках, принадлежащих границе
многоугольника решений. В нашем примере,
как видно из рисунка 1, функция Z
принимает максимальное значение в точке
указывает направление возрастания
целевой функции Z.
Оптимальное решение ЗЛП может достигаться
лишь в точках, принадлежащих границе
многоугольника решений. В нашем примере,
как видно из рисунка 1, функция Z
принимает максимальное значение в точке
![]() .
Точка
лежит на пересечении прямых
.
Точка
лежит на пересечении прямых
![]() и
и
![]() .
Для определения ее координат необходимо
решить систему уравнений:
.
Для определения ее координат необходимо
решить систему уравнений:
![]()
Откуда
![]() .
Это и есть оптимальный план задачи.
Подставив значение
и
в целевую функцию Z,
получаем
.
Это и есть оптимальный план задачи.
Подставив значение
и
в целевую функцию Z,
получаем
![]() .
.
Таким образом, для того чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
Симплекс-метод решения злп
Особенностью задач ЛП является то, что целевая функция достигает экстремума на границе области допустимых решений (ОДР).
Допустимый план, принадлежащий границе ОДР, называется опорным планом.
Алгоритм симплекс-метода
Находим какой-либо начальный опорный план
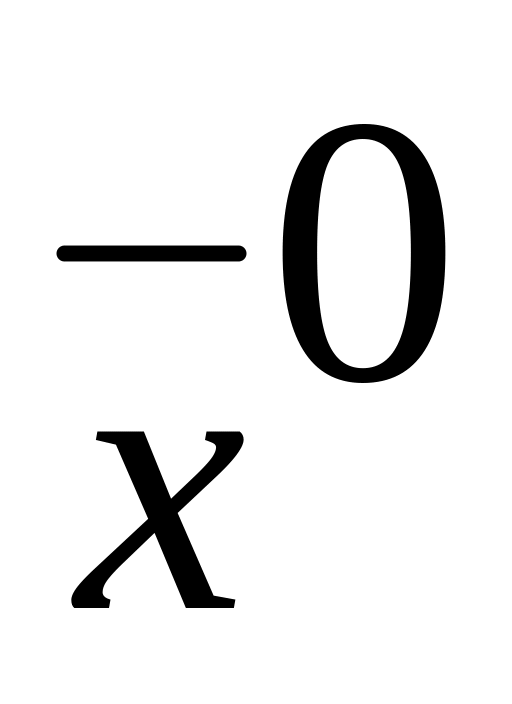 .
.Проверяем его на оптимальность. Если план оптимален, то задача решена, иначе переходим к пункту 3.
По правилам преобразования таблицы Жордана переходим к нехудшему опорному плану. Переходим к пункту 2.
С геометрической
точки зрения перебор опорных планов
можно толковать как переход по ребрам
из одной вершины многогранника планов
(области допустимых решений) в другую,
по направлению к вершине
![]() ,
в которой целевая функция достигает
экстремального значения.
,
в которой целевая функция достигает
экстремального значения.
Геометрическая интерпретация в случае двух переменных
![]()
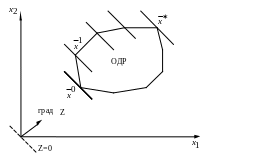
Отыскание начального опорного плана (1-ый пункт алгоритма)
Пусть система ограничений ЗЛП представлена в канонической форме записи:
![]()
![]()
![]() .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательности правой части ( ) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю.
Например, в системе ограничений
![]()
первое и второе ограничения имеют предпочтительный вид, а третье – нет (предпочтительные переменные подчеркнуты).
Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные – свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам.
Например, в системе ограничений:
![]()
предпочтительными
(базисными) являются переменные
![]() свободными – переменные
свободными – переменные
![]() .
.
Приравниваем
свободные переменные
к нулю, тогда базисные переменные примут
значения:
![]() ,
,
![]() ,
,
![]() .
.
Получим начальный
опорный план
![]() .
.
