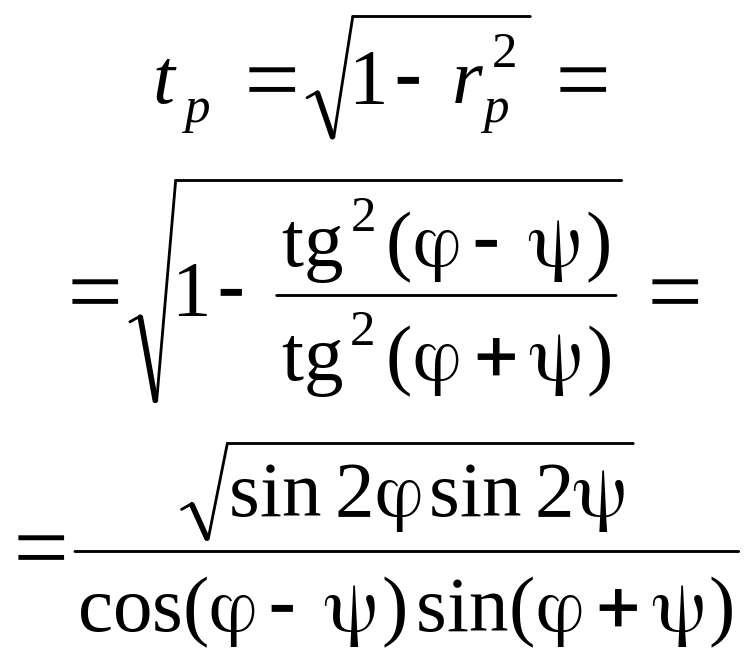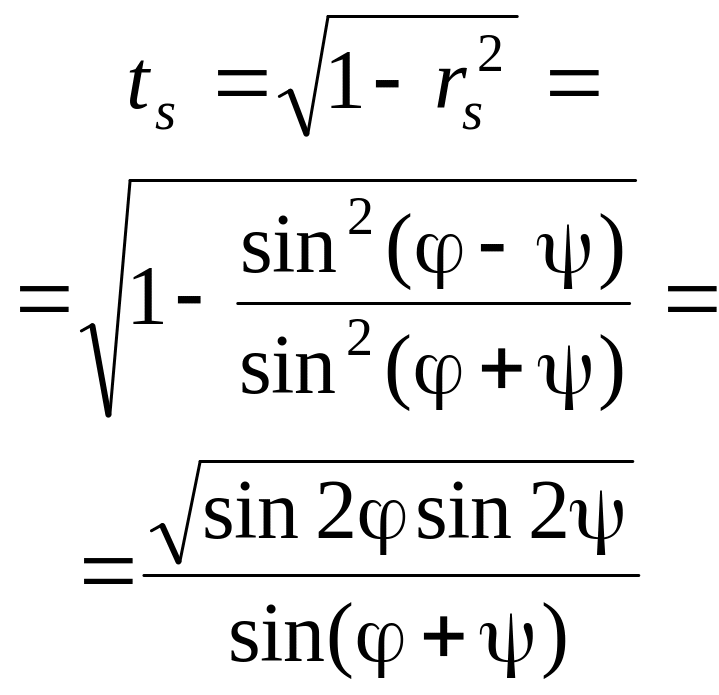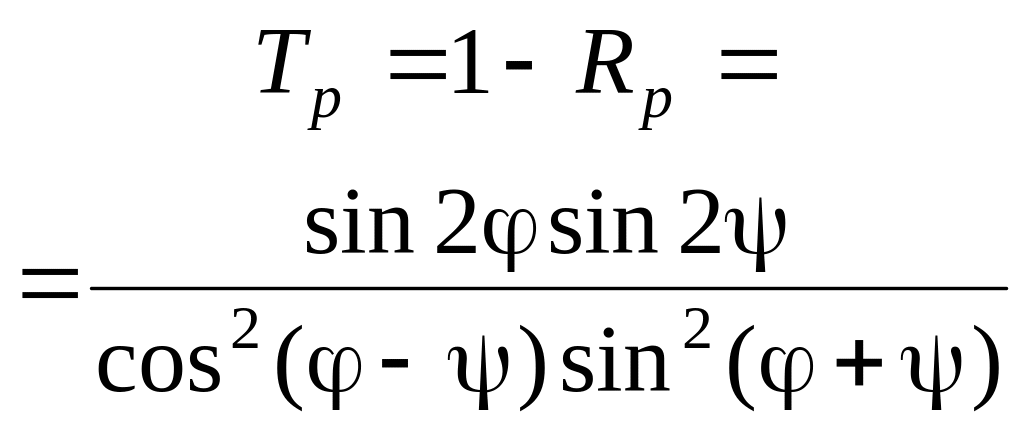13. Особенности отражения и преломления свет на границе раздела двух изотропных, однородных, диэлектрических сред.

Одним из следствий поляризации излучения является френелевское отражение поляризованного излучения от диэлектрической границы изотропных и однородных сред. Важность этого эффекта состоит не только в необходимости учета его особенностей, но и выявлении эффективных механизмов управления этими процессами с целью практической реализации уникальных возможностей.

Впервые теорию этого процесса построил Френель, основываясь на важнейших балансовых соотношениях. Важнейшим таким соотношением является соотношение из закона Снеллиуса о том, что касательная составляющая лучевого вектора не претерпевает разрыва при похождении через диэлектрическую границу раздела сред.

Рассматриваются два случая ориентации плоскости поляризации линейно поляризованного излучения. Первый – когда плоскость поляризации совпадает с плоскостью падения луча (p-поляризация или ||-случай), и второй – плоскость поляризации ортогональна плоскости падения (s-поляризация или -случай).

На рисунке ниже представлен ход лучей и заданная система координат при преломлении и отражении излучения от границы раздела диэлектрических сред. Там же показана трехмерная система координат, в которой позиционируются вектора и их проекции. Пространственная ориентация электрического вектора соответствует случаю p-поляризации излучения.

Для вывода основных соотношений необходимо рассмотрение всех проекций как электрического вектора, так и магнитного вектора с учетом их взаимной пространственной ориентации.

Как отмечалось, с учетом соотношений неразрывности компонентов лучевого вектора, можно получить выражения для амплитудного коэффициента отражения при совпадении плоскости поляризации и плоскости падения

,

где – амплитуда падающей волны, – амплитуда отраженной волны,  – угол падения,  – угол преломления.

Для ортогональной ориентации плоскости поляризации и плоскости падения коэффициент отражения может быть записан как

.

Амплитудные коэффициенты определяют мощностные коэффициенты отражения и . Из мощностных коэффициентов отражения исходя из соотношений энергетического баланса несложно получить мощностные коэффициенты пропускания и , а также амплитудные коэффициенты пропускания и .

Все основные соотношения для обоих случаев поляризации излучения, которые принято называть коэффициентами Френеля, можно свести в таблицу.

Соотношение	p-поляризация	s-поляризация
Амплитудный коэффициент отражения
Амплитудный коэффициент пропускания
Мощностной коэффициент отражения
Мощностной коэффициент пропускания

Особенности баланса энергии. Введем значение интенсивности неполяризованного света I. Для естественного (неполяризованного) света , а также . Вводится коэффициент общий отражения

.

С учетом того, что можно получить

.

Рассмотрим несколько частных случаев.

1. Пусть . Следовательно, и . Тогда для этого случая обозначим (угол Брюстрера). В этом случае при плоскости поляризации, совпадающей с плоскостью падения, отраженное излучение будет отсутствовать. Или, если на пластинку, ориентированную под углом Брюстера, падает естественно поляризованный свет, то отраженный луч будет полностью поляризован в ортогональной плоскости (s-поляризация).

Несложно определить значение угла Брюстера. Вспомним закон Снеллиуса . Тогда для угла Брюстрера имеем

.

Для воздуха , следовательно .

2. Пусть . Это случай так называемого зеркального падения излучения на пластину, тогда

, и , и .

3. Пусть (почти нормальное падение или его называют френелевским отражением), следовательно

.

Например, при (комбинация воздух-стекло) общий коэффициент френелевского отражения R = 0,04, т.е. чистая стеклянная поверхность обладает бликовой способностью по мощности в 4%. При наличие в оптической схеме, допустим, 10 оптических элементов, с двумя поверхностями в каждом, суммарный коэффициент пропускания схемы составит величину , т.е. френелевские потери на 20-ти свободных стеклянных поверхностях всего 10 оптических элементов составят более 50%!

При этом, чем выше относительный показатель преломления, тем больший уровень бликового отражения достигается. Например, для ZnSe, который является весьма распространенным материалом в ИК-технике, показатель преломления составляет величину n ~ 2,5, следовательно, нормальное френелевское отражение составит для него уже порядка 18%.

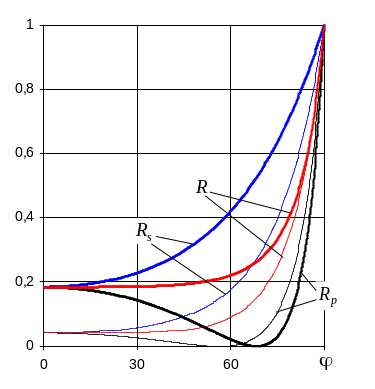
После того, как рассмотрены практически все характерные особенности процесса отражения от диэлектрической поверхности можно показать на примере границы раздела воздух-стекло с – тонкие линии и, для сравнения – границы раздела воздух-ZnSe с – толстые линии графики зависимостей коэффициентов отражения от угла падения .

Для стекла при все кривые начинаются с уровня 0,04 – френелевское отражение; при  все коэффициенты отражения приходят к 1 – случай зеркального отражения; как отмечалось, при  для выбранных условий – эффект Брюстера, причем глубина этого минимума такова, что в диапазоне углов  уровень коэффициента отражения не превышает значения 0,01 (1%) – другими словами «яма» минимального значения отражения для излучения с p-поляризацией достаточно пологая.

Для ZnSe ситуация аналогичная, с той лишь разницей, что , френелевский коэффициент отражения при составляет значение 0,184, а коридор 1%-го непревышения коэффициента отражения вокруг угла Брюстера сократился до интервала 62,8…69,7.

Еще более тонкие проявления френелевского отражения можно выявить в процессе анализа баланса фаз отраженного излучения. Однозначно это делается с помощью амплитудных коэффициентов отражения. Если амплитудный коэффициент меняет знак – это означает, что фаза излучения в процессе отражения меняет свое значение на . Эти скачки происходят в процессе падения излучения при переходе угла Брюстера.

Именно на этом изменении фазы можно решить две принципиальные задачи, связанные с френелевским отражением. Первая направлена на существенное снижение уровня бликовых отражений – просветление оптики, а вторая направлена на создание так называемых интерференционных зеркал. Обе задачи решаются одним и тем же методом – нанесением специальных покрытий на оптический элемент.

При подборе показателя преломления тонкого однослойного покрытия толщиной таким образом, чтобы отраженные пучки от двух слоев имели бы не только одинаковую интенсивность, но и разность фаз в . В результате этого произойдет взаимное интерференционное гашение отраженных волн, т.е. бликовое излучение будет в идеале устранено, как это показано на рисунке ниже. Именно устранение бликового излучения и называется просветлением оптических элементов. В реальности противобликовое интерференционное покрытие позволяет понизить коэффициент отражения как минимум на порядок.

В другом случае можно нанести на поверхность подложки много специальным образом организованных слоев так, чтобы отраженная волна от каждого последующего слоя была бы синфазна предыдущим. В результате получится эффект интерференционного суммирования волн от всех слоев, т.е. многослойное покрытие будет работать как зеркальная поверхность, настроенная на конкретную длину волн излучения. Чем больше слоев будет нанесено, тем меньшая доля излучения будет проникать вглубь подложки, т.е. тем большая часть излучения будет отражаться от многослойной структуры. В настоящее время известны интерференционные зеркала, содержащие несколько десятков слоев, обеспечивая тем самым эквивалентный коэффициент отражения падающей волны ~ 0,998.

1 В переводе эйконал означает изображение. Это сугубо историческое название.