2.1 Критерій Найквіста-Михайлова

Критерій Найквіста-Михайлова дозволяє робити висновки про стійкість замкнутої системи регулювання по амплітудно-фазовій частотній характеристики розімкнутої системи що дає можливість використовувати для оцінки стійкості результати експериментальних дослідів.

Амплітудно-фазова характеристика розімкнутої системи знаходиться з її операторної функції шляхом заміни оператора Р на jω. На комплексній площині будується амплітудно-фазова характеристика розімкненої системи шляхом зміни частоти ω від 0 до ∞. По виду цієї характеристики судять про стійкість системи в замкнутому стані.

Мал. 2.10.1 Амплітудно-фазові характеристики розімкнених систем 1 — стійка; 2 — нейтральна; 3 — нестійка

Критерій стійкості Михайлова

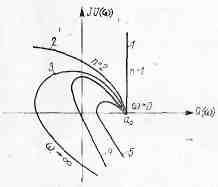
Критерій стійкості Міхайлова. Критерій стійкості Міхайлова — це частотний критерій, заснований па побудуй нді по характеристичному рівнянню системи так называвмій характеристичної кривої, або годографа, по вигляду кото рого судять про стійкість АСР.

Відмітивши в цьому рівнянні змін ную величиною jω, отримаємо:

це рівняння при зміні частоти з від 0 до +оо дозво­ляет побудувати на комплекс­ной плоскості годограф, по вигляду якого можна судити про стійкість системи.

Мал. 2.10.2 Годографи замкнутих си­стем регулювання

Критерій Михайлова фор­мується наступним обра­зом: система стійка, якщо годограф Михайлова при зміні частоти з від 0 до + оо, починаючись на додатній частині дійсна піввісь, огинає проти часо­вої стрілки початок коорди­нат, ніде не перетворюючись в нуль, проходячи послідовно таку кількість квадрантів комплексної плоскості, який ступінь характеристичного рівняння.

Мал. 2.10.2 годограф 1, 2, 3 характеризує стійку, а го­дограф 5 — нестійку, 4 — «граничну» системи.

Аналіз стійкості проводиться таким чином:

у характеристичному рівнянні замкнутої системи за­міняють Р на jω;

члени jω підносять до відповідних ступенів, після чого групують дійсну Q(ω) і уявну JU(ω) частини много­члена, які виписують окремо один від одного;

задаючись окремими значеннями з від 0 до + ∞ визначають величини Q(ω) і JU(ω) і будують криву по крапках, отриманих при певних значеннях з, відповідних точкам перетину годографа з осями координат. Щоб знайти точки перетину годографа з віссю дійсних значень, потрібно прирівняти нулю уявну частину годографа і з отриман­ного рівняння знайти значення частот, які потім підставити в вираз речовіоїчастини годографа. Отримані значення є абсцисами точок перетину годографа з віссю речових значень. Аналогічно, прирівнюючи нулю дійсну частину годографа, визначають ординати крапок, в яких годограф перетинає уявну вісь. По знайдених крапках будується годограф системи і проводиться оцінка її на стійкість.

2.1 Критерій стійкості Найквіста-Михайлова формулюється наступним чином: Замкнена система стійка, якщо амплітудно-фазова характеристика розімкнутої системи не охоплює на комплексній площині точку з координатами Q= -1, JU = 0. На рисунку 1 зображені амплітудно-фазові характеристики розімкнених систем які в замкненому стані стійкі (1), нестійкі (3) чи знаходяться на границі стійкості (2). На стійкість системи значно впливає запізнення.

Запізнення, яке має місце в реальних об’єктах ускладнює роботу АСР, погіршує якість процесу. Пояснюється це тим, що воздія регулятора на вхід об’єкта залежить від значення регулюємої величини на виході об’єкту в даний момент. Однак за час, обумовлений запізненням, стан об’єкта може змінитись, і воздія регулятора, який ще не прийняв цю зміну може бути напрямлена в сторону підсилення збурень на вході об’єкта, а не в сторону їх усунення. Наявність запізнення в об’єкті збільшує відхилення регулюємої величини від заданого значення, подовжує перехідний процес може призвести до нестійкого стану.

Послаблення нешкідливого впливу досягаються використанням в схемах проміжних параметрів регулювання, також приміненням регуляторів з передуванням і схем зв’язаного регулювання.