
ВВЕДЕНИЕ.
Элементы векторной алгебры.
Все физические величины делятся с математической точки зрения на скалярные и векторные.
Скалярные величины (скаляры) характеризуются только численными значениями и могут быть положительными или отрицательными.
Примеры: время t, масса m, электрический заряд q и др.
Скаляр может быть изображен геометрически в виде точки на числовой оси.
Векторные
величины
(вектора) характеризуются численным
значением (модуль вектора) и направлением.(
скорость
![]() ,
ускорение
,
ускорение
![]() ,
сила
,
сила
![]() и др).
и др).
Геометрически вектор изображается как направленный отрезок прямой.
В тексте вектор пишется буквой со стрелкой или жирным шрифтом.
Операции с векторами
1
Сложение векторов
![]()
а) правило параллелограмма:
- совмещаем
начала векторов a
и b
в одной точке;
совмещаем
начала векторов a
и b
в одной точке;
достраиваем получившуюся фигуру до параллелограмма,
д иагональ
параллелограмма выходящая из общей
вершины
иагональ
параллелограмма выходящая из общей
вершины
![]() есть
вектор суммы
есть
вектор суммы
![]() и
и
![]() .
.
б) правило треугольника (может быть использовано для n-векторов):
к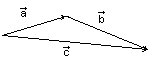 концу
концу
![]() присоединяется начало
,
присоединяется начало
,
вектор , начало которого совпадает с началом , а конец с концом , является суммой векторов и .
Численное значение вектора суммы ищем по теореме косинусов
![]() ,
где
,
где
![]() угол между векторами
и
.
угол между векторами
и
.
2. Вычитание векторов можно рассматривать как действие, обратное сложению
![]()
и пользоваться названными выше правилами:
-совмещаем начала векторов и в одной точке,
-1-
вектор
разности
![]() соединяет концы
и
,
и направлен в сторону уменьшаемого
вектора.
соединяет концы
и
,
и направлен в сторону уменьшаемого
вектора.
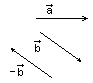

Численное значение вектора разности
![]() ,
где
,
где
![]()
Говоря
о разности векторов, введем понятие
изменение вектора
![]()
![]()
Разложение вектора на составляющие.
В физическом трехмерном пространстве вектор можно разложить на составляющие по трем произвольно заданным направлениям, т.о. что сумма трех составляющих векторов есть исходный вектор
Пример. Разложим вектор по двум заданным направлениям АВ и СD. двухмерного пространства:

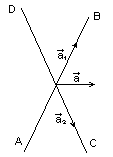
Ч
 ерез
начало и конец
проведем прямые линии, параллельные
АВ и CD
ерез
начало и конец
проведем прямые линии, параллельные
АВ и CDСтороны этого параллелограмма
 и
и
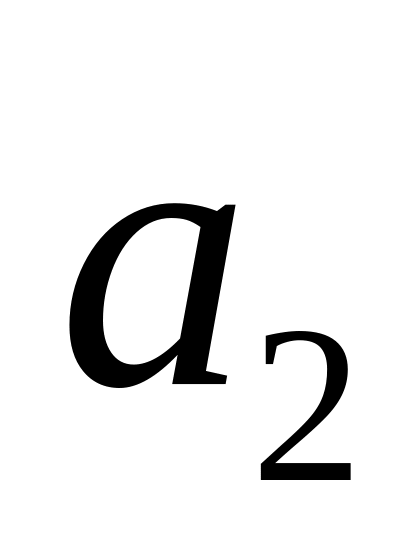 и есть составляющие вектора
.
и есть составляющие вектора
.
В случае трехмерного пространства вместо параллелограмма следует построить параллелепипед.
4. Проекции вектора на оси координат
Р
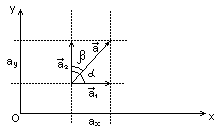 азложим
по составляющим по заданным направлениям
ОХ и ОY
(
,
– составляющие
)
азложим
по составляющим по заданным направлениям
ОХ и ОY
(
,
– составляющие
)
-2-
2.Из
точек начала и концов
и
опустим на оси координат перпендикуляры,
которые выделяют на них отрезки
![]() и
и
![]() – проекции вектора
.
– проекции вектора
.
Численное значение проекции вектора на оси координат определяется по формулам:
![]() ,
,
где
– угол между
и положительным направлением OX,
а
![]() – угол между
и положительным
направлением OY.
Проекция вектора - число. Оно может быть
положительным, если угол
острый
и отрицательным, если угол
тупой.
– угол между
и положительным
направлением OY.
Проекция вектора - число. Оно может быть
положительным, если угол
острый
и отрицательным, если угол
тупой.
5.Умножение
вектора на скаляр (в результате получаем
вектор),
![]() ,если
,если
![]() положительное число, то направление
положительное число, то направление
![]() ,
если
отрицательно, то направление
меняется на противоположное
,
если
отрицательно, то направление
меняется на противоположное
![]() .
.
6.Скалярное умножение векторов (в результате получаем скаляр). Обозначение:
![]()
Скалярное произведение векторов равно произведению их модулей на косинус угла между ними.
![]() ,где
– угол между векторами
и
.
,где
– угол между векторами
и
.
7.Векторное умножение векторов (в результате получаем вектор). Обозначение:
![]()
а)
величина
![]() ,
где
– угол между
и
,
отсчитываемый от
к
против часовой стрелки;
,
где
– угол между
и
,
отсчитываемый от
к
против часовой стрелки;
б) вектор перпендикулярен к перемножаемым векторам, т.е. к плоскости, в которой эти вектора расположены. Направление ищем по правилу буравчика: рукоятку буравчика вращают от первого сомножителя ко второму по наикратчайшему пути, тогда движение острия буравчика, установленного в точке общего начала векторов, дает направление вектора векторного произведения
-3-
КИНЕМАТИЧЕСКИЕ ПАРАМЕТРЫ.
Кинематика – это раздел механики, изучающий параметры движения, связь между ними и основные законы движения без рассмотрения причин, их вызывающих.
Материальная точка – любое реально существующее тело, размерами которого в условиях данной задачи можно пренебречь.
Траектория – линия, которую описывает материальная точка в пространстве с течением времени. Положение материальной точки в пространстве может быть определено радиус-вектором
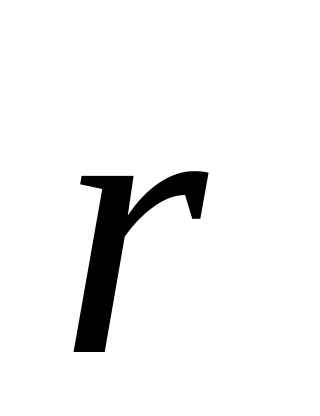 или координатами в выбранной системе
отсчета.
или координатами в выбранной системе
отсчета.
3 . Система отсчета – совокупность системы координат, тела отсчета и начала отсчета времени.
Радиус-вектор соединяет тело отсчета и движущуюся материальную точку – .
5. Вектор
перемещения
соединяет
начальное и конечное положения точки
–
![]() .
Изменение радиус-вектора точки равно
вектору перемещения за то же время:
.
Изменение радиус-вектора точки равно
вектору перемещения за то же время:
![]() .
Радиус-вектор в прямоугольной системе
координат
.
Радиус-вектор в прямоугольной системе
координат
![]() где
где
![]() – проекции радиус-вектора на координатные
оси, x,y-координаты
точки.
– проекции радиус-вектора на координатные
оси, x,y-координаты
точки.
Путь – расстояние, проходимое точкой вдоль траектории. Длина вектора перемещения равна пройденному пути только при прямолинейном однонаправленном движении.
Скорость характеризует быстроту изменения радиуса вектора точки:
![]() – средняя
скорость перемещения (вектор);
– средняя
скорость перемещения (вектор);
![]() – средняя
скорость движения (скаляр).
– средняя
скорость движения (скаляр).
![]() – мгновенная
(истинная) скорость, равна производной
от радиус-вектора по времени, направлена
по касательной к траектории.
– мгновенная
(истинная) скорость, равна производной
от радиус-вектора по времени, направлена
по касательной к траектории.
![]() ,
,
где
![]() – характеризует быстроту изменения
радиус-вектора по модулю, направлена
вдоль радиус-вектора (тангенциальная
составляющая);
– характеризует быстроту изменения
радиус-вектора по модулю, направлена
вдоль радиус-вектора (тангенциальная
составляющая);
-4-
![]() – характеризует
быстроту изменения радиус-вектора по
направлению, направлена перпендикулярно
радиус-вектору (нормальная составляющая).
– характеризует
быстроту изменения радиус-вектора по
направлению, направлена перпендикулярно
радиус-вектору (нормальная составляющая).
Ускорение
характеризует быстроту изменения
вектора скорости:
,
![]()
![]() – характеризует
быстроту изменения вектора скорости
по модулю;
– характеризует
быстроту изменения вектора скорости
по модулю;
![]() – характеризует
быстроту изменения вектора скорости
только по направлению;
– характеризует
быстроту изменения вектора скорости
только по направлению;
![]() –
равна
производной от модуля скорости;
–
равна
производной от модуля скорости;
![]() ,
где
R
радиус кривизны траектории.
,
где
R
радиус кривизны траектории.
