1.4.3. Теорема разложения (Хэвисайда)
Эта теорема позволяет сравнительно просто получить обратное преобразование Лапласа.
Пусть
где М(р)
и
N(p)
- полиномы степени М
и N
соответственно.
Тогда, если M < N и
N(p) не содержит нулевых корней
то
(1.4.31)
где pk – корни полинома N(p), N-число корней полинома N(p).
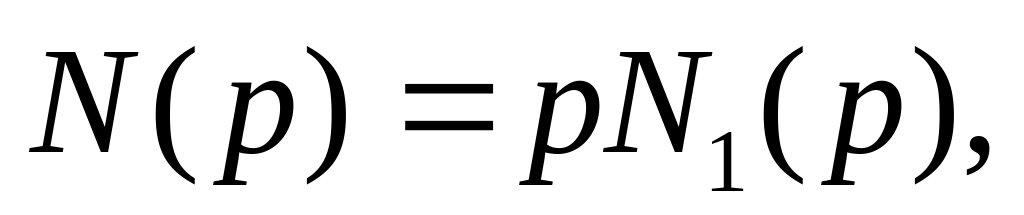N1(p)
– полином степени
N1
и не содержит нулевых корней и
М < N1.
Тогда
(1.4.32)
где pk – корни полинома N1(p), N1-число корней полинома N1(p).
*) штрих при N и N1 обозначает производную по р.
Если М > N, то необходимо поделить М(р) на N(p), выделить целую и дробную часть и, используя свойство линейности и применяя для дробной части теорему разложения, найти оригинал.
Если N(р) содержит к нулевых корней, причем М<N1, то S(p) представляется в виде суммы простых дробей и при использовании свойства линейности находится оригинал. Рассмотрим на примере.
Модулированные сигналы
Модулированным сигналом называется высокочастотное колебание, один из параметров которого изменяется по закону передаваемого сообщения.
Модулированные сигналы подразделяются на непрерывные (аналоговые) и сигналы с импульсной модуляцией.
Непрерывные сигналы подразделяются на амплитудномодулированные (амплитда высокочастотного колебания изменяется по закону передаваемого сообщения) и сигналы с угловой модуляцией.
Последние подразделяются на:
Фазомодулированные сигналы (мнгновенная фаза высокочастотного колебания изменяется по закону передаваемого сообщения);
частотномодулированные сигналы (мнгновенная частота высокочастотного колебания изменяется по закону передаваемого сообщения).
Сигналы с импульсной модуляцией подразделяются на сигналы с:
амплитудно - импульсной модуляцией (амплитуда импульсов изменяется по закону передаваемого сообщения) - АИМ - сигналы;
широтно - импульсной модуляцией (длительность импульсов изменяется по закону передаваемого сообщения) - ШИМ - сигналы;
частотно - импульсной модуляцией (частота импульсов изменяется по закону передаваемого сообщения) - ЧИМ - сигналы;
фазо - импульсной модуляцией (начальная фаза импульсов изменяется по закону передаваемого сообщения) - ФИМ - сигналы;
время - импульсной модуляцией (интервал между импульсами изменяется по закону передаваемого сообщения) - ВИМ – сигналы и др.
Импульсные сигналы подразделяются на простые и сложные.
Для простых сигналов произведение ширины спектра ∆f = ∆ω/2π на длительность сигнала ∆t близко к единице, т.е.
∆f × ∆t ≈ 1. (1.5.1)
Для сложных сигналов
∆f × ∆t >> 1. (1.5.2)
К наиболее часто используемым сложным сигналам относятся сигналы с внутри-импульсной частотной линейной (ЛЧМ) и нелинейной (НЧМ) модуляцией и фазоманипулированные сигналы, состоящие из конечного числа отрезков гармонических колебаний одинаковой длительности, начальная фаза которых может принимать одно из конечного числа дискретных значений (например, 0 или π).