3. Решение задачи нелинейного программирования при ограничениях-равенствах

В данном разделе рассматривается оптимизационная ЗНЛП вида

(3.1)

; , (3.2)

которая в более компактной векторной форме записи имеет вид

(3.3)

Здесь: – целевая функция; – ее векторный аргумент (вектор неизвестных); – вектор-функция ограничений; – заданный вектор правой части ограничений.

3.1. Метод множителей Лагранжа

3.1.1. Назначение и обоснование метода

Метод множителей Лагранжа предназначен для решения ЗНЛП типа (3.1)-(3.2), которая в развернутой форме записи имеет вид

(3.4)

(3.5)

Для безусловного экстремума, когда ограничений нет, и экстремум ищется на всем пространстве, необходимым условием существования экстремума является условие . В случае одного условия область ограничений состоит из поверхности ; градиент целевой функции в точке экстремума должен быть ортогонален к этой поверхности. В противном случае в касательной плоскости существует направление, вдоль которого производная от функции отлична от нуля (тогда и производная вдоль кривой на поверхности, касающейся этого направления, отлична от нуля). Поэтому, вследствие ортогональности градиента в точке экстремума к поверхности , при некотором должно выполняться

,

иначе говоря, при некотором

.

В случае нескольких ограничений в виде системы уравнений, когда допустимое множество представляет собой поверхность

,

градиент должен лежать в нормальной плоскости к поверхности, то есть в плоскости, «натянутой» на векторы

.

Следовательно, при некоторых Имеем,

,

то есть

,

что является необходимым условием существования экстремума.

Это условие и ложится в основу метода множителей Лагранжа.

3.1.2. Схема реализации метода множителей Лагранжа

Метод реализуется выполнением следующих шагов.

Шаг 1. Вводится вектор , компоненты которого называются множителями Лагранжа.

Шаг 2. Определяется функция Лагранжа в виде суммы целевой функции и скалярного произведения вектора множителей Лагранжа на вектор разности между правой и левой частями ограничений:

, (3.6)

которая в развернутой форме записи имеет вид

. (3.7)

Здесь вектор инструментальных переменных функции Лагранжа.

Шаг 3. Производится отыскание стационарных точек функции Лагранжа. Для этого в соответствии с необходимыми условиями существования безусловного экстремума решается система уравнений

(3.8)

Здесь 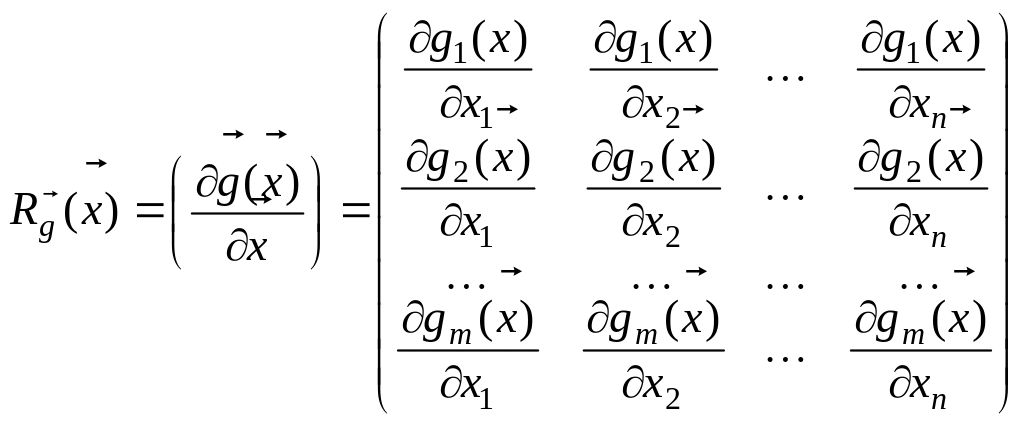– матрица Якоби вектор-функции .

Систему уравнений (3.8) нетрудно представить в развернутом виде:

(3.9)

Шаг 4. Каждая из найденных стационарных точек проверяется на экстремум. Для этого в рассмотрение вводится так называемая окаймленная матрица Гессе , определяемая следующим образом:

,

где – нулевая матрица; матрица Якоби вектор-функции ограничений; матрица Гессе функции Лагранжа (составлена из производных второго порядка функции Лагранжа по инструментальным переменным).

Достаточными условиями, определяющими тип условного экстремума функции при ограничениях в стационарной точке, являются следующие:

1) точка является точкой максимума, если все главные миноры окаймленной матрицы Гессе начиная с главного минора порядка , образуют знакопеременный ряд, знак первого члена которого определяет множитель .

2) точка является точкой минимума, если знаки всех главных миноров окаймленной матрицы Гессе начиная с главного минора порядка , определяются множителем .