18

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

Кафедра теоретической и геотехнической механики

Кинематика плоского механизма

Методические указания к выполнению самостоятельной

работы по курсу "Теоретическая механика" для студентов

специальности 170100  «Горные машины и оборудование»

Составитель Е. К. Соколова

Утверждены на заседании кафедры

Протокол № 11 от 18.02. 2008

Рекомендованы к печати

учебно-методической комиссией

специальности 170100

Протокол № 8 от 29.02. 2008

Электронная копия находится

в библиотеке главного корпуса

ГУ КузГТУ

Кемерово 2008

ВВЕДЕНИЕ

Изучаемые в кинематике законы движения материальных объектов, аналитические и графо-аналитические методы расчета кинематических характеристик отражают разнообразие движений в природе и технике.

Любая технологическая машина осуществляет рабочий процесс посредством выполнения закономерных механических движений, реализуемых соответствующими механизмами. Механизм есть система твердых тел, подвижно связанных путем соприкосновения и движущихся определенным образом относительно одного из них, принятого за неподвижное. Механизм выполняет функцию преобразования механического движения твердых тел.

Если звенья механизма движутся в параллельных плоскостях, механизм называют плоским. Примером плоского механизма могут служить кривошипно-кулисный и кривошипно-шатунный механизмы.

В теме «Кинематика точки» изучались векторный и координатный способы задания движения точки. Если выделить наиболее важные точки, определяющие движение всего механизма, то весь механизм можно представить в виде векторного контура, то есть задать движение векторным способом. От векторного способа задания движения можно переходить к координатному способу. Тогда для определения кинематических характеристик точек механизма можно использовать методы расчета, полученные в «Кинематике точки».

Аналитический расчет кинематики кривошипно-шатунного механизма

ЗАДАЧА.

В кривошипно-шатунном механизме (рис. 1) угол поворота кривошипа ОА изменяется по закону φ = φ(t).

Зная длину кривошипа ОА и шатуна АВ, найти:

уравнение движения и траекторию точки С₃ середины шатуна;

уравнение движения ползуна В;

выразить координа­ты точек А, С₁, С₃ в зависимости от угла поворота кривошипа.

Определить проекции скорости и скорость, проекции ускорения и ускорение точек А, В, С₁, С₃ на оси неподвижной декартовой системы координат в момент времени, когда φ = φ1.

Исходные данные для каждого варианта представлены в таблице 1.

(При расчетах можно воспользоваться программой Mathcad).

Таблица 1

Вариант	Закон движения кривошипа	ОА, м	АВ, м	ω0, рад/с	ε1, рад/с	а	b
1.1 – 1.35	φ = ω0t + ε1t2/2	0,3	0,7	1	1	–	–
2.1 – 2.35		0,4	0,6	2	1	–	–
3.1 – 3.35		0,5	0,9	3	2	–	–
4.1 – 4.35	φ = a sin bt	0,3	0,5	–	–	2π	1
5.1 – 5.35		0,5	0,8	–	–	2π	2
6.1 – 6.35		0,5	0,9	–	–	2π	π/3
7.1 – 7.35	φ = a cos bt	0,4	1,0	–	–	2π	π/4
8.1 – 8.35		0,8	1,2	–	–	2π	2
9.1 – 9.35		0,3	0,6	–	–	2π	3

Примечание: вторая цифра в номере варианта соответствует тому значению угла поворота кривошипа ОА, для которого производятся расчеты (№ 1 – φ₁=10⁰, № 2 – φ₁=20⁰, … , № 35 – φ₁=350⁰).

ПРИМЕР РАСЧЕТА

В кривошипно-шатунном механизме (рис. 1) кривошип ОА = r₁ вращается по закону φ = φ(t). Длина шатуна АВ = r₃. Определить скорость и ускорение точек А, В, С₁, С₃ в моменты времени, соответ­ствующие положению механизма при угле поворота кривошипа φ = φ ₁.

Р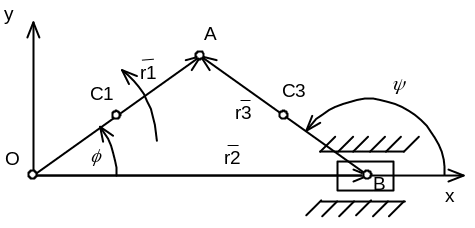 ис. 1

Для определения кинематических характеристик любой точки кривошипно-шатунного механизма представим его в виде векторного контура

.

Проецируем обе части векторного уравнения на оси Ох и Оу неподвижной декартовой системы координат

Из полученной системы уравнений определим неизвестные пере­менные величины

;

;

.

Обозначим .

Тогда закон движения ползуна В можно записать в виде

Зная зависимость от времени угла ψ = ψ(t), можем определить координаты любой точки шатуна АВ как функции времени.

Законы движения точек механизма

Координаты точек А, В, C₁, соответственно, равны

Определим координаты центра шатуна АВ – точки С₃

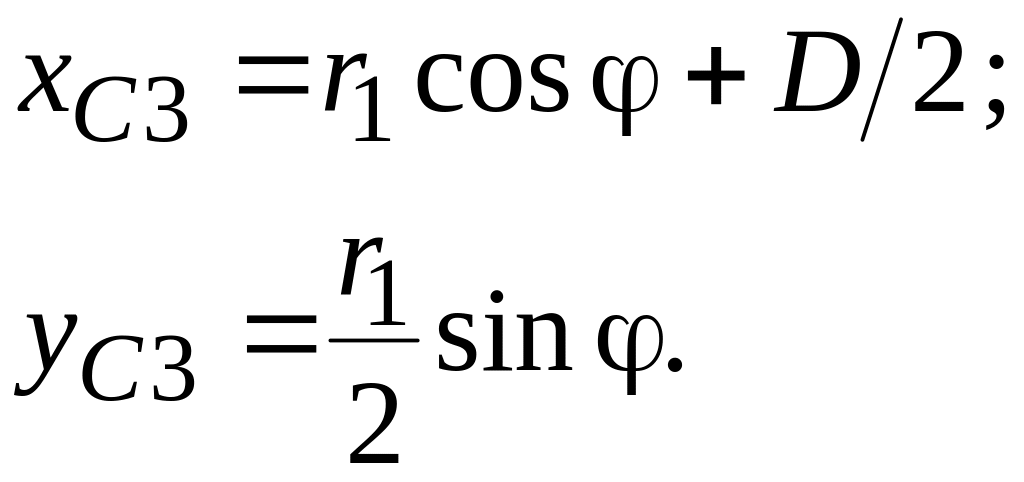
Зная координаты точек А, В и С₃ , можно построить изображение механизма в любой момент времени и определить траекторию точки С₃.