9.5. Примеры решения типовых задач

Пример 9.1. Привести к каноническому виду уравнение второго порядка .

Решение. В этом уравнении а₁₁ = 8, а₁₂ = 2, а₂₂ = 5, а₁₃ = 8, а₂₃ = 2, а₃₃ = 28. Подставив значения коэффициентов в инвариант , убедимся, что

,

то есть мы имеем дело с эллипсом.

Подставив значения коэффициентов в уравнения (9.20) и решив систему

найдем координаты центра симметрии эллипса: .

Подставив эти числа в уравнения (9.21), найдем новое значение свободного члена

.

После переноса начала координат в центр симметрии эллипса его уравнение приобретает следующий вид:

. (9.26)

Перекрестный член в этом уравнении уничтожается за счет поворота осей координат. Тангенс угла поворота определяем из уравнения (9.23):

Коэффициенты и найдем, используя инварианты:

(Если , то .)

В итоге уравнение эллипса примет следующий вид:

или

. (9.27)

Рис. 9.5

Пример 9.2. Привести к каноническому виду уравнение второго порядка

. (9.28)

Решение. Значения коэффициентов уравнения:

Подставив эти значения в инвариант , убедимся, что

,

то есть мы имеем дело с параболой.

Преобразования начнем с поворота осей координат. Тангенс угла поворота определяем из уравнения (9.23):

,

(последние формулы справедливы для ).

Подставим в уравнение (9.28) значения х и у:

,

и получим

Перегруппируем члены уравнения:

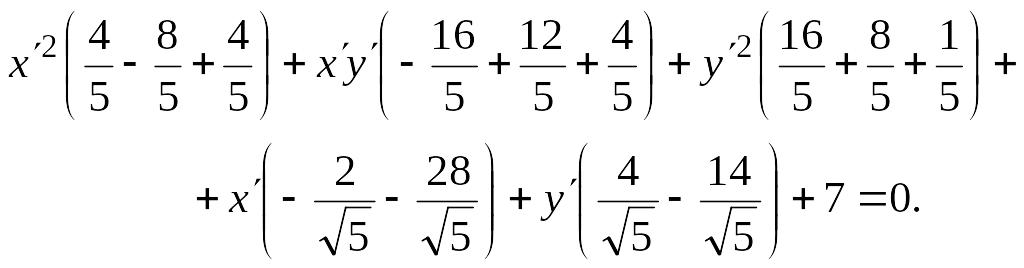
После упрощений получим:

.

В итоге получено уравнение параболы, ось симметрии которой повернута на угол , а вершина находится в точке .

Вопросы для повторения

1. Определения эллипса, гиперболы и параболы.

2. Канонические уравнения эллипса, гиперболы и параболы.

3. Общее определение кривых 2-го порядка с использованием понятий директрисы и эксцентриситета кривой.

4. Полярные уравнения кривых 2-го порядка.

5. Упрощение общего уравнения кривой 2-го порядка при переносе начала декартовой системы координат в центр симметрии кривой.

6. Упрощение общего уравнения кривой 2-го порядка при повороте осей координат.

7. Инварианты преобразований координат и их использование при приведении общего уравнения кривых 2-го порядка к каноническому виду.

Рекомендуемая литература

1. Ильин В. А., Позняк Э. Г Аналитическая геометрия. – М.: Физматлит, 2001, 2002.

2. Клетеник Д. В. Сборник задач по аналитической геометрии. – СПб: Мифрил, 2001.

3. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. – Феникс, 1997.

Содержание

Предисловие 3

1. Системы линейных уравнений. Матрицы и определители 4

2. Системы координат 21

3. Векторная алгебра 26

4. Произведения векторов 35

5. Прямая линия на плоскости 42

6. Плоскость в трехмерном пространстве 51

7. Прямая линия в трехмерном пространстве 60

8. Примеры решения основных задач на прямую

и плоскость 65

9. Кривые второго порядка 69

Рекомендуемая литература 79

Редактор Е. Н. Кочубей

Подписано в печать 24.02.2009 . Формат 60х84 1/16

Печ. л. 5,0. Уч.-изд. л. 5,0. Тираж 100 экз.

Изд. № 001-1. Заказ №

Московский инженерно-физический институт (государственный университет).

Типография МИФИ. 115409, Москва, Каширское ш.,31

81