3.3. Вектор в декартовой прямоугольной системе координат

Определим проекцию вектора на ось . Проекции точек М₁ и М₂ на ось Ох – точки М_1х и М_2х. Это точки пересечения с осью Ох плоскостей и , проведенных через точки М₁ и М₂ перпендикулярно оси Ох (рис. 3.3). Проекцией вектора на ось Ох называется величина отрезка М_1хМ_2х:

. (3.17)

Здесь х₁ и х₂ – координаты точек начала и конца отрезка М_1хМ_2х.

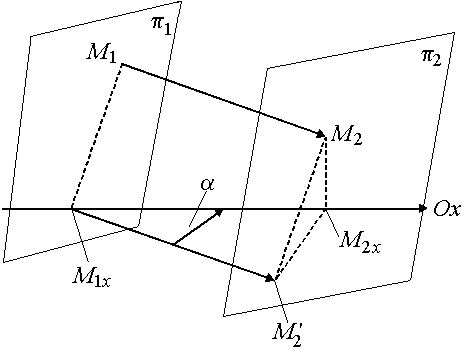Рис. 3.3

С другой стороны, если перенести вектор М₁М₂ (оставляя его параллельным исходному положению) до совмещения точек и то проекцию вектора можно представить так:

. (3.18)

Проекция вектора на ось Ох

. (3.19)

Аналогично представляются проекции вектора на оси Оу и Оz:

(3.20)

. (3.21)

В трехмерном пространстве принято использовать базис из трех взаимно ортогональных векторов единичной длины и , которые являются ортами осей декартовой прямо-угольной системы координат. Такой базис называется ортонормированным.

Вектор может быть разложен по базису , то есть

. (3.22)

Рис. 3.4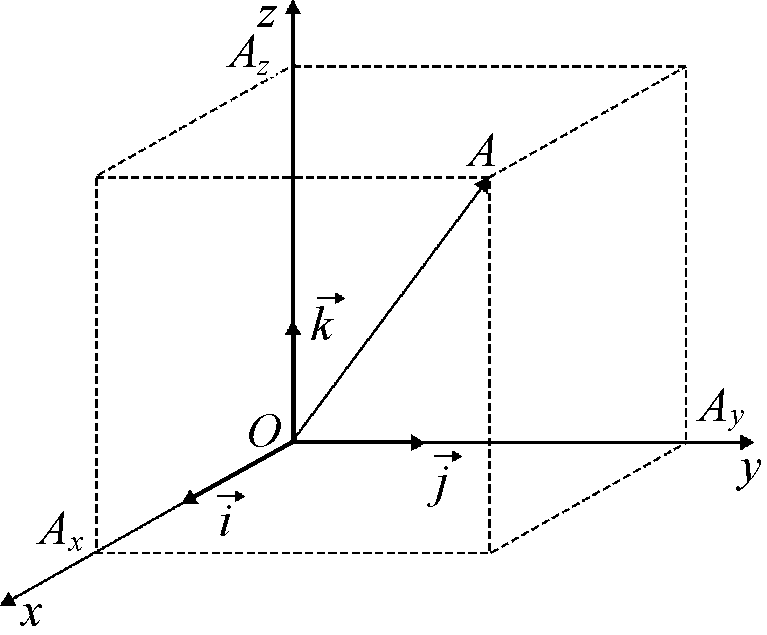

Коэффициенты разложения Х, Y, Z, опрелены однозначно, так как равны проекциям вектора на оси координат. Если совместить начало вектора с началом координат (рис. 3.4), то вектор . Проекции вектора на оси координат равны величинам отрезков .

В соответствии с правилами сложения векторов

. (3.23)

С учетом соотношений (3.19), (3.20) и (3.21) можно записать:

, (3.24)

где – орт вектора . Разложение орта по базису имеет вид

. (3.25)

В соответствии с теоремой Пифагора для трехмерного случая

, (3.26)

а также

(3.27)

Принято называть и направляющими косинусами вектора , и – углы между вектором и осями и .

(3.28)

Задачи для самостоятельного решения [2]: № 752, 757, 763, 781, 784, 785.

Вопросы для повторения

1. Понятие вектора. Линейные операции над векторами. Системы аксиом для операций сложения векторов и умножения вектора на число.

2. Линейная зависимость векторов – определение. Теорема о линейной зависимости векторов и её следствия.

3. Базис трехмерного пространства – определение. Разложение вектора по базису и координаты вектора относительно базиса. Теорема о единственности разложения вектора по базису. Теорема о преобразованиях координат вектора при сложении векторов и умножении вектора на число.

4. Ортонормированный базис в трехмерном пространстве. Орты декартовых осей координат. Правая и левая системы ортов и осей координат.

5. Проекции вектора на оси декартовой системы координат. Направляющие косинусы вектора. Орт вектора и его представление через направляющие косинусы.

4. Произведения векторов

Определение 4.1. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

(4.1)

(скалярное произведение принято обозначать круглыми скобками).

Используя представление проекции вектора на другой вектор, можно записать

. (4.2)

Теорема 4.1. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.

Доказательство. Если оба вектора ненулевые, то доказательство необходимости и достаточности утверждения теоремы следует из того факта, что необходимым и достаточным условием равенства нулю является условие , то есть

. (4.3)

Скалярное произведение имеет следующие свойства:

1) ;

2) , где − число;

3) ;

4) , если , , если .

Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, вынося за скобки числовые множители.

Теорема 4.2. Проекция вектора на вектор равна скалярному произведению вектора на орт вектор .

Доказательство. Из соотношения (4.2) следует, что

. (4.4)

Теорема 4.2. Если вектора и представлены в виде разложений по базису :

, (4.5)

то скалярное произведение этих векторов равно следующему выражению:

. (4.6)

Доказательство. Перемножив векторные многочлены (4.5), получим:

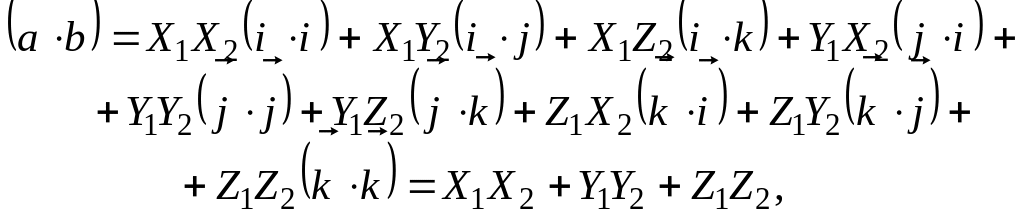(4.7)

поскольку

(4.8)

а остальные скалярные произведения ортов , ввиду их ортогональности, обращаются в нули.

Следствие 1.

(4.9)

Здесь орт вектора

(4.10)

Следствие 2.

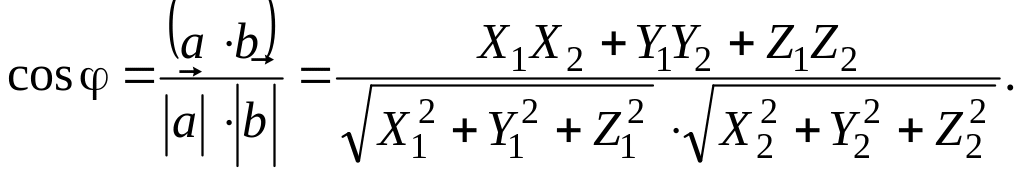(4.11)

Определение 4.2. Векторным произведением вектора на вектор называется вектор , обозначаемый символом (векторное произведение обозначают квадратным скобками) и удовлетворяющий трем требованиям:

1. вектор ортогонален к каждому из векторов и ,

2. длина вектора равна произведению модулей перемножаемых векторов на синус угла между ними:

(4.12)

3. упорядоченная тройка векторов 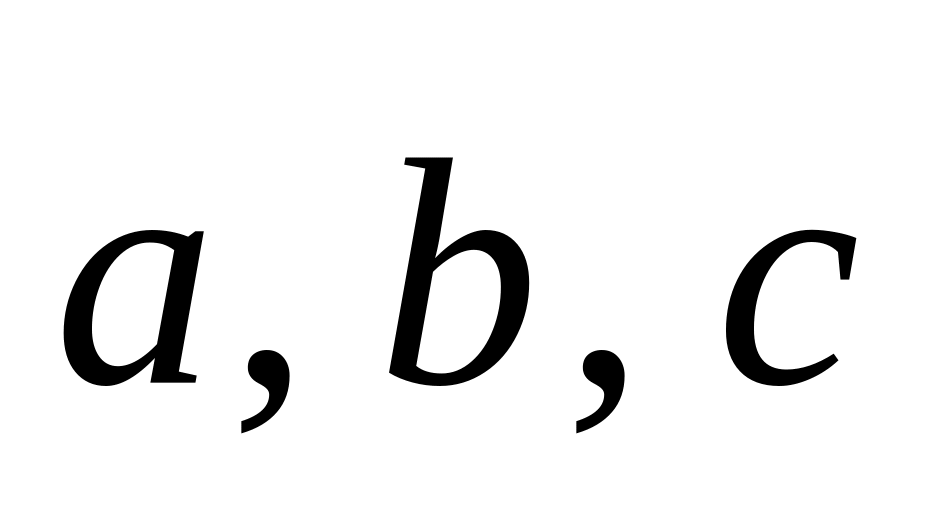является правой.

Определение 4.3. Упорядоченная тройка некомпланарных векторов является правой, если, после приведения векторов к общему началу, вектор располагается так, что из его конца кратчайший поворот от к виден происходящим в направлении против часовой стрелки. (В противном случае тройка векторов считается левой.)

Это утверждение справедливо для тройки векторов и для системы декартовых координат в пространстве.

Векторное произведение имеет следующие алгебраические свойства:

1) (антиперестановочность);

2) ,

3) ,

4) .

Теорема 4.3. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Доказательство. Если и , то доказательство необходимости и достаточности утверждения теоремы следует из (4.12) и того факта, что условие при также является необходимым и достаточным.

Теорема 4.4. Модуль векторного произведения равняется площади S параллелограмма, построенного на приведенных к общему началу векторах и .

Доказательство. Поскольку площадь параллелограмма равна произведению длин его смежных сторон на синус угла между ними. Доказательство теоремы следует из формулы (4.12).

Теорема 4.5. Если векторы представлены разложениями по базису :

, (4.13)

то их векторное произведение имеет вид:

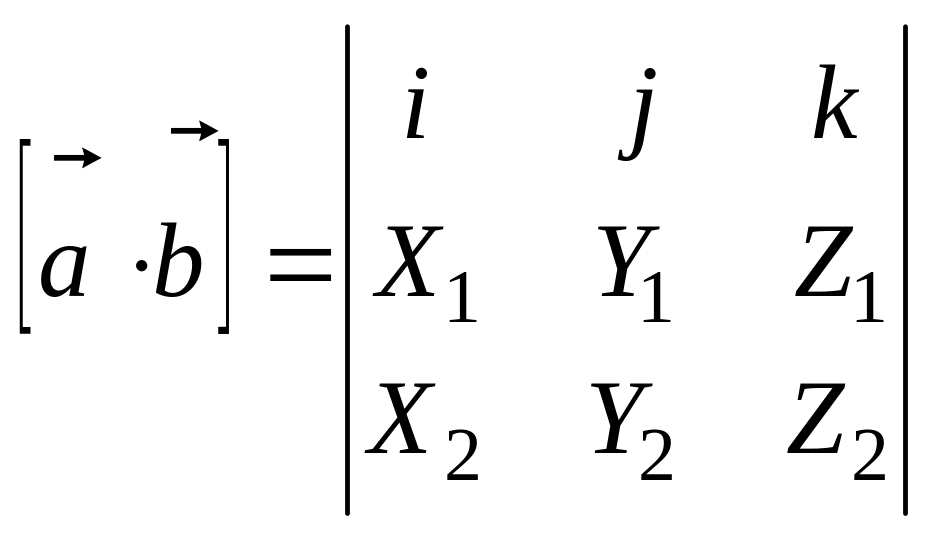. (4.14)

Доказательство. Перемножив векторные многочлены (4.13), получим, что

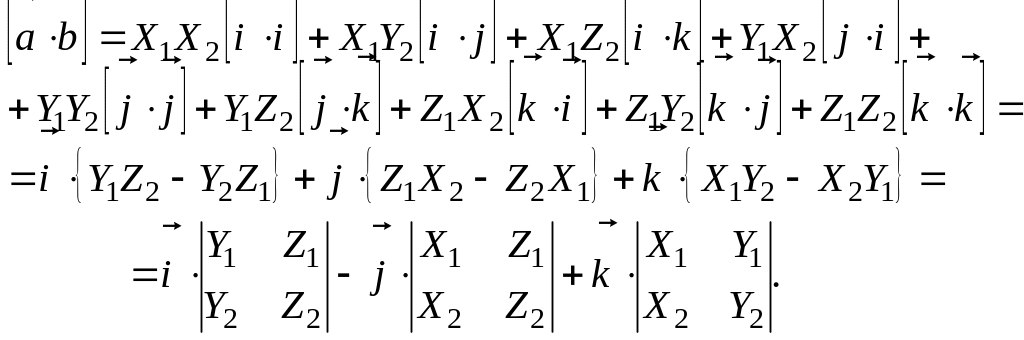(4.15)

Третья строка выражения (4.15) получена с учетом того, что

(4.16)

(Знак минус в этих произведениях получается вследствие нарушения порядка в тройке ортов .)

Очевидно, что выражение (4.15) есть разложение определителя (4.14) по элементам первой строки.

Теорема доказана.

Следствие. Если два вектора и коллинеарны, то координаты их пропорциональны, т.е.

(4.17)

Доказательство. Поскольку векторное произведение коллинеарных векторов равно нулю, из соотношения (4.15) следует, что

. (4.18)

Из первого равенства после деления на произведение получим пропорцию . Аналогичным образом из второго равенства получаем пропорцию . Следствие доказано.

В пропорции (4.17) возможно появление нулей в знаменателе. В соответствии с (4.18) это означает, что соответствующий числитель тоже равен нулю.

Для последующих выкладок нам удобно считать, что .

Следствие 1. Если −орт вектора , а − площадь параллелограмма, построенного на перемножаемых векторах, приведенных к общему началу, то

. (4.19)

Определение 4.4. Если векторное произведение умножить скалярно на вектор , то число ( ) называется смешанным произведением векторов и .

Теорема 4.6. Смешанное произведение ( ) равно объёму параллелепипеда, построенного на приведенных к общему началу векторах и , взятому со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка левая. Если же перемножаемые векторы компланарны, то их смешанное произведение ровно нулю (рис. 4.1).

Доказательство. Тривиальный случай коллинеарности векторов и исключим, так как векторное произведение коллинеарных векторов равно нулю. Тогда, используя выражение (4.19), можно произвести следующее преобразование

( ) = (4.20)

(Знак + берем в случае, если тройка векторов правая.)

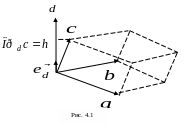
Если же вектора и компланарны, то вектор лежит в плоскости векторов и , следовательно, и . Теорема доказана.

Следствие 1. Справедливо равенство

(4.21)

Объём параллелепипеда не зависит от того, какая пара векторов из тройки перемножается векторно. Знак произведения не изменяется, так как сохраняется порядок векторов и ориентация тройки векторов.

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Теорема 4.7. Если три вектора представлены разложениями по базису :

,

то их смешанное произведение равно следующему определителю:

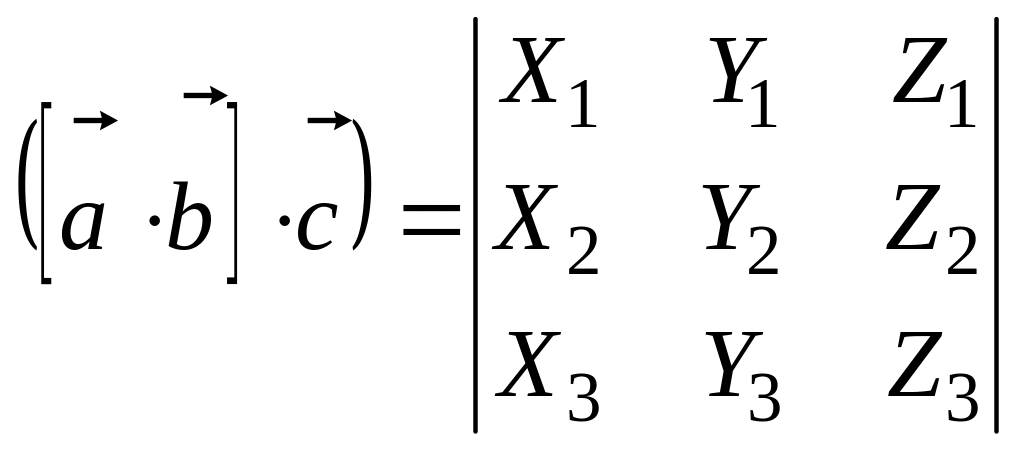. (4.22)

Доказательство. Из формулы (4.15) следует, что:

Умножив скалярно этот вектор на вектор , получим,

. (4.23)

Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки.

Теорема доказана.

Задачи для самостоятельного решения [2]: № 795, 800, 803, 812, 818, 820, 829, 834, 840, 847, 851, 858, 875, 877.