Алгоритм виконання лабораторного заняття

1. Уважно продумайте мету роботи,

2. Вивчити і охарактеризувати вимірювальні прилади, якими будете користуватися:

• визначте ціну поділки і розмір шкали,

• знайдіть похибку вимірювань даним приладом.

3. Зробіть необхідні малюнки і креслення та заповніть таблиці,

4. Визначте закономірність процесів, які ви спостерігали,

5. Запишіть показники приладів; врахуйте, що ні один вимірювальний прилад не дає точного значення вимірювальної величини.

6. Зробіть необхідні розрахунки, користуючись законами, описуючими дані явища.

7. Зробіть висновок, визначте головне в спостереженнях та розрахунках.

Правила поводження при виконанні лабораторного заняття

1. При виконанні лабораторних робіт дотримуйтесь техніки безпеки.

2. Дотримуватись правил техніки безпеки та безпеки життєдіяльності.

3. На заняття з'являтись вчасно без запізнень.

4. Слідкувати за зовнішнім виглядом, з'являтись на заняття у відповідній формі одягу;

5. Бути ввічливим, з повагою ставитись до викладачів, курсантів, технічного персоналу.

6. Адекватно реагувати на зауваження викладачів.

7. Дотримуватись нормативної лексики.

8. Дбайливо ставитись до майна лабораторії.

Лабораторне заняття № 21

Тема: Дослідження поляризованого світла та перевірка закону Малюса.

Мета роботи: дослідити закономірність поширення поляризованого світла та експериментально визначити залежність інтенсивності світла від кута між площинами поляризації двох поляризаторів.

Прилади та обладнання: оптична лава, збиральна лінза, освітлювач, два повзунки зі штативами та поляроїдами, фотоелемент, вольтметр.

Теоретичні відомості

Х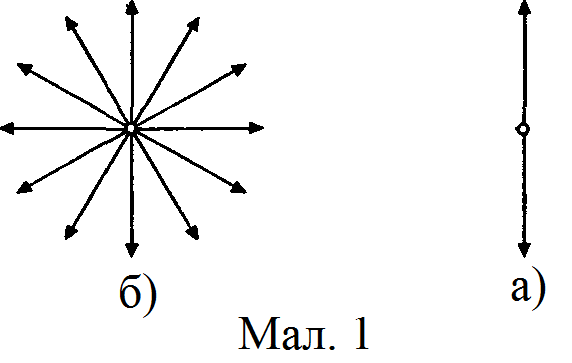 вилю, в якій напрямок коливань світлового вектора напруженості упорядкований називають поляризованою. Якщо коливання вектора відбуваються тільки в одній площині, що проходить вздовж променя, то хвиля називається поляризованою (мал. 1а). Площину, у якій коливається вектор , називають площиною поляризації. Світлові хвилі від звичайних джерел світла не виявляють асиметрії стосовно напрямку поширення. Таке світло називають природнім (мал.. 1б). У природньому світлі коливання вектора в будь-якій точці середовища відбуваються за різними напрямками. Природне світло можна розглядати як накладення (суму) двох некогерентних плоскополяризованих хвиль із взаємно ортогональними площинами поляризації. З природного світла можна одержати плоскополяризоване за допомогою приладів, називаних поляризаторами. Ці прилади пропускають коливання світлового вектора, паралельні площині поляризації Коливання ж, перпендикулярні до цієї площини, затримуються цілком або частково. Крім плоскополяризованого і природного світла існує частково поляризоване світло. Частково поляризоване світло, як і природне, можна розглядати як накладання двох некогерентних плоскополяризованих хвиль із взаємно перпендикулярними площинами поляризації, але різними за інтенсивністю. Його можна розглядати також як суму природної і плоскополяризованої складових.

З малюнка видно, що вертикальні коливання відповідають максимальній інтенсивності, горизонтальні – мінімальній.

Частково поляризоване світло характеризують ступенем поляризації Р, що визначають як

Тут I_пол – інтенсивність поляризованої складової, I₀ – повна інтенсивність частково поляризованого світло. Для плоскополяризованого світло (I_пол= I₀) ступінь поляризації Р=1, для природного світла (I_пол=0) Р=0.

Закон Малюса. У 1809 році французький інженер Э. Малюс відкрив закон, названий його ім'ям. У дослідах Малюса світло послідовно пропускалося через дві однакові пластинки з турмаліну (прозора кристалічна речовина зеленуватого кольору). Пластинки могли повертатися одна відносно іншої на кут φ. Якщо падаюче світло має інтенсивність I₀, то інтенсивність світла, яке пройшло через пластинку I виявилася прямо пропорційної cos² φ:

.

Отримане співвідношення називається законом Малюса.

Розглянемо проходження природного світла послідовно через два ідеальних поляроїда П1 і П2. Напрямки за якими пропускається світло, повернуті на деякий кут φ. Перший поляроїд відіграє роль поляризатора. Він перетворює природне світло в лінійно поляризоване. Нехай інтенсивність природного світла I₀. Тоді інтенсивність світла, що пройшло через поляризатор буде . Другий поляроїд служить для аналізу падаючого на нього світла.

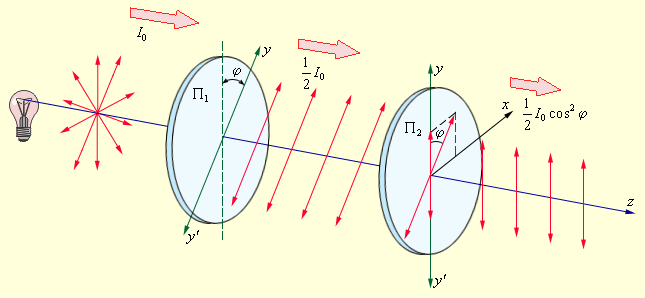
Відповідно до закону Малюса, інтенсивність I лінійно поляризованої хвилі на виході другого поляроїда буде дорівнює:

(1)

Виконання роботи.

1. Установити значення кута 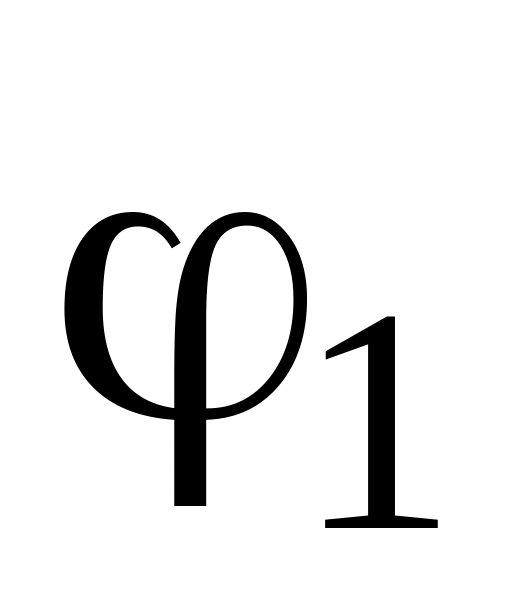відповідно до обраного варіанту.

Таблиця 1.

Варіант	1	2	3	4	5	6	7	8	9	10
,	–40	–30	–20	–10	0	10	20	30	40	50

2. Збільшуючи значення кута повороту другої пластини 2 від –90 до 90 через кожні 10 фіксувати значення кута =2–1 між площинами поляризації двох пластин та інтенсивність світла I, яке пройшло через обидві пластинки у частках інтенсивності природного світла. Результати вимірів занеси в таблицю 2:

Таблиця 2.

2 ,	-90	-80	-70	-60	-50	-40	-30	-20	-10	0	10	20	30	40	50	60	70	80	90
,
I

3. Побудувати графік залежності інтенсивності світла, що пройшло крізь пластинки, від кута . З графіка визначити, при яких кутах інтенсивність пройденого світла максимальна, а при яких мінімальна. Результати спів ставити з розрахунками за формулою (1) та зробити висновки.