
~
Индивидуальные задания
«Строительство» бакалавры (1-ый семестр)
Механика
Кинематика и динамика поступательного движения
 –
средняя
скорость;
–
средняя
скорость;
 – средняя
скорость вдоль траектории;
– средняя
скорость вдоль траектории;
 –
мгновенная
скорость;
–
мгновенная
скорость;
 –
величина
мгновенной скорости;
–
величина
мгновенной скорости;
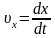 –
проекция
скорости на ось OX;
–
проекция
скорости на ось OX;
 –
среднее
ускорение;
–
среднее
ускорение;
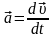 –
мгновенное
ускорение;
–
мгновенное
ускорение;
aх= –
проекция ускорения на осьOX;
–
проекция ускорения на осьOX;
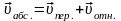 – закон
сложения скоростей;
– закон
сложения скоростей;
 и
и
 –
радиус-вектор и скорость материальной
точки при равнопеременном движении;
–
радиус-вектор и скорость материальной
точки при равнопеременном движении;
 – величина
тангенциального (касательного) ускорения;
– величина
тангенциального (касательного) ускорения;
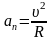 – величина
нормального (центростремительного)
ускорения;
– величина
нормального (центростремительного)
ускорения;
 – полное
ускорениепри криволинейном движении;
– полное
ускорениепри криволинейном движении;
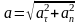 – модуль
полного ускорения;
– модуль
полного ускорения;
 ;
;
 (
( )
– второй закон Ньютона;
)
– второй закон Ньютона;
 – импульс тела;
– импульс тела;
 – третий закон Ньютона;
– третий закон Ньютона;
 – закон всемирного тяготения;
– закон всемирного тяготения;
 ;
;
 ;
;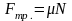 –
силы: тяжести, упругости и трения;
–
силы: тяжести, упругости и трения;
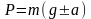 – вес тела;
– вес тела;
 - напряженность гравитационного поля;
- напряженность гравитационного поля;
 – плотность тела;
– плотность тела;
 – радиус-вектор центра масс.
– радиус-вектор центра масс.
Примеры решения задач
Задача 1.
Уравнение движения тела имеет вид x=5t+0.8t3. Определить проекциюскорости и ускорения тела на ось ОХ в начальный момент времени, а также среднее ускорение за первые 5 с движения.
Р ешение
ешение
Вектор скорости определяется соотношением:
,
а его проекция на ось ОХ – это производная
координаты
 по
времени
по
времени
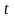 :
:
 .
(1)
.
(1)
Учитывая, что , получим
 .
(2)
.
(2)
Подставив в (1) и (2) t=0,
найдем скорость и ускорение в начальный
момент времени
 :
:
 =5
м/с,
=5
м/с,
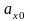 =0
м/с2.
=0
м/с2.
Среднее ускорение находим по определению
,
то есть
 ,
где скорость в момент времени t=5c
находим из (1):
,
где скорость в момент времени t=5c
находим из (1):
 .
.
Тогда величина среднего ускорения

Ответ:
=5
м/с;
=0
м/с2;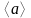 =12
м/с2.
=12
м/с2.
ИДЗ № 1
Тело брошено вертикально вверх с начальной скоростью 28 м/с. Определить наибольшую высоту и время подъема?
Зависимость координаты прямолинейно движущегося тела от времени дается уравнением x = 9t – 6t2 + t3 (координата – в метрах, время – в секундах). Найти зависимость скорости и ускорения от времени; путь, перемещение, скорость и ускорение тела через 2 секунды после начала движения.
Зависимость координаты тела, движущегося вдоль оси ОХ, от времени дается уравнением x = 16 – 9t2 + 2t3. Найти среднее значение модуля скорости и величину среднего ускорения тела в интервале времени от 1с до 4с.
Материальная точка движется прямолинейно вдоль оси ОХ. Уравнение ее движения имеет вид: x = 2 + 3t + 0.01t3 (координата – в метрах, время – в секундах). Найти скорость и ускорение материальной точки в начальный момент времени и через 10 сот начала движения?
Движение двух материальных точек описывается уравнениями:
x1 = 20 + 2t – 4t3 и x2 = 2 + 2t + 0.5t3 (координаты в метрах, время в секундах). В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?
Скорость тела выражается соотношением
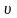 = 9 – t2.
Найти путьS
и модуль перемещения
= 9 – t2.
Найти путьS
и модуль перемещения
 тела через 10 сот начала движения.
тела через 10 сот начала движения.Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S=10+10t+0.5t2 (путь – в метрах, время – в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.
Материальная точка движется по окружности радиуса 80 см по закону S=10t–0.1t3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.
По дуге окружности радиуса 10 м движется материальная точка. В некоторый момент времени ее нормальное ускорение равно 5 м/с2, а вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 600. Найти скорость и тангенциальное ускорение данной точки.
Зависимость пройденного телом пути от времени дается уравнением S=A+Bt+Ct2+Dt3, где С=0.14 м/с2, D=0.01 м/с3. Через сколько времени после начала движения ускорение тела будет равно 1 м/с2? Чему равно среднее ускорение тела за этот промежуток времени?
Точка движется по окружности радиусом 2 см. Зависимость пути от времени дается уравнением S=0.1t3 (путь – в метрах, время – в секундах). Найти нормальное и тангенциальное ускорения точки в момент, когда линейная скорость точки равна 0.3 м/с.
Путь, пройденный материальной точкой, выражен уравнением S=Аt+Bt2. Найти скорость и ускорение точки через 10 с после начала движения, еслиА= 3 м/с, В = 1 м/с2.
Автомобиль движется по закруглению радиусом 500 м с тангенциальным ускорением 0,05 м/с2. Определить его нормальное и полное ускорение в тот момент, когда его скорость равна 5 м/с.
Космический корабль массой
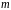 = 105
кг поднимается вертикально вверх, сила
тяги его двигателей
= 105
кг поднимается вертикально вверх, сила
тяги его двигателей
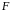 = 3∙106
Н. Чему равно его ускорение?
= 3∙106
Н. Чему равно его ускорение?Тело массой 2 кг движется прямолинейно, при этом зависимость пройденного пути от времени определяется законом
 ,
где все величины выражены в СИ. Найти
силу, действующую на тело в конце второй
секунды движения.
,
где все величины выражены в СИ. Найти
силу, действующую на тело в конце второй
секунды движения.Определить напряженность гравитационного поля
 на высоте
на высоте
 = 1000 м над поверхностью Земли.
= 1000 м над поверхностью Земли.Тело массой = 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути от времени дается уравнением
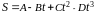 ,
где С = 5 м/с2,
D = 1 м/с3.
Найти величину силы, действующей на
тело в конце первой секунды движения.
,
где С = 5 м/с2,
D = 1 м/с3.
Найти величину силы, действующей на
тело в конце первой секунды движения.На брусок массой m = 5 кг в горизонтальном направлении действует сила F = 20 Н. Определить ускорение, с которым движется брусок, если коэффициент трения с горизонтальной поверхностью k = 0,4.
Определить скорость движения автомобиля перед торможением, если длина следа заторможенных колес оказалась равной
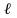 = 25 м. Коэффициент трения покрышек о
покрытие дороги k = 0,3.
= 25 м. Коэффициент трения покрышек о
покрытие дороги k = 0,3.Камень, пущенный по поверхности льда со скоростью 2 м/с, прошел до полной остановки расстояние 20.4 м. Найти коэффициент трения камня по льду.
Тело массой 0.5 кг движется прямолинейно, причем координата изменяется по закону x=A–Bt+5t2–t3 (время – в секундах, координата – в метрах). Найти силу, действующую на тело в конце первой секунды движения.
Брусок массой 200 г движется по горизонтальному столу под действием силы натяжения привязанной к ней нити. Нить перекинута через прикрепленный к столу блок и привязана к другому, падающему бруску массой 300 г. Определить силу натяжения нити, если коэффициент трения равен 0.25. Масса блока ничтожно мала.
Тело массой m = 100 кг поднимают по наклонной плоскости с ускорением
 = 2 м/с2.
Какую силу, параллельную наклонной
плоскости, необходимо приложить для
подъема тела. Коэффициент трения k =
0,2, угол наклона
= 300.
= 2 м/с2.
Какую силу, параллельную наклонной
плоскости, необходимо приложить для
подъема тела. Коэффициент трения k =
0,2, угол наклона
= 300.Тело массой m = 50 кг тянут равномерно по полу с помощью веревки, образующей угол = 300 с полом. Коэффициент трения k = 0,4. Определить силу, под действием которой движется тело.
Молекула массой
 кг,
летящая со скоростью 600 м/с, ударяется
о стенку сосуда под углом 600
к нормали и под таким же углом упруго
отскакивает от нее. Найти импульс силы,
полученный стенкой за время удара.
кг,
летящая со скоростью 600 м/с, ударяется
о стенку сосуда под углом 600
к нормали и под таким же углом упруго
отскакивает от нее. Найти импульс силы,
полученный стенкой за время удара.
