Контрольные вопросы

1. Какое влияние оказывает на результат опыта опоздание при закрытии крана?

2. Почему для газов различают несколько видов теплоемкостей?

3. От чего зависит теплоемкость?

4. Какова связь между удельной и молярной теплоемкостями?

5. Как практически осуществить адиабатический и изотермический процессы? Что это за процессы?

6. Вывести формулу: .

№4.Лабораторная работа изучение движения тел по наклонной плоскости.

Цель работы: Определить коэффициент трения стального шарика и цилиндра по дереву, а также проверка законов движения по наклонной плоскости на основе определения υ_т теоретической и экспериментальной υ_э скорости.

Приборы и принадлежности: наклонная плоскость, набор тел правильной формы, ящик с песком, отчетная линейка.

Для выполнения работы необходимо знать:

1. Теорию метода и описание установки.

2) Вывод формул: (1), где ; (2) где g - ускорение силы тяжести, h-высота наклонной плоскости, m-масса тела, R-радиус шара или цилиндра, k - коэффициент трения, x- расстояние от края стола до центра тяжести шара, упавшего на ящик с песком, у – расстояние от края стола до пола, α -угол, под которым наклонена плоскость к горизонтальной поверхности.

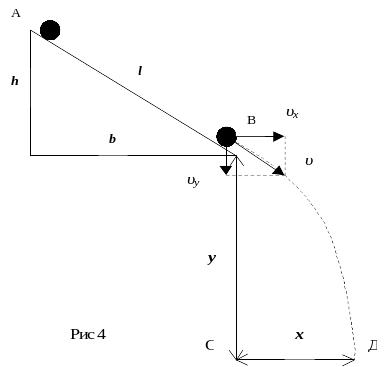
3. Закон движения тел по наклонной плоскости.

Теория метода и описание установки

Исследуемое тело (шар, сплошной цилиндр, полый цилиндр) в точке А обладает запасом потенциальной энергии E_p=mgh. В точке В тело приобрело кинетическую энергию поступательного движения и вращательного движения (рис 4).

По закону сохранения энергии: . В данной работе скорость υ тела в точке В находят экспериментальным путем и теоретически по формуле (1). Определить скорость тела теоретически можно из закона сохранения энергии и соотношения . Получим формулу: где . (R)- радиус испытуемого тела, w- его угловая скорость в точке В. При вычислении скорости следует брать момент инерции:

- для сплошного цилиндра.

- для тонкостенного полого цилиндра.

- для шара.

Подставляя значения I находят значения k для всех тел. Из формулы (1), зная высоту наклонной плоскости, определяют скорость υ_т.

Экспериментальное определение скорости проводят следующим образом. В точке В тело имеет скорость, проекции которой в горизонтальном и вертикальном направлениях равны: , (рис. 4). Отрезки х и у могут быть определены из законов поступательного движения. В нашем случае ;

(3); где х- горизонтальное перемещение СД тела, у- путь проходимый телом по вертикали ВС.

Время перемещения тела по СД и ВС одинаково и равно , отсюда искомая величина скорости (4). Из формулы (3) найдем время (5) и подставим в формулу (4). После подстановки получим окончательное выражение для определения скорости тела экспериментальным путем: .

Измерение и обработка результатов измерений.

1. Измеряют длину наклонной плоскости l, основание наклонной плоскости b, высоту подъема h, вычисляют cos α и tg α для трех случаев высоты h.

2. Измеряют радиусы образцов и пускают из точки А по наклонной плоскости. Измеряют расстояние х=СД для различных высот.

3. По формуле (2) подсчитывают скорости тел в точке В. Полученные значения сравнивают со значениями, вычисленными для тех же образцов по формуле (1). По формуле (5) находят время t для различных образцов.

4. Все вычисления записывают в таблицу.

№	Тело	h	b	x	cos α	tg α	y	υ э	υ т	k	f %
1. 2. 3.	шар
1. 2. 3.	цилиндр