Контрольные вопросы:

1. Объясните процесс теплопроводности с точки зрения молекулярно – кинетической теории.

2. Назовите все способы передачи теплоты. Объясните механизмы различных видов передач теплоты.

3. Что называется градиентом температуры?

4. Что такое коэффициент теплопроводности и в чем измеряется?

5. Для чего при измерениях необходимо перемешивать жидкость в сосуде калориметра?

6. Прочтите и запишите формулу уравнения теплопроводности.

7. Рассказать ход работы.

8. Вывести формулу:

9. Сделать выводы по работе

№2. Лабораторная работа

Определение ускорения силы тяжести.

Приборы и принадлежности: электросекундомер, выпрямитель, маятник, стальной шарик, секундомер, линейка.

Теоретическая часть:

1. Знать законы свободного падения.

2. Знать методы определения ускорения свободного падения

методом математического маятника.

3. Разобраться в принципе работы электросекундомера.

4. Уметь выводить формулы: и

I метод. Определение ускорения свободного падения электросекундомером.

Метод основан на законах движения свободно падающего шарика. Свободным падением называется движение тела без начальной скорости под действием только силы тяжести. Свободное падение – движение равноускоренное с постоянным ускорением, которое обозначается (g). Поэтому законы равноускоренного движения без начальной скорости: ; записываются для свободного падения: ; . Из формулы высоты находят значение , что используют для определения ускорения методом падающего шарика.

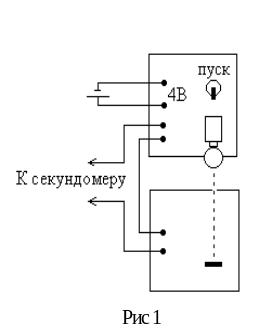
Для измерения времени падения пользуются установкой, собранной по схеме (рис 1). Электро-секундометр вибрационного типа имеет разгрузочное сопротивление (R) и рабочую катушку (К). Когда по катушке проходит ток, железный сердечник притягивается переменным полем, вибрирует и приводит в действие стрелку электро-секундомера. Большая стрелка показывает сотые доли, а малая стрелка целые секунды. Для остановки электросекундомера необходимо или отключить, или накоротко замкнуть рабочую катушку к клеммам электромагнита, или подъемом педали. Электромагнит, питаемый от выпрямителя, удерживает шарик возле своего сердечника. Он состоит из двух изолированных друг от друга половинок, служащих одновременно контактами для замыкания накоротко рабочей катушки. При включении тумблера цепь электромагнита, размыкается шарик падает и одновременно включается секундомер. Остановка происходит тогда, когда, ударяясь о педаль, шарик опускает её, замыкая тем самым накоротко рабочую катушку, смонтированную на передней педали электросекундомера.

II метод: Метод математического маятника.

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятник.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Хорошим приближением к математическому маятнику служит небольшой шарик, подвешенный на длинной тонкой нити. Отклонение маятника от положения равновесия будем характеризовать углом (φ), образованным нитью с вертикалью. При отклонении маятника от положения равновесия возникает вращательный момент (М), равный по величине (mglsinφ), (m- масса, l- длина маятника).

M=mglsinφ

Напишем для маятника уравнение динамики вращательного движения M=Iε. Угловое ускорение и, учитывая, что момент инерции маятника равен ml², получим:

ml²φ^//=-mglsinφ, приведем к виду: .

При малых колебаниях sin φ ≈ φ. Введем обозначение: , тогда получим . Следовательно, при малых колебаний угловые отклонения маятника изменяются со временем по гармоническому закону.

Известно, что с учетом того что , отсюда можно найти где l- длина маятника от точки подвеса до центра масс.

Центр массы шарика определяется путем дополнительных расчетов, которые приводят к увеличению погрешностей, чтобы избежать этого можно пользоваться формулой: которая получается, если записать период колебаний для длинного и короткого маятника и решить систему относительно g; ; .

В этом случае нас интересует только Δl, которую можно определить (измерить) как расстояние между двумя положениями любой точки шарика. Для определения периода колебания подсчитывают время n колебаний, затем, поделив общее время на число колебаний, находят период Т, время одного колебания. Если для обеих длин брать одинаковое число колебаний, то формулу для определения ускорения свободного падения можно записать: .