
Лекция 6.
§ 36. Линейная зависимость векторов. Линейная комбинация векторов. Коллинеарность векторов. Компланарность векторов.
Векторы
![]()
![]() …,
…,
![]() называются линейно зависимыми, если
существуют числа
называются линейно зависимыми, если
существуют числа
![]() ,
,
![]() ,
…
,
…
![]() ,
среди которых по крайней мере одно, не
равное нулю, такие, что
,
среди которых по крайней мере одно, не
равное нулю, такие, что
![]() .
.
Сумма
произведений чисел
![]() на векторы
на векторы
![]() ,
т.е. вектор
,
т.е. вектор
![]()
называется линейной комбинацией векторов .
Если
вектор
![]() представлен в виде линейной комбинации
векторов
,
то говорят также, что вектор
разложен по векторам
.
представлен в виде линейной комбинации
векторов
,
то говорят также, что вектор
разложен по векторам
.
Данное
выше определение линейной зависимости
векторов
![]() ,
эквивалентно такому: векторы
линейно зависимы, если один из них можно
представить в виде линейной комбинации
остальных (или разложить по остальным).
,
эквивалентно такому: векторы
линейно зависимы, если один из них можно
представить в виде линейной комбинации
остальных (или разложить по остальным).
Теорема
1.
Для того чтобы два вектора
![]() и
и
![]() были линейно зависимы, необходимо и
достаточно, чтобы они были коллинеарны.
были линейно зависимы, необходимо и
достаточно, чтобы они были коллинеарны.
Доказательство необходимости. Дано: векторы и линейно зависимы. Требуется доказать, что они коллинеарны. Так как векторы и линейно зависимы, то существуют числа и , не равные нулю одновременно, и такие, что
![]() .
.
Пусть,
например,
![]() ;
тогда
;
тогда
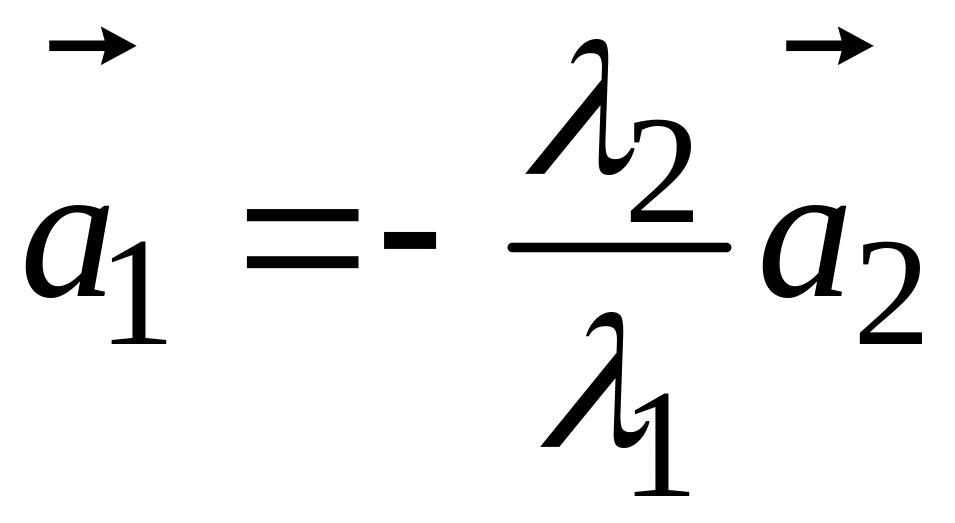 ;
;
отсюда следует, что векторы и коллинеарны.
Доказательство достаточности. Дано: векторы и коллинеарны. Требуется доказать, что они линейно зависимы.
Если
![]() ,
то имеет место равенство
,
то имеет место равенство
![]() ,
а это означает, что векторы
и
линейно зависимы
,
а это означает, что векторы
и
линейно зависимы
![]() .
.
Если
же
![]() ,
то полагая
,
то полагая
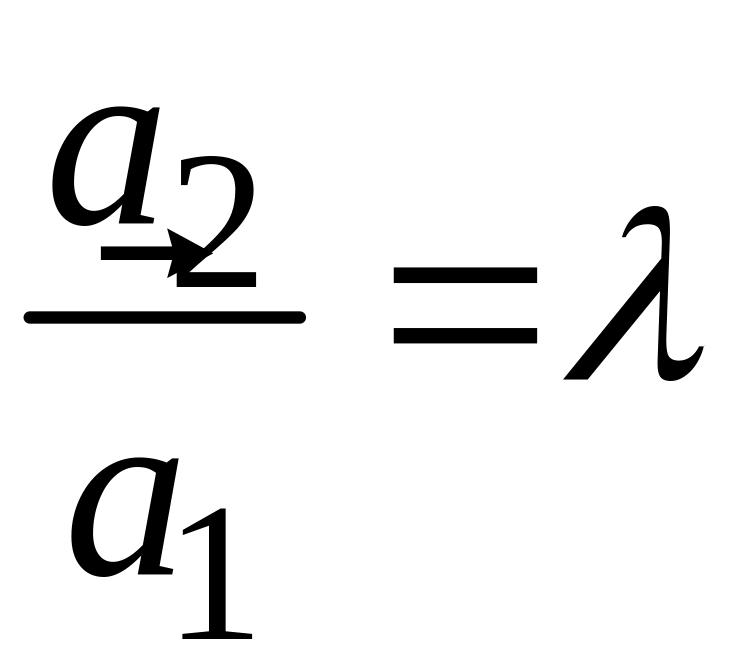 ,
находим
,
находим
![]() ,
или
,
или
![]() ;
значит векторы
и
линейно зависимы.
;
значит векторы
и
линейно зависимы.
Три вектора называются компланарными, если, будучи отложены от одной точки, оказываются лежащими в одной плоскости.
Теорема
2.
Для того, чтобы три вектора
,
,
![]() были линейно зависимы, необходимо и
достаточно, чтобы они были компланарны.
были линейно зависимы, необходимо и
достаточно, чтобы они были компланарны.
Доказательство необходимости. Дано: векторы , , линейно зависимы. Требуются доказать, что они компланарны.
Так как
векторы
,
,
линейно зависимы, то существуют числа
,
,
![]() ,
среди которых есть хотя бы одно
,
среди которых есть хотя бы одно
![]() ;
такие, что
;
такие, что
![]() .
.
Пусть,
например,
![]() ;
тогда
;
тогда
 .
.
Векторы
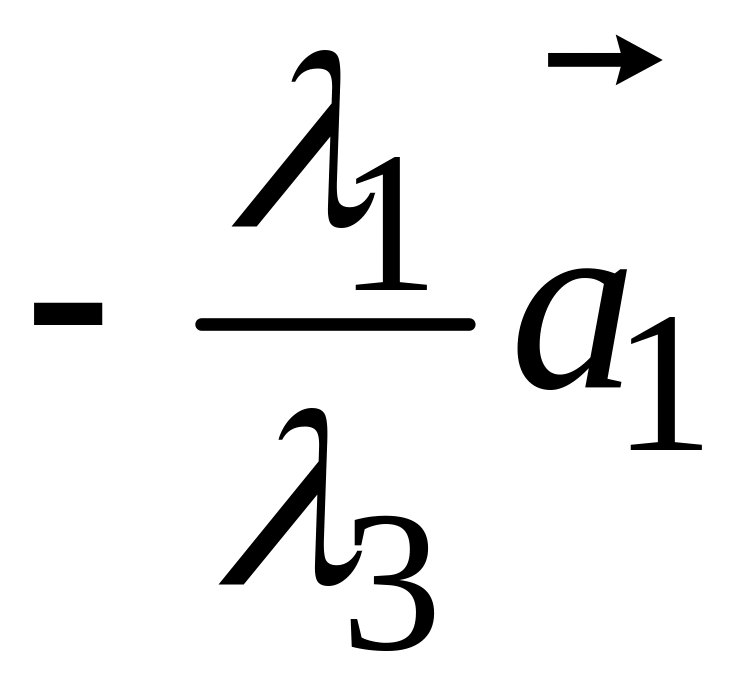 и
и
 коллинеарны соответственно векторам
и
;
поэтому сумма таких векторов, т.е. вектор
коллинеарны соответственно векторам
и
;
поэтому сумма таких векторов, т.е. вектор
![]() будет компланарен с векторами
и
.
будет компланарен с векторами
и
.
Доказательство достаточности. Дано: векторы , , компланарны. Требуется доказать, что эти векторы линейно зависимы.
 Если
векторы
и
коллинеарны, то они линейно зависимы
(теорема 1 настоящего параграфа), т.е.
найдутся числа
и
,
из которых по крайней мере одно не равно
нулю и такие, что
,
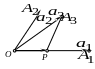
но тогда и
Если
векторы
и
коллинеарны, то они линейно зависимы
(теорема 1 настоящего параграфа), т.е.
найдутся числа
и
,
из которых по крайней мере одно не равно
нулю и такие, что
,
но тогда и
![]() ,
т.е. векторы
,
,
линейно зависимы.
,
т.е. векторы
,
,
линейно зависимы.
Пусть векторы и неколлинеарны. Отложим векторы , и от одной и той же точки О:
![]() .
.
Так как
векторы
,
,
компланарны, то точки О,
![]() лежат в одной плоскости. Спроектируем
точку
лежат в одной плоскости. Спроектируем
точку
![]() на прямую
на прямую
![]() параллельно прямой
параллельно прямой
![]() ;
пусть Р
– эта проекция. Тогда
;
пусть Р
– эта проекция. Тогда
![]() и так как
и так как
![]() и
,
и
,
![]() и
и
![]() ,
,
то, полагая
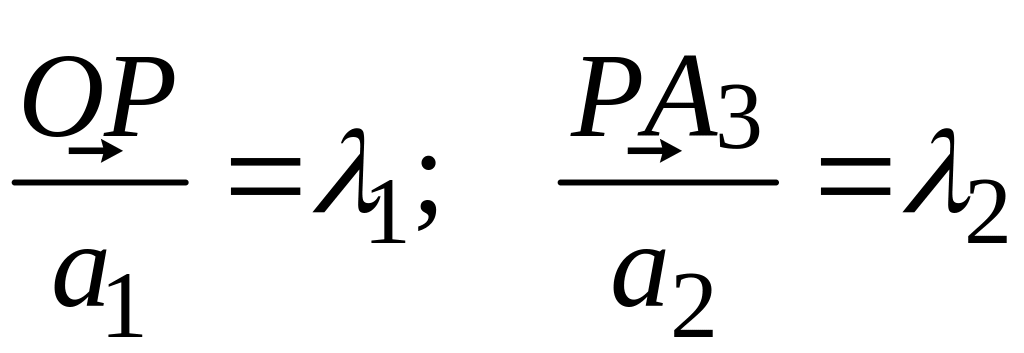 ,
,
находим
![]() ,
,
так что
![]() ,
,
то есть векторы , , - линейно зависимы.
Теорема
3.
Всякие четыре вектора
,
,
,
![]() в пространстве линейно зависимы.
в пространстве линейно зависимы.
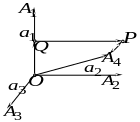 Доказательство.
Предложим, то векторы
,
,
некомпланарны. Отложим все векторы
,
,
,
от одной и той же точки О:
Доказательство.
Предложим, то векторы
,
,
некомпланарны. Отложим все векторы
,
,
,
от одной и той же точки О:
![]()
![]()
![]()
![]() .
(см.рис)
.
(см.рис)
Пусть
Р
– проекция точки
![]() на плоскость
на плоскость
![]() параллельно прямой
параллельно прямой
![]() ,
а
,
а
![]() - проекция точки Р
на прямую
параллельно прямой
.
Тогда
- проекция точки Р
на прямую
параллельно прямой
.
Тогда
![]() .
.
Векторы
![]() соответственно коллинеарны векторам
,
и
.
Полагая
соответственно коллинеарны векторам
,
и
.
Полагая
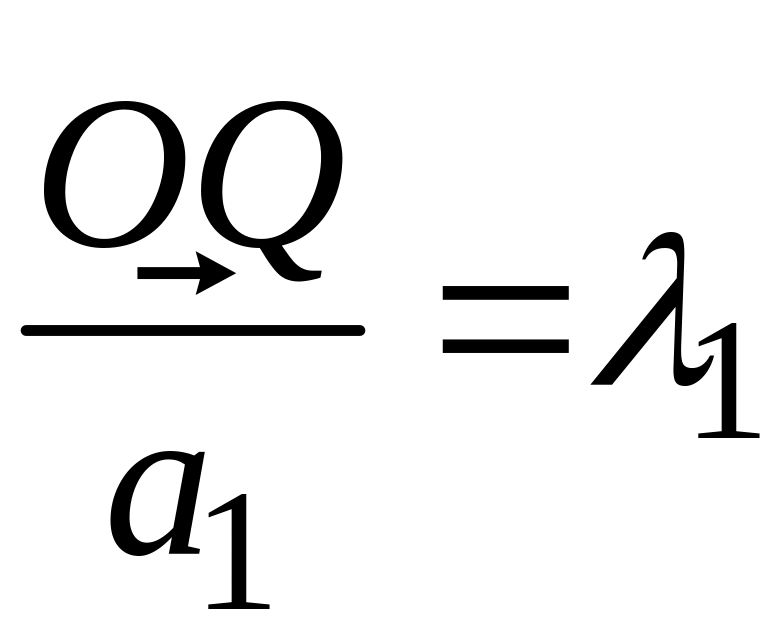 ;
;
 ;
;
 получим
получим
![]() ;
;
![]() ;
;
![]()
и, следовательно:
![]() ,
,
т.е. векторы , , , линейно зависимы.
Теорема 4. Для того, чтобы два ненулевых вектора и были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.
Докажем теорему для случая, когда векторы заданы своими координатами относительно общей декартовой системы координат в пространстве.
Доказательство
необходимости.
Дано: векторы
![]() ;
и
;
и
![]() коллинеарны. Требуется доказать, что
их координаты пропорциональны.
коллинеарны. Требуется доказать, что
их координаты пропорциональны.
Так как
,
то полагая
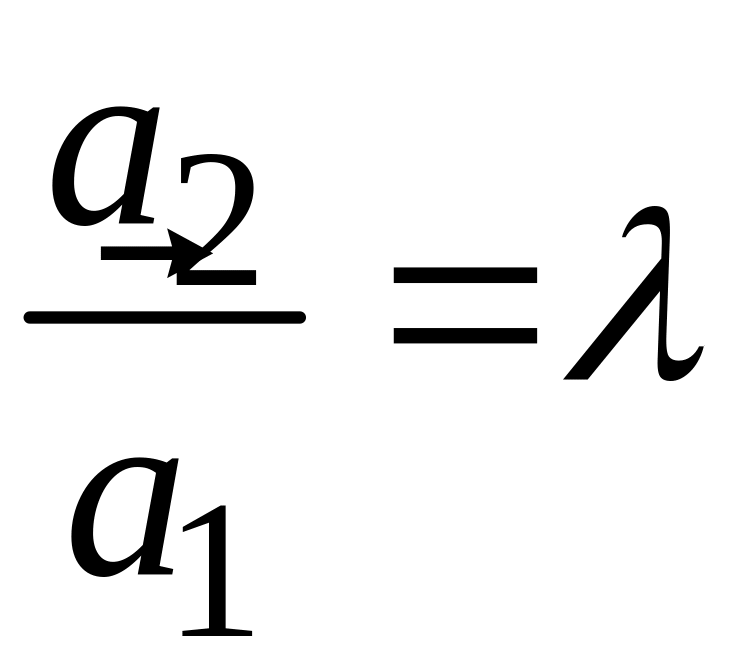 ,
получим
,
т.е.
,
получим
,
т.е.
![]() ,
,
или
![]() .
Ч.т.д.
.
Ч.т.д.
Доказательство достаточности. Дано: координаты векторов
и
пропорциональны. Требуется доказать, что эти векторы коллинеарны.
Пусть
;
то есть
![]() ,
или
,
и, значит, векторы
и
коллинеарны.
,
или
,
и, значит, векторы
и
коллинеарны.
Теорема 5. Для того, чтобы два вектора и , заданные своими координатами относительно общей декартовой системы координат на плоскости
![]() ,
,
![]()
или относительно общей декартовой системы координат в пространстве
;
были коллинеарны, необходимо и достаточно, чтобы
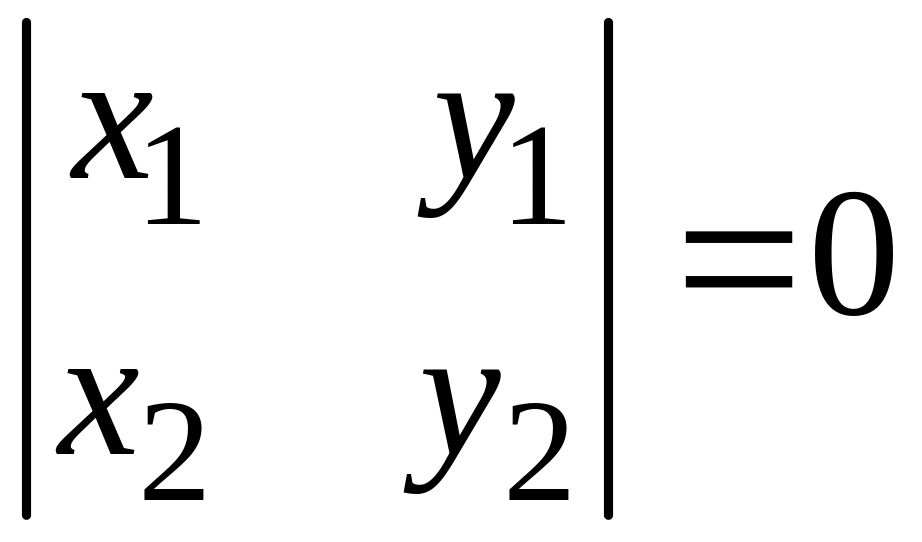 (в случае
плоскости),
(в случае
плоскости),
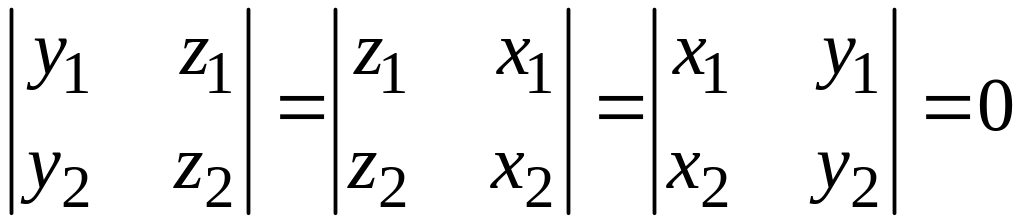 (в случае
пространства).
(в случае
пространства).
Докажем теорему для случая, когда векторы и заданы своими координатами относительно общей декартовой системы координат в пространстве.
Доказательство необходимости. Дано: векторы и коллинеарны. Требуется доказать, что выполнены соотношения
.
Если
векторы
и
ненулевые и коллинеарны, то их координаты
пропорциональны, а потому эти равенства
выполнены (определитель, в котором две
строки пропорциональны, равен нулю).
Если
или
![]() (или
=
=0),
то это равенство очевидно.
(или
=
=0),
то это равенство очевидно.
Доказательство достаточности. Дано, что эти соотношения выполнены. Требуется доказать, что векторы и коллинеарны.
Если
![]() (т.е.
=0),
то векторы
и
коллинеарны (т.к. нулевой вектор
коллинеарен любому вектору). Пусть хотя
бы одно из чисел
(т.е.
=0),
то векторы
и
коллинеарны (т.к. нулевой вектор
коллинеарен любому вектору). Пусть хотя
бы одно из чисел
![]() не равно нулю, например
не равно нулю, например
![]() .
Положим
.
Положим
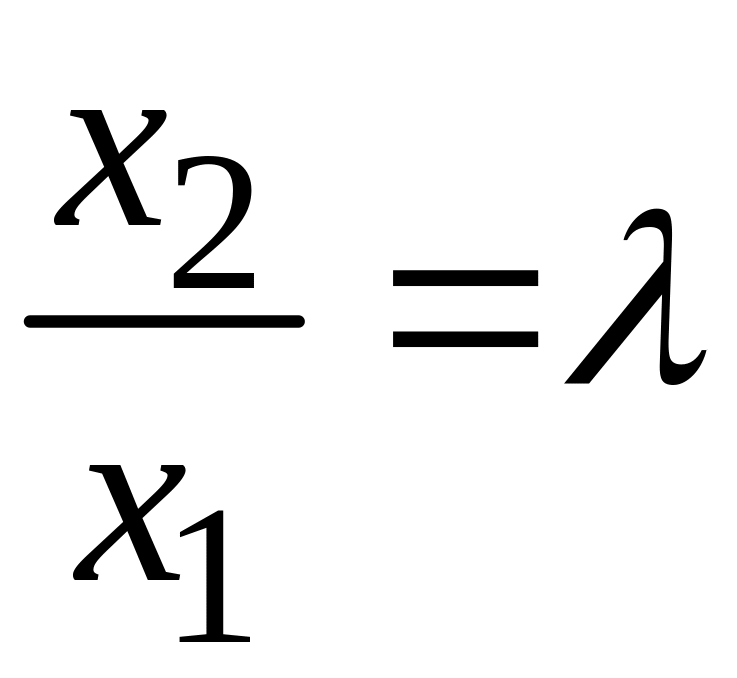 ;
тогда
;
тогда
![]() и из соотношения
и из соотношения
 или (раскрывая определитель)
или (раскрывая определитель)
![]() ,
находим
,
находим
![]() ,
,
и так
как
имеем
![]() ,
т.е.
,
т.е.
![]() .
.
Аналогично из соотношения
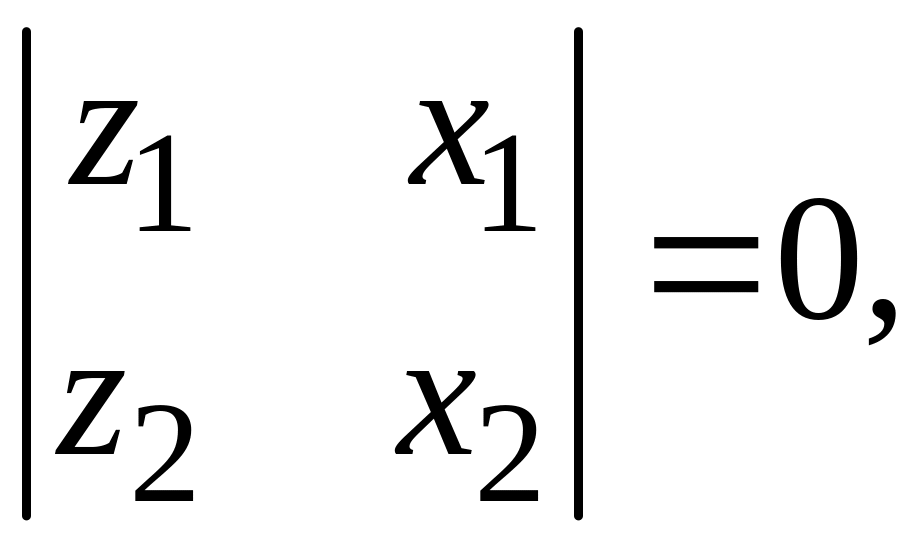 или
или
![]() ,
находим:
,
находим:
![]() ,
,
и так
как
,
то
![]() т.е.
т.е.
![]() .
.
Итак, или ,
т.е. векторы и коллинеарны.
Теорема 6. Необходимым и достаточным условием компланарности трех векторов
![]() заданных
своими координатами относительно общей
декартовой системы координат, является
равенство
заданных
своими координатами относительно общей
декартовой системы координат, является
равенство
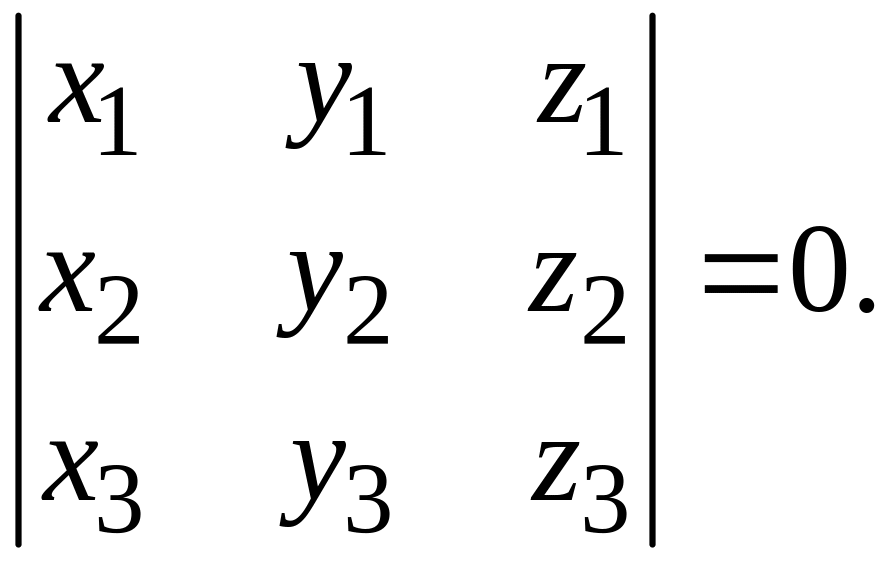
Доказательство. На основании предыдущей теоремы векторы , , будут компланарны тогда и только тогда, когда найдутся три числа , , , не равные нулю одновременно, такие, что
,
или
![]() ,
,
или
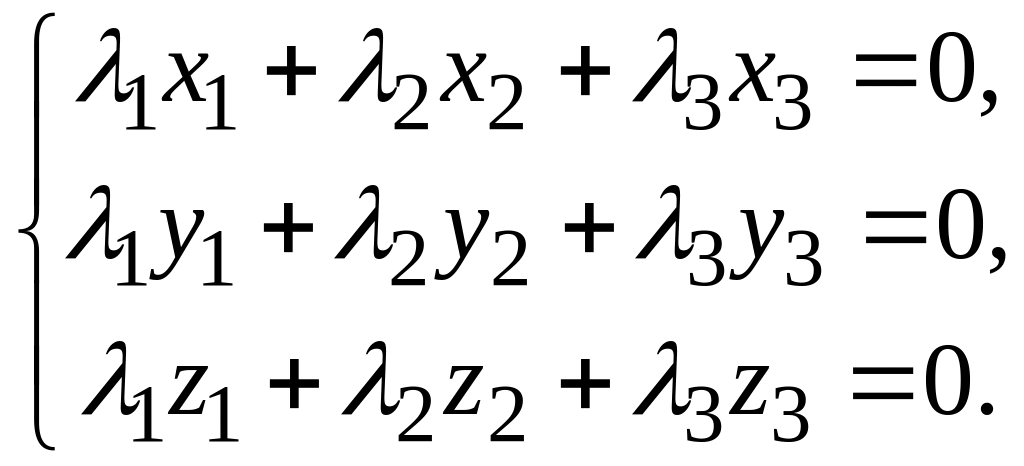
Эта
система соотношений относительно
![]() линейная и однородная. Но для того, чтобы
линейная однородная система n
уравнений с n
неизвестными имела ненулевое решение,
(т.е. решение, в котором хотя бы одно из
неизвестных не равно нулю), необходимо
и достаточно, чтобы определитель этой
системы был равен нулю, то есть чтобы
определитель системы равнялся нулю.
линейная и однородная. Но для того, чтобы
линейная однородная система n
уравнений с n
неизвестными имела ненулевое решение,
(т.е. решение, в котором хотя бы одно из
неизвестных не равно нулю), необходимо
и достаточно, чтобы определитель этой
системы был равен нулю, то есть чтобы
определитель системы равнялся нулю.
Это и доказывает нашу теорему.
Из доказанных теорем вытекают такие следствия.
Следствие
1.
Три попарно различные точки
![]() ,
,
![]() ,
,
![]() ,
заданные своими координатами относительно
общей декартовой системы координат на
плоскости, лежат на одной прямой тогда
и только тогда, когда векторы
,
заданные своими координатами относительно
общей декартовой системы координат на
плоскости, лежат на одной прямой тогда
и только тогда, когда векторы
![]() и
и
![]() коллинеарны, т.е. тогда и только тогда,
когда их координаты пропорциональны:
коллинеарны, т.е. тогда и только тогда,
когда их координаты пропорциональны:
 или
или
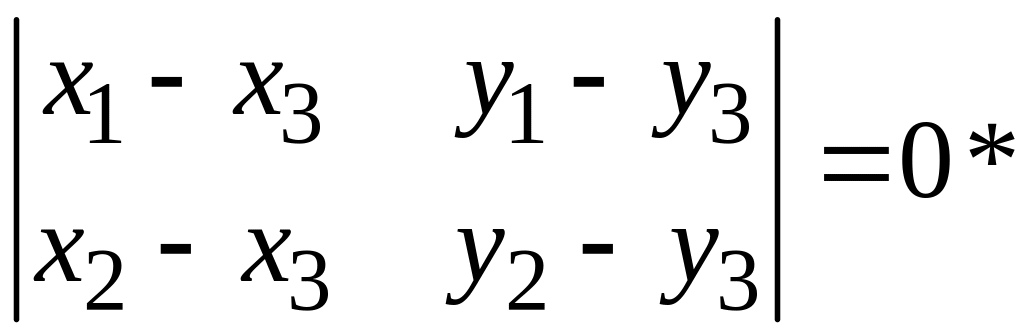 .
.
![]() среди
этих точек могут быть и совпадающие.
среди
этих точек могут быть и совпадающие.
Следствие
2.
Три попарно различные точки
![]() ,
,
![]() ,
,
![]() ,
заданные своими координатами относительно
общей декартовой системы координат в
пространстве, принадлежат одной прямой
тогда и только тогда, когда выполнены
соотношения
,
заданные своими координатами относительно
общей декартовой системы координат в
пространстве, принадлежат одной прямой
тогда и только тогда, когда выполнены
соотношения
 ,
,
или
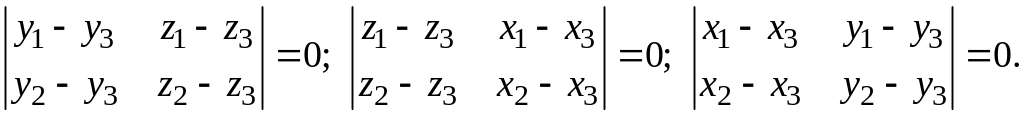
Следствие
3.
Точки
,
,
,
![]() ,
заданные своими координатами относительно
общей декартовой системы координат в
пространстве, принадлежат одной плоскости
тогда и только тогда, когда векторы
,
заданные своими координатами относительно
общей декартовой системы координат в
пространстве, принадлежат одной плоскости
тогда и только тогда, когда векторы
![]() ;
;
![]() ;
;
![]() компланарны, т.е. тогда и только тогда,
когда
компланарны, т.е. тогда и только тогда,
когда
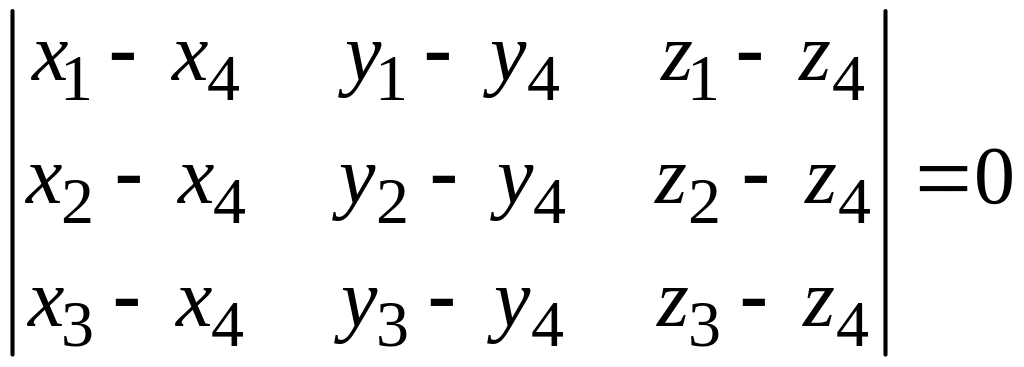 .
.
