2.3.Интервалы выпуклости и вогнутости, точки перегиба

Достаточные условия выпуклости и вогнутости графика функции.

Если функция дважды дифференцируема на промежутке X и f (x) < 0 для всех xX, то график функции на X выпуклый, если f (x) > 0, то график функции на X вогнутый.

Общая граничная точка промежутков выпуклости и вогнутости графика функции называется точкой перегиба этой функции (графика функции).

Если ─ точка перегиба графика функции , то выполняется одно из следующих условий:

1) ,

2) ,

3) не существует.

Но сама функция в точке в двух последних случаях должна быть непрерывной.

Достаточное условие точки перегиба.

Точка является точкой перегиба графика функции, если производная второго порядка при переходе через точку меняет знак.

Пример 12. Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции .

Решение.

Производная второго порядка равна нулю в точке . Других точек, в которых равна 0, или не существует, нет.

На интервале (–; 3) график функции выпуклый, а на интервале (3; +) – вогнутый (f (x) < 0). Точка x = 3; y = –2·e³ является точкой перегиба графика функции.

Пример 13. Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции .

Решение.

Производная второго порядка равна в точке . Сама функция в этой точке непрерывна.

В интервале график функции выпуклый ( ), а в интервале график функции вогнутый ( ). Точка (3; 1) является точкой перегиба графика функции.

Пример 14. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции .

Решение.

Производная второго порядка

равна нулю в точке , равна в точке , не существует в точке (f (1–0) = 4, f (1+0) = –4, f (1–0) ≠ f (1+0))

Точки x = 0, x = 1, x = 3, являются такими точками, при переходе через которые вторая производная может изменить знак. Установим интервалы выпуклости и вогнутости графика функции.

	(–; 0)	(0; 1)	(1; 3)	(3; +)
	+	+	─	+
	Вогнутая	Вогнутая	Выпуклая	Вогнутая

Точка не может быть точкой перегиба, так как в ней функция не определена.

При x = 1 вторая производная не существует, но сама функция непрерывна в ней. Точка является точкой перегиба графика функции, так как при переходе через точку вторая производная меняет знак.

Точка (3; 2/9) является точкой перегиба графика функции: при x = 3 вторая производная равна нулю и меняет знак при переходе через эту точку.

Пример 15. Найти интервалы выпуклости и вогнутости, точки перегиба графика функции .

Решение.

Вторая производная функции в точке равна , но функция в этой точке непрерывна. Производная второго порядка отрицательна как при , так и при . Функция не имеет точек перегиба, так как является выпуклой на всей области определения.

2.4.Схема исследования функции

При исследовании функции следует выполнить следующие операции:

1. найти множество определения функции, выделить точки разрыва;

2. исследовать поведение функции в окрестностях граничных точек множества определения, определить типы разрыва;

3. найти асимптоты графика функции;

4. проверить наличие свойств четности, нечетности, периодичности;

5. найти нули функции;

6. выделить интервалы монотонности, найти экстремумы функции;

7. выделить интервалы выпуклости и вогнутости, указать точки перегиба.

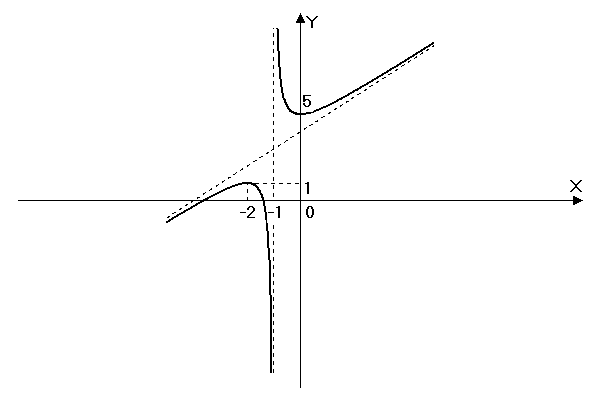
Пример 16. Исследовать функцию и построить ее график.

Решение.

1. Множество определения функции X=

2. .

х = 1 ─ точка бесконечного разрыва (точка разрыва второго рода).

3. ─ наклонная асимптота, ─ вертикальная асимптота (см. пример 7).

4. Функция не является ни четной, ни нечетной;

Функция не является периодической.

5. .

6. , .

– интервал возрастания функции,

– интервал убывания функции,

– интервал убывания функции,

– интервал возрастания функции (см. пример 8).

7. 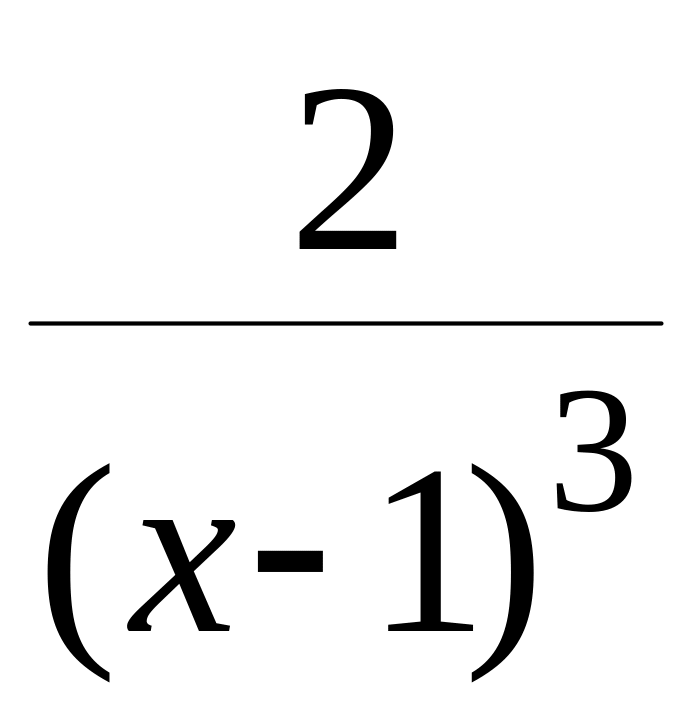равна при Но эта точка не может быть точкой перегиба графика функции, так как в ней функция не определена.

В интервале (–; 1) функция выпуклая ( ), в интервале (1; +) функция вогнутая ( ).

Пример 17. Исследовать функцию и построить ее график.

Решение.

1. Множество определения функции X = .

2. Точек разрыва функции нет.

3. ,

.

─ горизонтальная асимптота.

Вертикальных асимптот график функции не имеет.

4. . Функция не является ни четной, ни нечетной (f(–x) ≠ f(x); f(–x) ≠ –f(–x)). Функция не является периодической.

5. Нулей функции нет.

6.  . Производная функции равна нулю в точках

	─	0	+	0	─
	Убывает		Возрастает		Убывает

Интервалами монотонности функции являются:

.

,

.

7. .

В точках x = 0; x = 3; x = 6 производная второго порядка равна нулю.

	Выпуклая		Вогнутая		Выпуклая		Вогнутая
	─	0	+	0	─	0	+

Точки ─ точки перегиба графика функции.

Пример 18. Исследовать функцию и построить ее график.

Решение.

1. Множество определения функции X = 

2  , . х = –1 ─ точка бесконечного разрыва (точка разрыва второго рода).

3. ,

.

─ наклонная асимптота;

─ вертикальная асимптота.

4. Функция не является ни четной, ни нечетной. Функция не является периодической.

5. при ; .

6. . Производная функции равна нулю в точках х = –2 и х = –0.

Точка ─ не является критической точкой, так как в этой точке функция не определена. Таким образом, критическими точками этой функции являются точки х = –2 и х = –0. Интервалами монотонности функции являются: (–; –2), (–2; –1), (–1; 0), (–1; +).

	(–; –2)	–2	(–2; –1)	–1	(–1; 0)	0	(–1; +)
	+	0	─		─	0	+
	Возрастает	1	Убывает		Убывает	5	Возрастает

, .

7. Вторая производная функции равна в точке .

Эта точка не может быть точкой перегиба графика функции, так как в ней функция не определена.

	─		+
	Выпуклая		Вогнутая