
- •1.1. Непрерывность функции в точке и на множестве
- •1.2.Точки разрыва функции и их классификация
- •Пример 3
- •Пример 4
- •2. Исследование функций и построение их графиков
- •2.1. Асимптоты графика функции
- •2.2.Экстремумы функции, интервалы монотонности.
- •2.3.Интервалы выпуклости и вогнутости, точки перегиба
- •2.4.Схема исследования функции
- •Список рекомендуемой литературы
Пример 4

Решение.
Функция определена
на X
=
![]() .
.
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
и
,
и
 ,
т.е.
,
т.е.![]() и непрерывна.
и непрерывна.
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
и
,
и
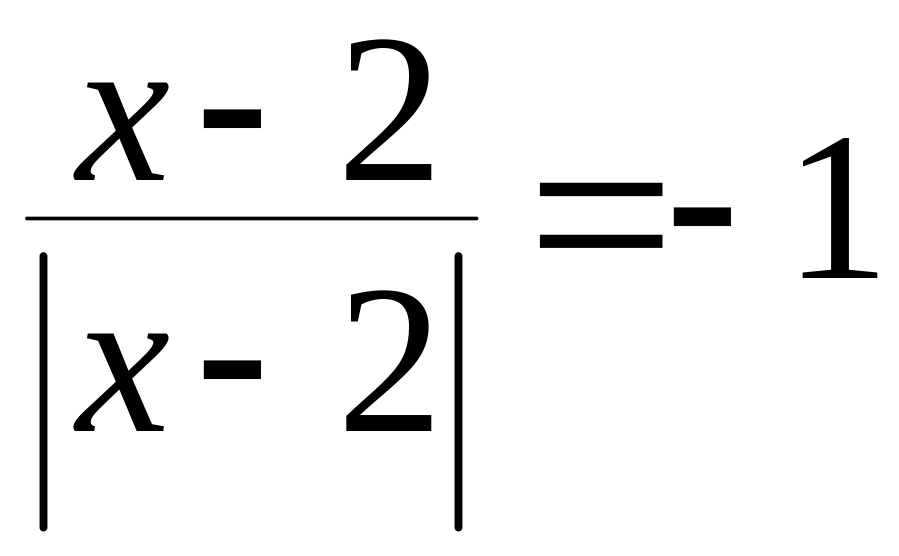 ,
т.е.
,
т.е.![]() и непрерывна.
и непрерывна.

Найдем односторонние пределы в точке .
![]()
![]()
Так как пределы слева и справа конечны, но не равны между собой, то в точке функция имеет разрыв I рода (конечный).
График этой функции представлен ниже.

2. Исследование функций и построение их графиков
2.1. Асимптоты графика функции
1. Прямая
![]() является наклонной
асимптотой
графика функции
является наклонной
асимптотой
графика функции
![]() ,
если существуют конечные пределы
,
если существуют конечные пределы


При
![]() асимптота называется горизонтальной.
асимптота называется горизонтальной.
2. Прямая
![]() является вертикальной
асимптотой
графика функции
,
если хотя бы один из пределов
является вертикальной
асимптотой
графика функции
,
если хотя бы один из пределов
![]() или
или
![]() равен
равен
![]() или
или
![]() .
.
Пример 5. Найти наклонные асимптоты графика функции
![]()
Решение.
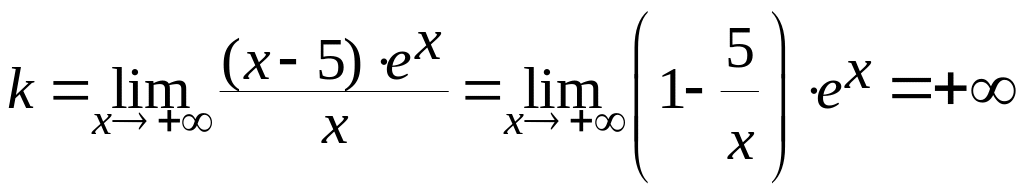 ,
следовательно, при
,
следовательно, при
![]() наклонная асимптота отсутствует.
наклонная асимптота отсутствует.
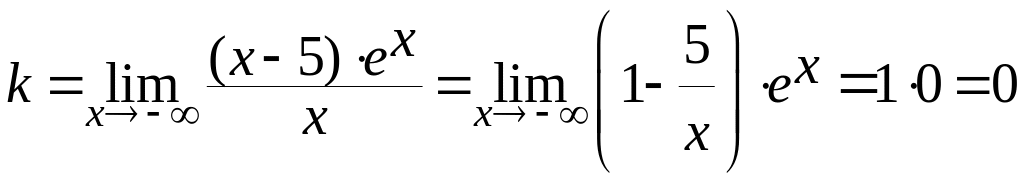 ,
,
 .
.
Имеем
![]() ,
значит,
,
значит,
![]() ─ горизонтальная асимптота при
─ горизонтальная асимптота при
![]() .
.
Пример 6.
Найти асимптоты
графика функции
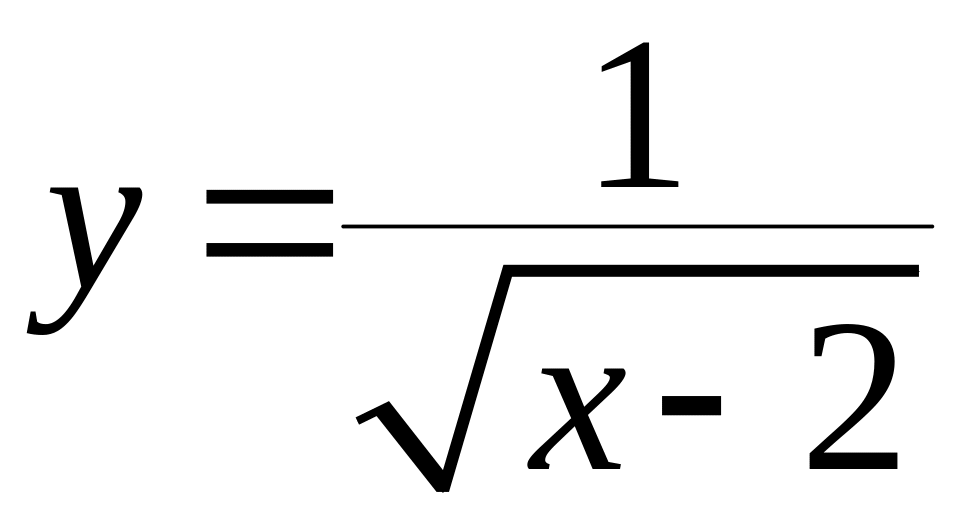 .
.
Решение.
 Следовательно,
─ горизонтальная асимптота при
Следовательно,
─ горизонтальная асимптота при
![]() .
.
При наклонной асимптоты не существует, так как при функция не определена.
Прямая является вертикальная асимптотой, так как
 .
.
Пример 7.
Найти асимптоты
графика функции
![]() .
.
Решение.
 Следовательно,
Следовательно,
![]() ─ наклонная асимптота.
─ наклонная асимптота.
Прямая
![]() является вертикальной асимптотой, так
как
является вертикальной асимптотой, так
как
 .
.
2.2.Экстремумы функции, интервалы монотонности.
Пусть функция исследуется на некотором промежутке X (конечном или бесконечном).
Если для любых х1, х2 X выполняется
![]() ,
то функция называется возрастающей на
X.
,
то функция называется возрастающей на
X.
Если для любых х1, х2 X выполняется
![]() ,
то функция называется убывающей на X.
,
то функция называется убывающей на X.
Если для любых х1, х2 X выполняется
![]() ,
то функция называется неубывающей на
X.
,
то функция называется неубывающей на
X.
Если для любых х1, х2 X выполняется
![]() ,
то функция называется невозрастающей
на X.
,
то функция называется невозрастающей
на X.
Возрастающие, убывающие, неубывающие, невозрастающие функции называются монотонными функциями на X.
Если функция
дифференцируема на промежутке
![]() и f (x) > 0
на этом промежутке, то она возрастает
на
;
если f (x) < 0,
то функция убывает. Если
и f (x) > 0
на этом промежутке, то она возрастает
на
;
если f (x) < 0,
то функция убывает. Если
![]() во всех точках промежутка
,
то она постоянна на этом промежутке.
во всех точках промежутка
,
то она постоянна на этом промежутке.
Точка
![]() называется точкой
максимума
функции
,
если существует окрестность
называется точкой
максимума
функции
,
если существует окрестность
![]() этой точки такая, что
этой точки такая, что
xR(x0), x≠ x0 : f (x) < f (x0) .
Точка называется точкой минимума функции , если существует окрестность этой точки такая, что
xR(x0), x≠ x0 : f (x) > f (x0) .
Значения функции
в точках ее максимума и минимума
называются, соответственно, максимумом
и минимумом функции и обозначаются
![]() и
и
![]() .
.
Максимумы и минимумы функции называются экстремумами или экстремальными значениями этой функции.
Критическими
точками
функции
называются точки, в которых или
,
или
![]() ,
или
,
или
![]() не
существует, но в двух последних случаях
функция должна быть непрерывна в
соответствующей точке.
не
существует, но в двух последних случаях
функция должна быть непрерывна в
соответствующей точке.
Необходимое условие экстремума.
Для того чтобы была точкой экстремума функции , необходимо, чтобы она была критической точкой этой функции.
Достаточные условия экстремума.
1. Пусть
─ критическая точка функции
.
Если в некоторой окрестности
этой точки
![]() при
при
![]() и
и
![]() при
при
![]() ,
то
,
то
![]() .
.
Если в некоторой
окрестности
этой точки
при
и
при
,
то
![]() .
.
2. Пусть в некоторой окрестности критической точки функция дважды дифференцируема и производная второго порядка функции в этой окрестности непрерывна.
Если
![]() ,
то
;
,
то
;
если
![]() ,
то
;
,
то
;
если
![]() ,
то требуется дополнительное исследование
по производным более высокого порядка.
,
то требуется дополнительное исследование
по производным более высокого порядка.
Пример 8.
Найти экстремумы
и интервалы монотонности функции
 .
.
Решение.
Производная функции
 равна нулю в точках
равна нулю в точках
![]() и равна
и равна
![]() в точке
.
в точке
.
В точке функция имеет бесконечный разрыв. Значит, критическими точками этой функции являются точки .
Производная второго
порядка
![]()
 .
.
![]() – отрицательна, значит, f(0) = max f (x).
– отрицательна, значит, f(0) = max f (x).
В точке
производная второго порядка положительна
(![]() ),
значит, f
(2) = min
f(x).
),
значит, f
(2) = min
f(x).
В точке разрыва функции производная первого порядка может изменить знак, поэтому она включается во множество точек, которые разбивают множество определения функции на интервалы монотонности.
Установим, как ведет себя функция в соответствующих интервалах монотонности.
-





+
─
─
+
Возрастает
Убывает
Убывает
Возрастает
Интервалами монотонности функции являются (–, 0); (0, 1); (1, 2); (2, +). При переходе через точки и производная первого порядка меняет знак на противоположный. Таким образом, существование экстремумов функции в этих точках подтвердил и первый достаточный признак.
Пример 9.
Найти точки экстремума функции
![]() .
.
Решение.
В точке
производная функции
не существует, так как при
![]()
![]() ,
а при
,
а при
![]()
![]() .
Сама же функция в точке
непрерывна. Эта точка является критической
точкой функции. Других критических
точек у функции нет. При переходе через
точку
производная
меняет знак с “─” на “+”, значит, в
этой точке функция принимает наименьшее
значение и f
(0) = min
f(x).
График функции
приведен ниже на рисунке.
.
Сама же функция в точке
непрерывна. Эта точка является критической
точкой функции. Других критических
точек у функции нет. При переходе через
точку
производная
меняет знак с “─” на “+”, значит, в
этой точке функция принимает наименьшее
значение и f
(0) = min
f(x).
График функции
приведен ниже на рисунке.
|
Пример
10. Найти
точки экстремума функции
![]() .
.
Решение.
В точке
производная функции
 не существует. Сама функция в этой точке
непрерывна. Значит, эта точка является
критической точкой функции. Других
критических точек у функции нет. При
переходе через точку
производная первого порядка меняет
знак, так как
при x < 0,
а при положительных значениях аргумента
.
Следовательно,
является точкой минимума. График функции
в окрестности точки
изображен ниже.
не существует. Сама функция в этой точке
непрерывна. Значит, эта точка является
критической точкой функции. Других
критических точек у функции нет. При
переходе через точку
производная первого порядка меняет
знак, так как
при x < 0,
а при положительных значениях аргумента
.
Следовательно,
является точкой минимума. График функции
в окрестности точки
изображен ниже.
|
Пример 11.
Найти точки
экстремума функции
![]() .
.
Решение.
В точке
производная функции
![]() равна 0. Других критических точек у
функции нет. Производная не принимает
отрицательных значений и при переходе
через точку
знака не меняет. Следовательно, в этой
точке достаточное условие экстремума
не выполняется, и
не является точкой экстремума. Ниже
изображен график этой функции.
равна 0. Других критических точек у
функции нет. Производная не принимает
отрицательных значений и при переходе
через точку
знака не меняет. Следовательно, в этой
точке достаточное условие экстремума
не выполняется, и
не является точкой экстремума. Ниже
изображен график этой функции.
|
Наибольшее
(наименьшее) значение непрерывной
функции на замкнутом промежутке
![]() достигается или
в экстремальных точках, или на концах
этого промежутка.
достигается или
в экстремальных точках, или на концах
этого промежутка.



