Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

дифференциальные уравнения.doc

Скачиваний:

Добавлен:

11.11.2019

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 77

§7. Пример выполнения контрольной работы

Задача1. Найти общее решение (общий интеграл) уравнения

Решение. Уравнение записано в дифференциальной форме и после элементарных преобразований приводится к виду

Сравнивая полученное уравнение с (2.5), убеждаемся, что задача1 – уравнение с разделяющимися переменными. (§2,пункт 2). Разделяя переменные, имеем

Проинтегрировав последнее уравнение, окончательно получим

Задача2. Найти общее решение уравнения

Решение. Уравнение записано в обычной, недифференциальной форме. Поделив обе части уравнения на , получим

Сравнивая полученное выражение c (2.13), убеждаемся, что уравнение является линейным (§2, пункт4).

, .

Решение ищем в виде .

Из (2.17) получим уравнение для нахождения функции v

Разделяя переменные, имеем . Интегрируя, находим или .

Подставляя найденное в (2.18), получаем уравнение для определения

Разделяя переменные и интегрируя, находим

Окончательно, общее решение исходного уравнения имеет вид

Задача3. Найти решение уравнения

удовлетворяющее начальному условию .

Решение. Уравнение записано в недифференциальной форме. Очевидно, что его нельзя привести к виду (2.8), (2.13), (2.14), то есть уравнение не является однородным, линейным и Бернулли. Перейдем к дифференциальной форме записи (2.2). Для этого заменим на , умножим обе части уравнения на и все перенесем в левую часть. В результате имеем

Очевидно, что это уравнение является уравнением с разделенными переменными(§2, пункт 1). Интегрируя, находим общее решение в неявном виде (общий интеграл)

Подставляя из начального условия в последнее соотношение и , получим, что . Окончательно решение задачи Коши в неявной форме имеет вид

Задача4. Найти решение уравнения

удовлетворяющее начальному условию .

Решение. Уравнение записано в дифференциальной форме, но с помощью элементарных преобразований его нельзя привести к виду (2.5). Следовательно, уравнение не является уравнением с разделяющимися переменными. Проверим, не является ли оно уравнением в полных дифференциалах (§2, пункт 5).

, .

Найдем частные производные

, .

Таким образом, , и уравнение является уравнением в полных дифференциалах.

Дифференцируя последнее выражение по , получим

С другой стороны,

Приравнивая правые части полученных равенств, находим

или .

Тогда . Полагая и подставляя в выражение для функции , находим

Общий интеграл имеет вид

Подставляя в последнее уравнение из начального условия и , находим, что . Тогда решение уравнения, удовлетворяющее начальному условию, имеет вид

Задача5. Методом неопределённых коэффициентов найти решение уравнения , удовлетворяющее начальным условиям .

Решение. Общее решение можно записать в виде , где - общее решение соответствующего однородного уравнения, а - некоторое частное решение данного уравнения. Характеристическое уравнение имеет вид . Оно имеет два равных вещественных корня , и, следовательно, общее решение соответствующего однородного уравнения примет вид . Правая часть исходного уравнения является многочленом второй степени. Число λ = 0 не является корнем характеристического уравнения, значит, частное решение данного дифференциального уравнения будем искать в виде многочлена второй степени с неопределёнными коэффициентами . Для того, чтобы найти эти коэффициенты, вычислим и , а затем подставим их в исходное уравнение. Итак, . При подстановке в уравнение получим . Сгруппируем по степеням х: . Приравнивая друг другу коэффициенты при одинаковых степенях х в правой и левой частях равенства, получим систему трех уравнений с тремя неизвестными 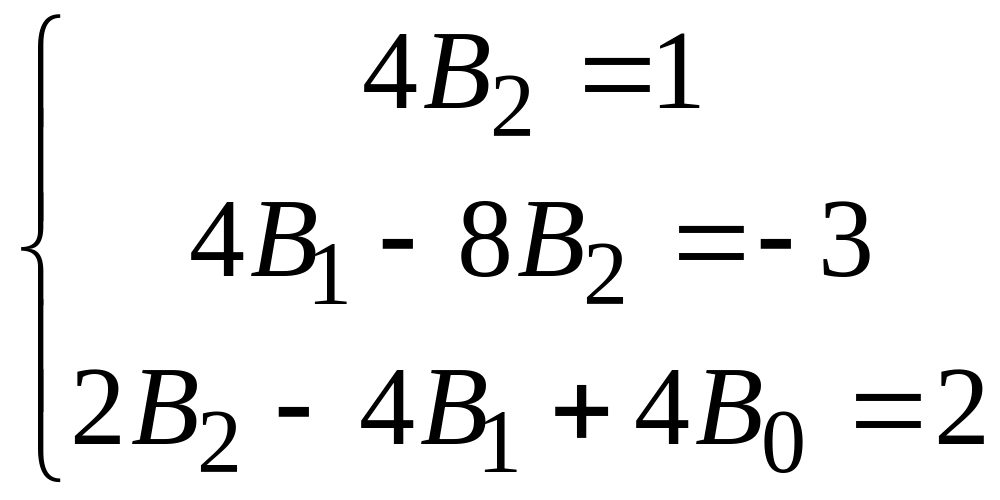, решив которую, найдём значения 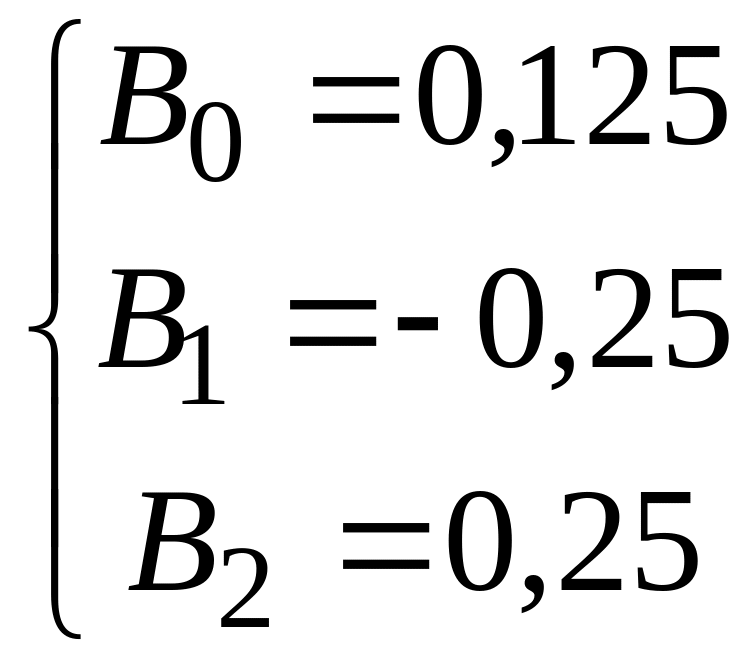. Таким образом, , а общее решение исходного уравнения есть . Теперь чтобы определить значения , воспользуемся начальными условиями , предварительно продифференцировав найденное решение: . Получим систему , решив которую, найдём значения . Окончательно получаем частное решение данного дифференциального уравнения, удовлетворяющее заданным начальным условиям в виде .

Задача6. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям , двумя способами: а) методом неопределённых коэффициентов; б) операционным методом.

Решение методом неопределённых коэффициентов. Общее решение можно записать в виде , где - общее решение соответствующего однородного уравнения, а - некоторое частное решение данного уравнения. Характеристическое уравнение имеет вид . Оно имеет два разных вещественных корня , и, следовательно, общее решение соответствующего однородного уравнения примет вид . Правая часть исходного уравнения является экспонентой. Число λ = 1 не является корнем характеристического уравнения, значит, частное решение данного дифференциального уравнения будем искать в виде , где А - неопределённый коэффициент. Вычислим производные, а затем подставим их в исходное уравнение. Итак, . При подстановке в уравнение получим , то есть , откуда легко видеть, что А = -1/9. Таким образом , а общее решение исходного уравнения есть . Теперь чтобы определить значения , воспользуемся начальными условиями , предварительно продифференцировав найденное решение . 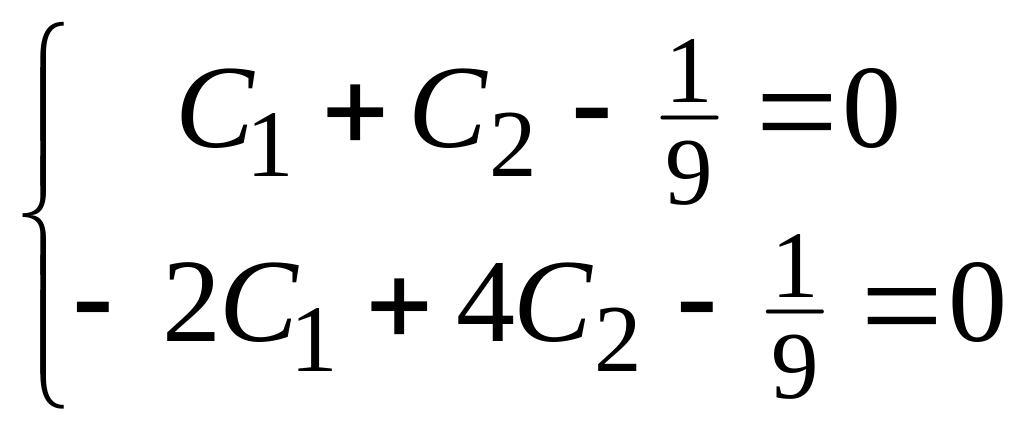Получим систему , решив которую, найдём значения . Частное решение данного дифференциального уравнения, удовлетворяющее заданным начальным условиям, примет вид .

Решение операционным методом. Обозначим через решение исходного уравнения, удовлетворяющее заданным начальным условиям, а через его изображение. Тогда . Так как у нас , то . По таблице изображений находим и составляем вспомогательное уравнение или , откуда получаем . Представим полученную дробь в виде суммы простейших дробей с неопределёнными коэффициентами

Приравнивая числители, получим соотношение для определения коэффициентов

Теперь если задать , то получим ,

если задать , то получим ,

если задать , то получим .

Итак, . Пользуясь таблицей изображений, находим решение .

Задача 7. Найти решение уравнения , удовлетворяющее условию , на отрезке с шагом .

Решение. Используем приближенный метод Эйлера (§6).

, , , , ,

Используя (6.3) , находим

Вычисления удобно представить в виде таблицы


0	0	0,5	1,05
1	0,1	0,547619	1,104762
2	0,2	0,593074	1,164069
3	0,3	0,636552	1,227724
4	0,4	0,678219	1,295546
5	0,5	0,718219	1,367368
6	0,6	0,75668	1,443036
7	0,7	0,793717	1,522408
8	0,8	0,829431	1,605351
9	0,9	0,863914	1,691742
10	1	0,897247	1,781467