Лабораторная работа №5 истечение жидкости через 0тверстия и насадки

Цель работы: экспериментальное определение коэффициентов скорости при истечении воды через отверстия и насадки.

Теоретические основы работы.

Рассмотрим случай вытекания жидкости в атмосферу через круглое отверстие площадью ω из емкости, заполненной этой жидкостью, и также сообщенной с атмосферой (рис. 1).

При подходе жидкости к отверстию ее частицы движутся по криволинейным траекториям. Так как частицы жидкости обладают инерцией, то при выходе из отверстия струя сжимается на расстоянии от стенки сосуда L₀ =d_отв/2 площадь сеченая струи достигает своего минимального значения ω_стр (сечение С-С).

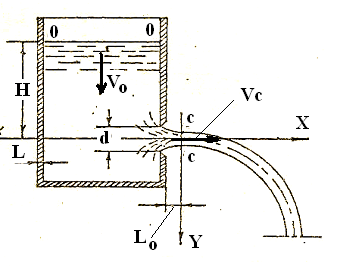
Рис.1. Схема истечения жидкости через отверстие в тонкой стенке.

Отношение

ε = ω_стр / ω (1)

называется коэффициентом сжатия струи. Для круглого отверстия ε = 0,64.

Если горизонтальная ось Х проходит через центр тяжести отверстия, тогда уравнение Бернулли, записанное для сечения 0-0 и сжатого сечения С-С, будет иметь вид:

H + (V_O²/2g) = (V_C²/2g) + h_М (2)

где:

V_O - скорость жидкости в сосуде в м/с;

h_М - потеря напора при вытекании жидкости через отвер­стие в м;

V_C - средняя скорость жидкости в сечении С-С в м/с.

Потеря напора h_М относится к числу местных потерь и определяется по формуле:

h_М = ξ(V_C²/2g) (3)

где ξ - коэффициент местного сопротивления.

Пренебрегая величиной (V_O²/2g) ввиду её малости по сравнению с величиной Н, получаем

H = (V_C²/2g)(1 + ξ) (4)

Откуда

V_C=(1 + ξ)^-0,5(2gH)^0,5 (5)

Коэффициент

φ =(1 + ξ)^-0,5 (6)

называется коэффициентом скорости. По опытным данным значение коэффициента скорости для круглого отверстия в стенке сосуда φ = 0,97.

Расход жидкости, вытекающей из отверстия, может быть определён, как

Q_cтр= V_C ω_стр (7)

Учитывая, что ω_стр = ω ε, находим

Q_cтр= εφω(2gH)^0,5 (8)

Величина

μ=εφ (9)

называется коэффициентом расхода. Для круглого отверстия

μ=0,64 ^.0,97=0,62.

Обозначим толщину стенки сосуда через L (см. риc.1), а диаметр отверстия через d. Если (L/d)<3, то стенку рассматривают как тонкую, а отверстие называют отверстием в тонкой стенке. При вытекании жидкости через такое отверстие потери напора являются местными. Если (L/d)> 3, то такое отверстие рассматривается уже как короткая трубка, вставленная в отверстие. Короткие трубки называются насадками. Они могут герме­тически присоединяться к кромкам отверстия в тонкой стенке и иметь различные формы. При гидравлическом расчете такой короткой трубки можно пренебречь потерями напора по длине, а учитывать только местные потери напора.

В инженерной практике используют разнообразные насадки. Например, конические сходящиеся насадки применяют в том случае, когда нужно получить компактную струю, обладающую кинетической энергией в бьющую на большое расстояние. Такие насадки исполь­зуют в пожарных брандспойтах, в гидромониторах для размыва грунта, в соплах активных гидравлических турбин, Конические расходящиеся насадки приводят к торможению и распылению струи. Они используются для замедления течения жидкости в отсасывающих трубах гидравлических турбин, при вводе жидкости из трубопровода в резервуар, для предупреждения удара струи о стенку, для распыла топлива в двигателях внутреннего сгорания и т.д.

При течении жидкости через насадок любой формы, кроме конусоидального, внутри него вблизи входа образуется сжатое сечение, струи, затем струя расширяется, заполняет насадок целиком и на входе либо не сжимается (например, для насадка Вентури.), либо сжимается очень слабо. При истечении в атмосфе­ру, в сжатом сечении насадка образуется вакуум. Наличие его приводит к увеличению расхода жидкости при истечении через насадок по сравнению с истечением из отверстия.

Значения коэффициентов истечения приведены в таблице 1.

Таблица 1.

Коэффициенты истечения через отверстия и насадки.

№	Вариант истечения	ε	ξ	φ	μ
1	Отверстие в тонкой стенке	0,64	0,06	0,97	0,62
	Через цилиндрическую насадку:
2	внешнюю (Вентури)	1	0,49	0,82	0,82
3	внутреннюю	1	1	0,71	0,71
4	Через насадок со скруглёнными входными кромками	1		0,98	0,98
	Через конический насадок с углом раскрытия β:
5	сходящуюся β=0,07π	0,98	0,06	0,97	0,95
6	расходящуюся β=0,04π	1	3,94	0,45	0,45

Длина насадка L_Н ограничивается следующими пределами;

(3,5-4,0)D < L_Н < (6,0-7,0)D (10)

где D - диаметр отверстия насадка.

При L_Н<(3,5-4,0)D длина насадка может оказаться недостаточной для расширения транзитной струи после сжатия на входе, т. е. возможен "проскок" струи через насадок (отрыв от боковых стенок трубы).

При L_Н >(6,0-7,0)D потеря напора по длине соизме­рима с местными потерями, т.е имеет место случай "короткого" трубопровода, когда необходимо учитывать, как местные потери, так и потери напора по длине.

Основные расчетные зависимости для насадков имеют тот же вид, что и для случая истечения жидкости из отверстия

V= φ_Н(2gH)^0,5 (11)

где V - средняя скорость жидкости в выходном сечении насадка в м/с;

φ_Н= (1 + ξ_Н)^-0,5 - коэффициент скорости насадка;

ξ_Н - полный коэффициент сопротивления наездка, который учитывает все потери капора внутри насадка. Так, например, для насадка Вентури (см. рис. 3.), коэффициент потерь складывается из трех членов, а именно, из коэффициентов потерь при входе в насадок (до сжатого сечения струи), при расширении струи и по всей длине насадка:

ξ_Н = ξ_вх + ξ_расш + λ(L_Н/ D) (12)

Таким образом

Q= V ω= μ_Н ω(2gH)^0,5 (13)

Уравнение траектории струи, свободно падающей после истечения из отверстия в тонкой стенке (рис, 1), может быть найдено на основании следующих соображений. Пусть в центре сжатого сечения C-С располагается начало координатных осей X и Y. Тогда положение материальной точки, которая имела в начале координат скорость V_C, определяется следующими уравнениями:

X= V_Cτ; Y=gτ²/2 (14)

где τ – время в секундах.

Решая совместно уравнения (14) и (5) получим:

φ= X/(2(НY)^0,5) (15)

Следовательно, при известных значениях X, Y и Н для струи можно определить значения коэффициента скорости. Для конкретных случаев истечения величины X и Y опреде­ляются опытным путем для какой-либо точки траектории струи.