1.2.4 Логические элементы и схемы. Принцип двойственности.

До этого мы нечего не говорили о структуре логического устройства представляя его в виде черного ящика. Однако ФАЛ однозначно определяет его внутреннюю структуру логического устройства. Если мы располагаем элементарными устройствами реализующие логические операции, заданные ранее, то с их помощью можно построить логическую схему, выполняющую заданный алгоритм преобразования исходных логических переменных. Характер реальных логических переменных не имеет значения и может быть произвольным.

В соответствии с перечнем логических операций различают три основных логических элемента: И, ИЛИ, НЕ. Условные графические обозначения этих

элементов показаны на рис 1.3.

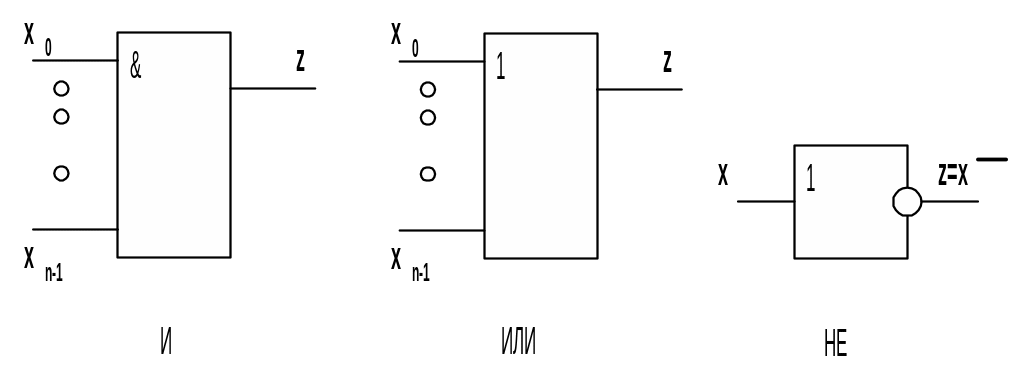
Рис.1.3

Число входных элементов может быть произвольным. Элемент НЕ имеет всегда один вход.

Для построения логической схемы необходимо ЛЭ, предназначенные для выполнения логических операций, указанных в ФАЛ, располагать от входа в порядке, определенном булевым выражением.

Пример: 1.7 Построить структурную схему логического устройства по ФАЛ из примера 1.5.

Решение: Структурная схема логического устройства, реализующего заданную ФАЛ, показана на рис.1.4.

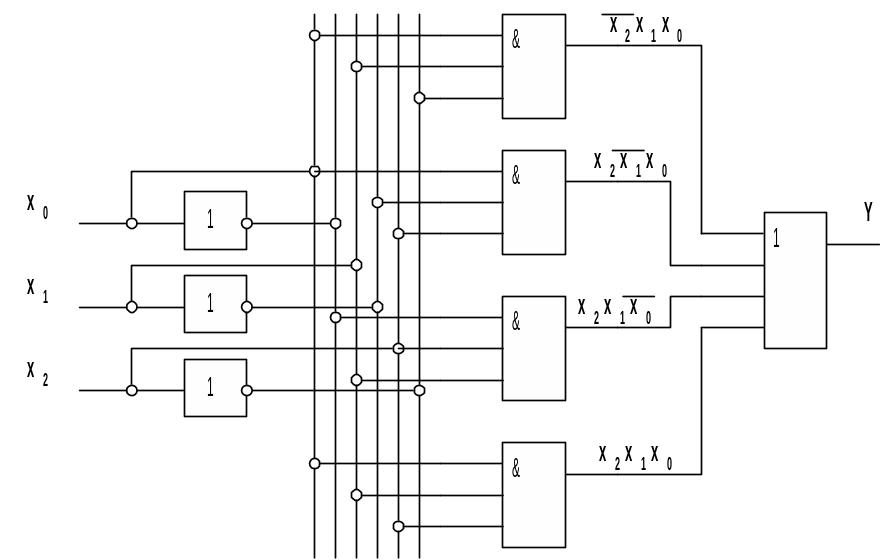
Рис.1.4 структурная схема логического устройства (пример 1.7)

Рис.1.5 Условные графические обозначения элементов 2И-НЕ и 2ИЛИ-НЕ

При сравнении таблиц истинности для операций И и ИЛИ легко заметить, что если в условиях, определяющих операцию И, значения всех переменных и самой функции заменить инверсией, а знак логического умножения – знаком логического сложения, получим постулаты, определяющие операцию ИЛИ:

Если то

Если то

Это свойство взаимного преобразования постулатов операций логического сложения и умножения носит название принципа двойственности.

Практическим следствием принципа двойственности является тот факт, что при записи логических выражений и при построении схем, можно обойтись только двумя типами операций, например И и НЕ или ИЛИ и НЕ.

Существует понятие функционально полной системы ЛЭ. Функционально полной системой называется совокупность ЛЭ, позволяющих реализовать логическую схему произвольной сложности. Таким образом системы двух элементов И и НЕ, ИЛИ и НЕ также как и система трех элементов И, ИЛИ, НЕ являются функционально полными. На практике это элементы И-НЕ и ИЛИ-НЕ которые носят название штрих Шеффера и Стрелка Пирса. По определению каждый из этих элементов образует функционально полную систему. Их условные графические обозначения приведены на рис 1.5.

В качестве примера рассмотрим выполнение операций И, ИЛИ, НЕ на элементах ИЛИ-НЕ. Согласно принципу двойственности логическая операция И может быть заменена операциями ИЛИ и НЕ. На рис 1.6 приведены примеры реализации основных логических операций, с использованием только элементов ИЛИ-НЕ. Аналогично можно показать выполнение логических операций с использованием только элемента И-НЕ.

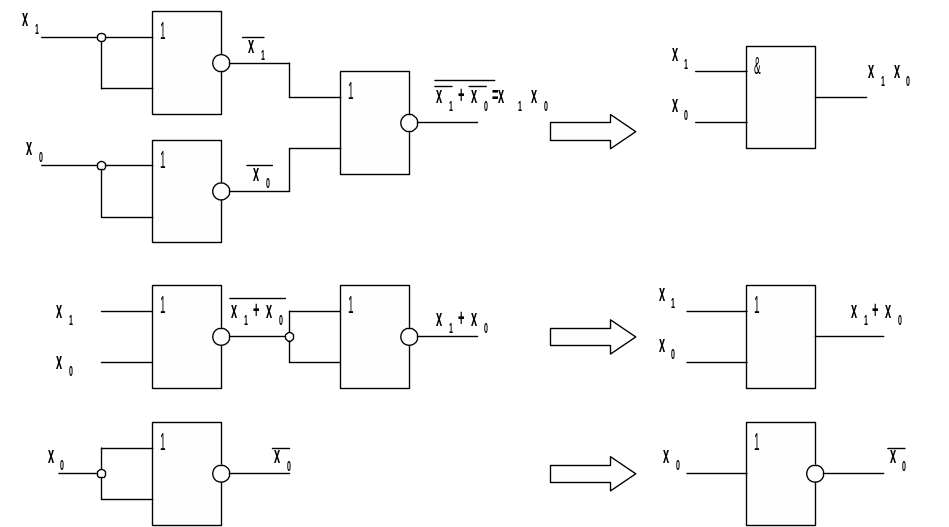
Рис.1.6 Реализация основных логических операций И, ИЛИ, НЕ на базе

элементов 2ИЛИ-НЕ