1.2.2 Логические константы и переменные. Операции булевой алгебры.
Для описания работы цифровых устройств необходим соответствующий математически аппарат. Такой аппарат для решения задач формальной логики в середине прошлого века разработал ирландский математик Д.Буль. По его имени математический аппарат и получил название булевой алгебры или алгебры логики. Булева алгебра - это математический аппарат оперирующий двумя понятиями: событие истинно и событие ложно. Булевые выражения могут принимать только два значения: Х=0 если Х=1, Х=1 если Х=0.
Определим множество операций, выполняемых над булевыми константами и переменными, а также постулаты, которым они удовлетворяют. Основными операциями булевой алгебры являются операции логического сложения, умножения и отрицания.
Логическое сложение. Эту операцию называют операцией ИЛИ или дизъюнкцией. Операция ИЛИ соответствует математической операции объединения множеств.
Таблица 1.3
Таблица истинности операции логического сложения.
Х1 |
Х2 |
Х1+Х0 |
0 0 1 1 |
0 1 0 1 |
0 1 1 1 |
Логическое умножение: Эту операцию называют операцией И или конъюнкцией. Она соответствует математической операции пересечения множеств.
Таблица 1.4
Таблица истинности операции логического умножения.
Х1 |
Х2 |
Х1+Х0 |
0 0 1 1 |
0 1 0 1 |
0 0 0 1 |
Отрицание: Операцию отрицания называют инверсией или дополнением. Для ее обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами
если Х=1 то Х=0
если Х=0 то Х=1
1.2.3 Способы записи функций алгебры логики.
Рассмотрим некоторое логическое устройство, на выходе которого присутствует некоторый n-разрядный двоичный код Xn-1...X1X0, а на выходе соответственно m - разрядный двоичный код Zm-1...Z1Z0.
Для того чтобы описать поведение этой схемы, необходимо определить зависимость каждой из m выходных переменных Zi от входного двоичного кода Xn-1...X1X0.
Зависимость выходных переменных Zi, выражения через совокупность входных переменных Xn-1..X1X0 с помощью операции алгебры логики, носит название функции алгебры логики (ФАЛ). Задать ФАЛ это значит определить значение Zi для всех возможных комбинаций переменных Xi-1...X1X0. Очевидно, что для n- разрядного двоичного кода Xn-1...X1X0 существует 2n различных значений Zi.
Ф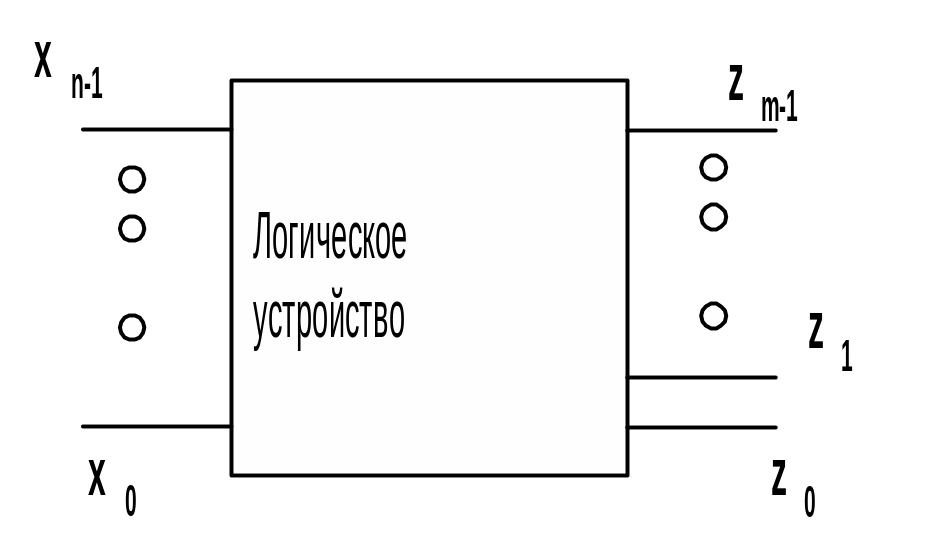
ункция
называется полностью определенной,
если заданны 2n ее значений. Если
часть значений функции на заданна, то
она называется частично определенной
или недоопределенной. Иногда по
условиям работы появление некоторых
входных кодов невозможно, поэтому
значения ФАЛ на этих кода не задаются.
При этом возникаю так называемые
Факультативные или необязательные
значения функции, которые могут быть
произвольными. Входные коды, для которых
ФАЛ не имеет значений, называются
запрещенными.
Рис.1.3 Обобщенная схема логического устройства
Для описания ФАЛ могут быть использованы различные способы.
Словесное описание ФАЛ. Словесное описание ФАЛ проиллюстрируем на примере.
Пример:1.3 Логическая функция трех переменных равна единице, если хотя бы две входные переменные равны единице.
Данный вид описания применяется для первоначального описания поведения логического устройства.
Описание ФАЛ в виде таблицы истинности: Таблица содержит все возможные комбинации входных переменных и соответствующие им значения выходных переменных. В общем случае таблица содержит 2n строк и m+n столбцов.
Пример: 1.4 Составить таблицу истинности для ФАЛ из примера 1.3.
Решение: Данная таблица имеет четыре столбца и восемь строк.
Таблица 1.5
Таблица истинности для трех переменных.
X2 |
X1 |
X0 |
Y |
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 0 0 1 0 1 1 1 |
Описание ФАЛ в виде алгебраического выражения. При описании ФАЛ алгебраическим выражением используют две стандартные формы ее представления.
Дизъюнктивно нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входят один раза. Получена ДФН может быть из таблицы истинности по следующему алгоритму:
а) для каждого набора переменных, на котором ФАЛ равна единице, записывают элементарные логические произведения входных переменных, причем переменные равные нулю, записывают с инверсией;
б) логически суммируют все произведения.
Пример: 1.5 Записать ДНФ для ФАЛ из примера 1.4
Решение: Согласно алгоритму из таблицы 1.5 получим:
Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которые аргументы или его инверсия входят один раз.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
а)для каждого набора переменных, на котором ФАЛ равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значение которых равны единице, записывают с инверсией.
б) Полученные суммы логически перемножают.
Пример: 1.6 Записать КНФ для ФАЛ, заданной в примере1.5.
Решение:
