9.1. Деформации в прямых стержнях при растяжении – сжатии.

Математическая модель стержня при растяжении содержит: уравнение равновесия, геометрические соотношения Коши и физические соотношения, выражаемые законом Гука.

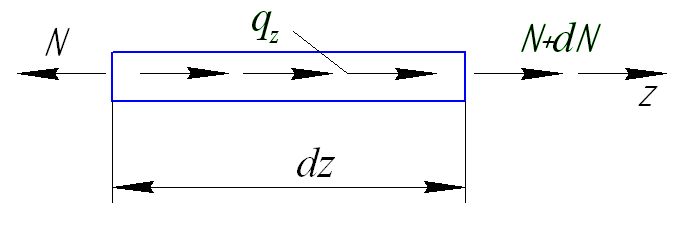
Рисунок 30. Схема нагружения элемента стержня при растяжении.

• Уравнение равновесия элемента стержня в проекциях сил на ось z

(9.1)

, (9.2)

где – продольная сила;

- погонная продольная нагрузка.

• Геометрическое соотношение. Формула Коши. В соответствии с гипотезой плоских сечений перемещение плоского сечения перпендикулярного оси является функцией одной переменной 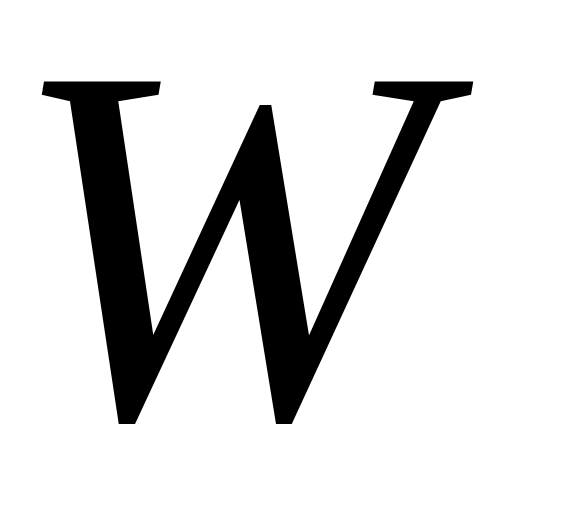(рисунок 31) . Формула Коши устанавливает дифференциальную зависимость между продольными перемещениями стержня 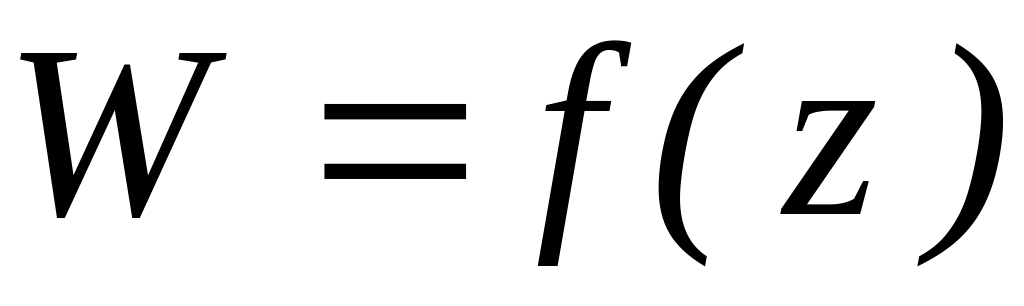и относительной линейной деформацией

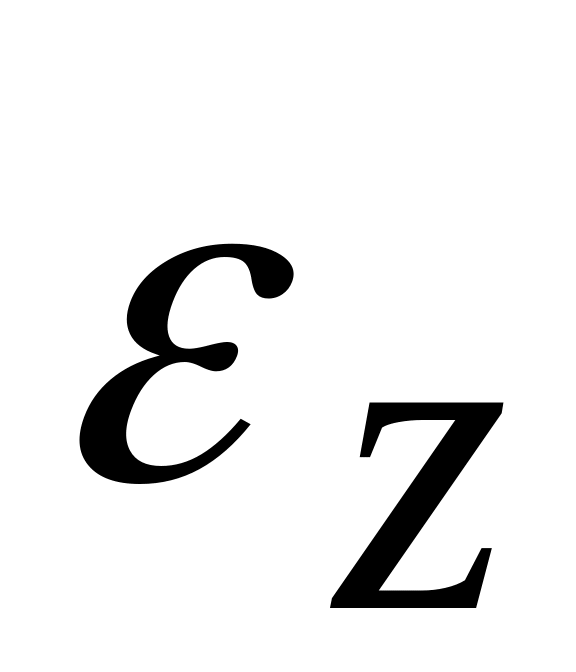
. (9.3)

• Физические зависимости. Закон Гука при одноосном напряженном состоянии

, (9.4)

где - нормальные напряжения в поперечном сечении стержня.

При равномерном распределении напряжений в поперечном сечении получаем продольную силу

, (9.5)

где – площадь поперечного сечения стержня.

После последовательной подстановки в уравнение (9.5) выражений (9.4) и (9.3)

, (9.6)

и с учетом (9.2) получается математическая модель прямого стержня при растяжении - сжатии

(9.7)

Продольные перемещения находятся двукратным интегрированием выражения (9.7)

(9.8)

где нагрузочная функция, зависящая от заданной нагрузки ;

и – постоянные интегрирования определяемые из граничных условий.

Если стержень находится в линейноупругой среде, препятствующей продольным перемещениям прямого стержня и имеющей жесткость , то сопротивление среды будет пропорционально продольным перемещениям и направлено против этих перемещений

(9.9)

а дифференциальное уравнение (9.7) принимает вид

, (9.10)

где .

Такая математическая модель может быть использована для определения продольных перемещений магистрального трубопровода в случае линейной модели грунта. Однако, исследования показали, что она применима только для малых перемещений, а для больших перемещений существует нелинейная зависимость между сопротивлением грунта и продольными перемещениями .

Чтобы повысить точность расчетов на практике применяют нелинейную модель, которая отражает реальные свойства грунта.

9.2. Сопротивление грунта продольным перемещениям трубы.

Для определения зависимостей сопротивления грунта – продольное перемещение, проводят эксперименты и строят диаграммы.

Чтобы оценить сопротивление грунта продольным перемещениям магистрального трубопровода, проводят следующие эксперименты. Сквозь изучаемый грунт перемещают отрезок трубы вдоль его оси и с помощью динамометра определяют силу сопротивления грунта.

Результаты измерений наносят на диаграмму. По оси абсцисс откладывают продольные перемещения отрезка трубы , как недеформируемого тела, по оси ординат – среднее значение cопротивления грунта сдвигу по поверхности трубы .

После того, как диаграмма полностью построена, на ней можно выделить три главных участка:

1 – между перемещением трубы и сопротивлением грунта, почти линейная зависимость. Это первая фаза напряженного состояния грунта – фаза уплотнения, когда грунт уплотняется и приобретает свойства упругого тела;

2 – нарушается пропорциональность между перемещением трубы и сопротивлением грунта, доля упругих деформаций уменьшается, остаточные деформации нарастают;

3 – почти прямая линия параллельная оси абсцисс, которая характеризует равномерное перемещение отрезка трубы. На этом участке грунт находится в стадии предельного равновесия, а между трубой и грунтом устанавливается пластическая связь, которая описывается свойством пластического тела Прандтля-Кулона.

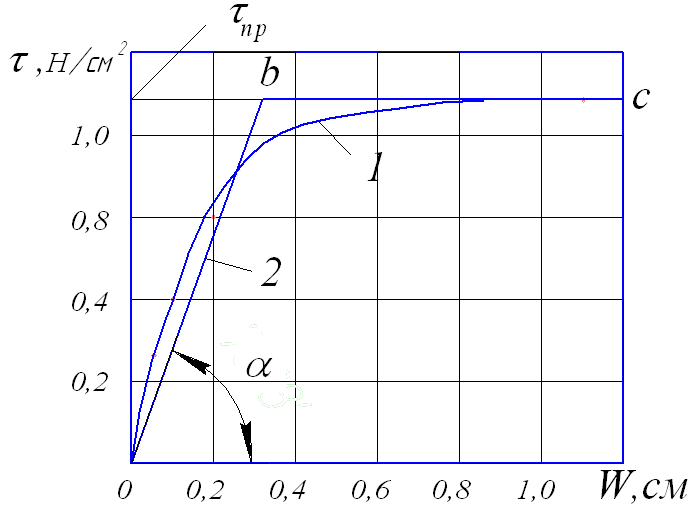
Рисунок 32. Диаграмма сопротивления грунта продольным перемещениям.

1 – диаграмма реального грунта; 2 – билинейная диаграмма.

Для того, чтобы максимально упростить решение полученной математической модели на практике зависимость сопротивления грунта от продольного перемещения линеаризировать, т.е. заменить двумя прямолинейными участками.

На первом участке в области упругих деформаций эта зависимость описывается уравнением прямой

, (9.11)

где – обобщенный коэффициент касательного сопротивления грунта (коэффициент постели грунта при продольных перемещениях); на диаграмме этот коэффициент определяется углом наклона первого участка к оси абсцисс (рисунок 32).

Второй участок параллелен оси абсцисс и определяется уравнением прямой , где - предельное сопротивление грунта.

Для определения обобщенного коэффициента касательного сопротивления грунта при обработке диаграмм используют условие минимума получаемой ошибки. С этой целью ломаную линию (рисунок 32) проводят таким образом, чтобы площади, образованные экспериментальной кривой и ломаной линией были равны.