Рисование фигур с замкнутым контуром

Следующие функции класса CDC позволяют рисовать фигуры с замкнутым контуром, ограничивающие одну или несколько областей поверхности экрана. К таким фигурам относятся прямоугольник, закругленный прямоугольник, эллипс, сегмент, сектор, многоугольник и множество многоугольников.

Прямоугольник задается координатами левого верхнего и правого нижнего углов и для его отображения необходимо вызвать функцию, имеющую такой прототип:

BOOL CDC::Rectangle( int x1, int y1, int x2, int y2 ); BOOL CDC::Rectangle( LPCRECT lpRect );

В качестве параметра можно использовать указатель на объект класса CRect, который подобен структуре RECT:

typedef struct tagRECT { LONG left; LONG top; LONG right; LONG bottom; } RECT;

Например, для получения прямоугольника, верхний левый угол которого находится в точке с координатами (25, 50), а нижний правый угол — в точке (175, 225), необходимо вызвать такую функцию:

pDC->Rectangle (25, 50, 175, 225);

Для отображения закругленного прямоугольника кроме координат левого верхнего и правого нижнего углов необходимо в функцию CDC::RoundRect() передать ширину и высоту прямоугольника, ограничивающего эллипс, используемый для рисования закругленных углов (рис. 11.4). Прототипы функции такие:

BOOL CDC::RoundRect(int x1,int y1,int x2,int y2,int x3,int y3); BOOL CDC::RoundRect( LPCRECT lpRect, POINT point );

В случае использования второго варианта функции в качестве аргументов передают указатель на объект класса CRect , значения ширины и высоты эллипса в виде полей структуры POINT.

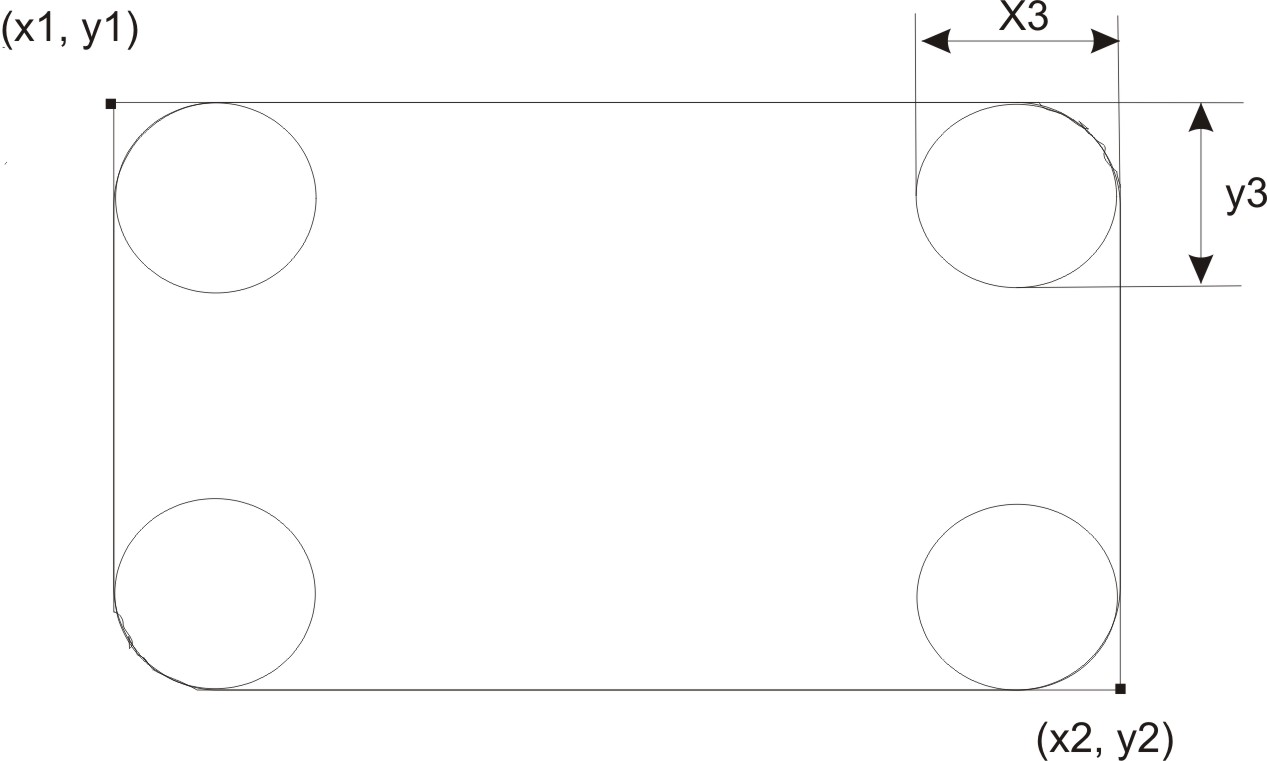
Рис. 11.4. Координаты, переданные в функцию CDC::RoundRect()

Рис. 11.5. Координаты, переданные в функцию CDC::Ellipse()

Эллипсы и окружности отображаются с помощью одной функции, прототипы которой приведены ниже:

BOOL CDC::Ellipse( int x1, int y1, int x2, int y2 ); BOOL CDC::Ellipse( LPCRECT lpRect );

Первая пара координат описывает координаты верхнего левого угла прямоугольника, ограничивающего эллипс, вторая — координаты правого нижнего угла ограничивающего прямоугольника (рис. 11.5). Второй вариант прототипа принимает указатель на объект класса CRect.

Вызвав функцию CDC::Chord(), можно нарисовать сегмент, который образуется пересечением эллипса и хорды. Прототипы функции приведены ниже.

BOOL CDC::Chord( int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4 ); BOOL CDC::Chord( LPCRECT lpRect, POINT ptStart, POINT ptEnd );

Первые две пары координат, передаваемые в функцию CDC::Chord(), описывают прямоугольник, ограничивающий эллипс; третья — начальную точку хорды; четвертая — конечную точку. Как и в функции CDC::Arc(), заданная хордой фигура рисуется из начальной точки в конечную против часовой стрелки, если для изменения направления не вызвана функция CDC::SetArcDirection(), а заданные начальная и конечная точки не лежат на эллипсе (рис. 11.6).

Рис. 11.6. Координаты, переданные в функцию CDC::Chord()

Для вызова функции CDC::Chord(), определенной вторым вариантом прототипа, в качестве аргументов передают указатель на объект класса CRect (ограничивающий прямоугольник), значение полей структуры POINT, определяющих координаты начальной и конечной точек хорды.

Для рисования сектора вызывают функцию CDC::Pie() с прототипом, который определен таким образом:

BOOL CDC::Pie( int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4 ); BOOL CDC::Pie( LPCRECT lpRect, POINT ptStart, POINT ptEnd );

Координаты, передаваемые в функцию CDC::Pie(), аналогичны координатам, передаваемым в функции CDC::Arc() и CDC::Chord() (рис. 11.7).

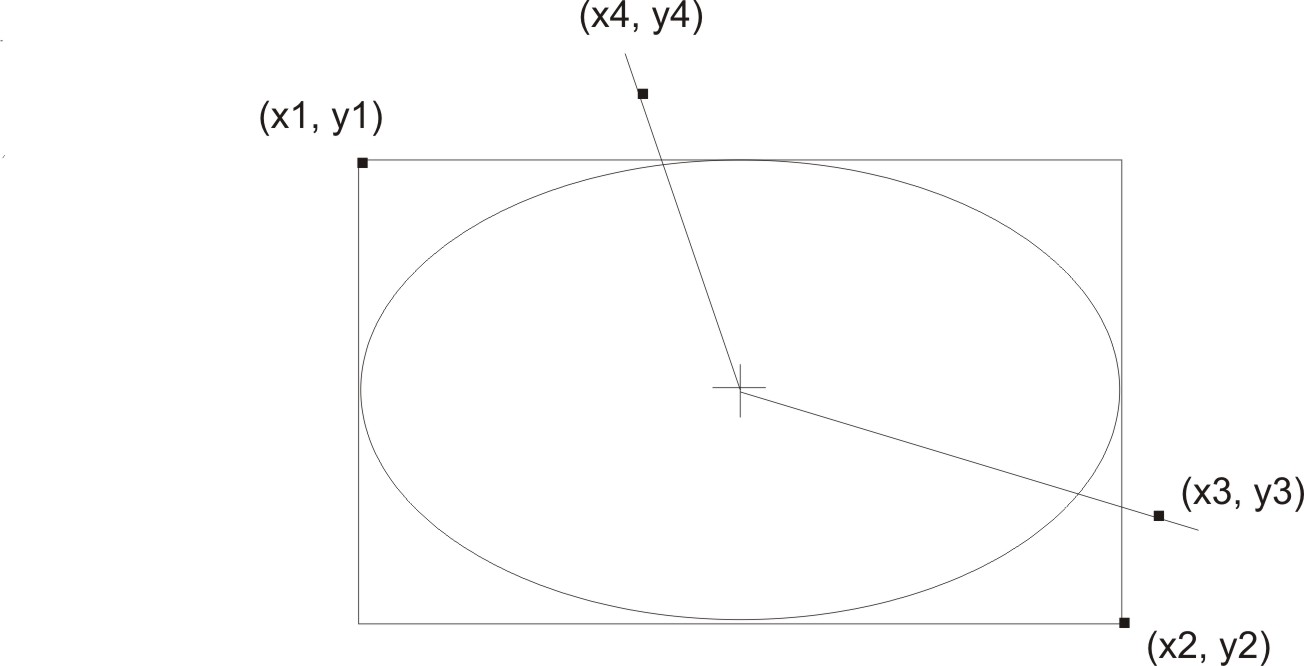
Рис. 11.7. Координаты, переданные в функцию CDC::Pie()

Функция CDC::Polygon() рисует многоугольник, состоящий из двух или более вершин, соединенных линиями. Многоугольник требует указания координат каждой его вершины и количество вершин, которые необходимо соединить. Функция принимает в качестве аргументов указатель на массив точек, которые определяют координаты вершин многоугольника. Каждая точка массива является структурой POINT или объектом класса CPoint. В классе CDC функция объявлена таким образом:

BOOL CDC::Polygon( LPPOINT lpPoints, int nCount );

Например, следующие строки рисуют треугольник

POINT lpPoints [3]; lpPoints [0].x = 20; lpPoints [0].y = 10; lpPoints [1].x = 30; lpPoints [1].y = 30; lpPoints [2].x = 10; lpPoints [2].y = 30; pDC->Polygon (lpPoints, 3);

В отличие от функции CDC::Polyline(), рассмотренной выше, функция CDC::Polygon() всегда создает замкнутую фигуру (кроме случая, когда соединяемых вершин всего две). Чтобы фигура имела замкнутый контур, при необходимости проводится линия из последней вершины в первую. В приведенном примере функция CDC::Polygon() соединяет первую точку (lpPoints [0]) со второй, вторую с третьей и третью с первой, образуя треугольник. Если этот массив точек передать функции CDC::Polyline(), то она соединит первую точку со второй, а вторую точку с третьей.

В одном вызове функции CDC::PolyPolygon() можно нарисовать несколько отдельных многоугольников. Можно вызвать функцию CDC::PolyPolygon(), чтобы изменить режим заполнения многоугольника. Прототип функции такой:

BOOL PolyPolygon( LPPOINT lpPoints, LPINT lpPolyCounts, int nCount );

Параметрами функции являются lpPoints — указатель на массив структур типа POINT или объектов класса CPoint, которые определяют координаты вершин многоугольников; lpPolyCounts — указатель на массив целых чисел, каждое из которых определяет количество вершин в одном многоугольнике; nCount — количество многоугольников.

Для каждой из замкнутых фигур, рассмотренных в этом параграфе, границы рисуются с помощью текущего пера, а внутренние области заполняются текущей кистью. Обратите внимание: при рисовании замкнутой фигуры пером, которому присвоен стиль PS_INSIDEFRAME, граница рисуется внутри ограничивающего прямоугольника. Если нужно нарисовать замкнутую фигуру без закрашивания (т.е. оставить внутреннюю область без изменений), то вызывается функция CDC::SelectStockObject(), позволяющая выбрать объект NULL_BRUSH перед рисованием.

Класс CDC инкапсулирует более 170 функций, из них функций рисования более 40. Мы рассмотрели только некоторые их них. В табл. 11.1 приведены некоторые дополнительные функции рисования, инкапсулированные в классе CDC.

Т а б л и ц а 11.1