- •Методология исследований при моделировании свойств и качественных характеристик изделия
- •1.1 Словарь основных понятий и определений системного анализа
- •Алгоритм системного анализа технического объекта (изделия)
- •1.4 Суждение как форма экспертного заключения.
- •1.4 Метод расчета точности функционального свойства при анализе технического устройства
- •2 Химические и физические связи реальных тел
- •2.1 Общие сведения о химических связях.
- •2.2 Физико-химические модели структурообразования при кристаллизации и коагуляции синтетических систем.
- •3.1 Отклик на внешнее механическое воздействие
- •1.8 Классификация по физико-механическим и технологическим свойствам
- •4. Деформация реальных твердых тел
- •Общие сведения о твёрдых телах.
- •5. Напряжение и деформация
- •5.1 Теория упругих напряжений
- •5.2 Чистый сдвиг (упругие деформации)
- •5.3 Теория пластичных деформаций
- •4. Упругие материалы
- •4.1. Введение. Определения
- •4.2. Линейные упругие (гуковские) материалы
5. Напряжение и деформация
5.1 Теория упругих напряжений
Одноосное нормальное напряжение. Под влиянием внешних сил в упругих телах возникают деформации, которые зависят от распределения силы. Физические основания для изучения деформации принимаются из экспериментальных данных опытом на растяжение и сжатие.
|
|
|
|
Прямой
цилиндрический стержень длиною ℓ0
и диаметром d0
нагружен на своих конечных плоскостях
двумя равными, противоположно
направленными, равномерно распределенными
по этим плоскостям силами. В поперечных
сечениях на площади сечения А растягивающая
сила распределяется равномерно; таким
образом возникает растягивающее
напряжение σ = Р/А в направлении оси
стержня. Одновременно начальная длина
ℓ0
возрастает до длины ℓ. Изменение длины
цилиндрического стержня будет равно
![]() ℓ
= ℓ - ℓ0
(абсолютное удлинение). Его отношение
к начальной длине ε = ℓ/ℓ0
называется относительным удлинением.
ℓ
= ℓ - ℓ0
(абсолютное удлинение). Его отношение
к начальной длине ε = ℓ/ℓ0
называется относительным удлинением.
На рис ( ) представлена диаграмма удлинений и напряжений для общего случая нагрузки. Растягивающее напряжение σ нанесено как функция удлинений ε. Так как поперечное сечение изменяется, то для определения напряжений принимают начальную площадь А0; σ = Р/А0. Линия ОРSBZ есть линия напряжений. Сначала напряжение растет вместе с удлинением. Для многих материалов обе величины пропорциональны до границы пропорциональности Р; тогда ОР линия прямая. На границе удлинений или текучести S напряжение достигает значения σS; здесь начинается течение – удлинение без повышения напряжения (условного).
Напряжение
при этом падает несколько от ![]() (верхняя граница течения) до
(верхняя граница течения) до ![]() (нижняя граница течения). По окончании
течения напряжение поднимается дальше
и достигает у точки В1
наивысшего значения σВ
– временного сопротивления (прочность
при растяжении). Поперечное сечение
стержня значительно уменьшается здесь
(образование шейки); при дальнейшем
растяжении испытывают удлинение только
части стержня вблизи шейки. Напряжения,
отнесенные к основному сечению, падают
– и у точки Z
стержень разрушается.
(нижняя граница течения). По окончании
течения напряжение поднимается дальше
и достигает у точки В1
наивысшего значения σВ
– временного сопротивления (прочность
при растяжении). Поперечное сечение
стержня значительно уменьшается здесь
(образование шейки); при дальнейшем
растяжении испытывают удлинение только
части стержня вблизи шейки. Напряжения,
отнесенные к основному сечению, падают
– и у точки Z
стержень разрушается.
Если удлиненный на определенную величину стержень разгружается, то деформация исчезает не полностью. Именно удлинение распадается на исчезающую упругую часть ℓ1 и остающееся удлинение ℓ2. При малых нагрузках остающееся удлинение очень незначительно по сравнению с упругим. Напряжение σℓ, до которого остающееся удлинение незначительно, называется пределом упругости.
По постановлению Международного конгресса по испытанию материалов в 1906 г. предел пропорциональности есть напряжение, при котором остающаяся деформация достигает значения 1:100%.
Упругость и эластичность. При научных исследованиях нередко бывает, что обнаруживается сходство между далекими друг от друга явлениями. Сначала оно непонятно и потому кажется случайным. Затем выясняется, что в основе сходства явлений лежит некий фундаментальный принцип или закон природы.
Когда растягивается резиновая лента или слабая металлическая пружина, ощущения отклика на внешнее воздействие очень похожи.
Упругость большинства твердых (кристаллических) тел, в том числе и металлов, имеет совершенно иной характер, чем у полимеров. Растягивающее усилие увеличивает в них средние межатомные расстояния. При снятии нагрузки силы притяжения возвращают атомы в исходное состояние (положение). По закону Гука, закон пропорционального удлинения тела Δl под действием приложенного усилия σ и обратно пропорциональна его модулем упругости E, имеет соотношения:
|
|
Где
![]() – первоначальная длина тела;
– первоначальная длина тела;
σ = f/A – усилие на единицу поверхности сечения (напряжение);
E - модуль упругости первого рода.
Силы
взаимодействия между атомами очень
велики. Поэтому модули упругой деформации
имеют огромную величину. Например, для
стали Е = 20 000 кг/мм2,
для стекла Е = 5000 кг/мм2,
для мягких металлов (олово, свинец Е =
2000…3000 кг/мм2. Это означает, что даже для
небольшой деформации ![]() к наиболее мягким металлам нужно
приложить усилие σ = 200…300 Н/мм2. Для
обратимой деформации, после которой
материал еще восстанавливает первоначальную
форму, значения удлинения и вовсе малы
– несколько десятых или даже сотых
долей процента.
к наиболее мягким металлам нужно
приложить усилие σ = 200…300 Н/мм2. Для
обратимой деформации, после которой
материал еще восстанавливает первоначальную
форму, значения удлинения и вовсе малы
– несколько десятых или даже сотых
долей процента.
Как не похожи на это свойства резины. Модуль упругости резины Е = 1 Н/мм2, а обратимые деформации 500% и более. Подобные свойства и у других полимеров в высокоэластическом состоянии. Многие полимеры (пластики, органические стекла) при нормальных условиях среды пластичны, но стеклоподобны – они не способны к большим обратимым деформациям. При повышении температуры полимерные пластики переходят в высокоэластическое состояние, становятся каучукоподобными.
Но различие в упругости между металлами и полимерами при изменении температуры идет еще дальше. Модули упругости металлов и вообще кристаллических тел уменьшаются с ростом температуры. Нагревание облегчает их деформацию. На этом свойстве основана горячая обработка металлов: кузнец разогревает заготовку в печи до красна.
А вот модуль упругости полимеров, наоборот, возрастает с ростом температуры. Полимер при нагревании становится менее податливым. Такое странное свойство из всех твердых тел присуще только полимерам.
Например. К толстой полоске растянутой резины прикрепить динамометр, нагревать окружающую среду (электроплиткой). Показания динамометра начнут увеличиваться – напряжение возросло.
Аналогия поведения упругости – твердый полимер и газ.
Проявление упругости газа можно наблюдать при его нагревании. Возьмем грамм-молекулу идеального газа. Уравнение его состояния PV=RT утверждает, что если температура не меняется, произведение давления газа на его объем также постоянно. Проведем мысленно несложный опыт, предложенный В.Э Эскиным [ ]. Пусть газ в вертикальном цилиндре (высота Н. площадь сечения s), закрытом легким поршнем (рис. ). Кладем на поршень груз F, после чего он опустится на отрезок ΔН, слегка сжав газ до давления (Р + F/s). Считая, что температура газа не изменилась, можно написать уравнение состояния газа:
или
|
|
Отношение
F/s
есть сжимающее усилие (напряжение - σ)
в сечении деформируемого тела – газа,
а т.к. ΔН![]() Н
– изменение высоты объема, то отношение
слева напоминает отношение
Н
– изменение высоты объема, то отношение
слева напоминает отношение ![]() .
Сравнив уравнение состояния газа с
законом Гука, видим, что при сжатии газа
роль модуля упругости играет давление
газа Р.
.
Сравнив уравнение состояния газа с
законом Гука, видим, что при сжатии газа
роль модуля упругости играет давление
газа Р.
Это
примечательно в двух отношениях.
Во-первых, Р = 1 ат = 0,01 кг/мм2,
значит модуль сжатия газа близок к
модулю упругости резины (![]() 0,1 кг/мм2).
Во-вторых. Давление газа (при постоянном
объеме) пропорционально температуре.
А это означает, что модуль упругости
газа так же, как и резины, растет с ростом
температуры. Чем выше температура. Тем
больше средняя скорость молекул, а
значит, их импульс при ударе о поршень.
Аналогичная ситуация при растягивании
резины. Растягивая макромолекулы, нужно
преодолевать тепловое движение звеньев,
которое свертывает цепи в клубки. Чем
выше температура, тем интенсивнее
движутся части молекулы (звенья,
сегменты), тем большая требуется сила,
чтобы преодолевать противодействие
растяжению. Сходство упругих свойств
полимеров и газов основано на общности
природы их упругости.
0,1 кг/мм2).
Во-вторых. Давление газа (при постоянном
объеме) пропорционально температуре.
А это означает, что модуль упругости
газа так же, как и резины, растет с ростом
температуры. Чем выше температура. Тем
больше средняя скорость молекул, а
значит, их импульс при ударе о поршень.
Аналогичная ситуация при растягивании
резины. Растягивая макромолекулы, нужно
преодолевать тепловое движение звеньев,
которое свертывает цепи в клубки. Чем
выше температура, тем интенсивнее
движутся части молекулы (звенья,
сегменты), тем большая требуется сила,
чтобы преодолевать противодействие
растяжению. Сходство упругих свойств
полимеров и газов основано на общности
природы их упругости.
Растяжение цепных молекул переводит их в менее вероятную конфигурацию. Сжатому газу также отвечает менее вероятное состояние. Увеличение объема газа всегда связано с возрастанием беспорядка, с большими возможностями размещения молекул. В увеличенном объеме то же самое число молекул можно расположить возросшим числом способов, а это и значит, что вероятность состояния возросла.
Вероятность состояния измеряют в физике особой величиной, называемой энтропией (S). Формула для вычисления энтропии системы (тела) в некотором состоянии
|
|
где С – число способов, которыми данное состояние осуществляется;
k – постоянная Больцмана.
Согласно формуле энтропия растет вместе с С, значит, когда система переходит в состояние с большей вероятностью – это сопровождается возрастанием энтропии
|
|
где V1 и V2 - объем газа до и после расширения.
Так
как ![]() - энтропия газа при расширении
увеличивается.
- энтропия газа при расширении
увеличивается.
Упругость тел, связанную с вероятностью состояния, принято называть энтропийной упругостью.
Материал тем эластичнее, чем больше упругое удлинение ℓ1 по сравнению с общим удлинением ℓ. Отношение ℓ1:ℓ служит мерой упругого совершенства (при определенной нагрузке). Для вполне упругого тела
ℓ1 : ℓ = 1 |
|
После перехода предела упругости пластическая часть деформации возрастает все более. После границы текучести деформация становится пластической (пластическая область). У многих материалов отсутствует граница текучести и чистая упругая область постепенно переходит в чисто пластическую. Вязкие материалы – это материалы с пластической областью. Хрупкие материалы или совсем не имеют (вязкости) пластической деформации, или последняя очень мала.
Деформация, в зависимости от материала, требует большего или меньшего времени для своего развития: это – явление так называемого упругого последействия. Деформация и также прочность зависят от времени, в течение которого нагрузка возрастает от нуля до наибольшего значения и зависит от продолжительности действия каждой нагрузки. Особенно сильное упругое последействие обнаруживают железо и цинк.
Деформация и различные пределы (пропорциональности, упругости, временного сопротивления и т.п.) зависят от температуры.
Соответственное
явление происходит при сжатии: вместо
предела текучести имеется предел
расплющивания (предел текучести при
сжатии) с направлением ![]() ,
при котором материал без повышения
напряжения течет в различные стороны.
Разрушение происходит при сопротивлении
раздроблению (прочность на сжатие,
временное сопротивление на сжатие)
,
при котором материал без повышения
напряжения течет в различные стороны.
Разрушение происходит при сопротивлении
раздроблению (прочность на сжатие,
временное сопротивление на сжатие) ![]() .
.
При
повторно переменной нагрузке разрушение
наступает при значительно меньшем
напряжении: прочность при колебательной
нагрузке или предел выносливости ![]() есть то наибольшее напряжение, которое
выдерживает материал при колебательной
нагрузке (знакопеременное сжатие и
растяжение – напряжение с переходом
через нуль). Произвольно большое число
раз. Практический предел выносливости
для известного числа циклов изменения
нагрузки (10∙106,
20∙106
и
т.д.) называется пределом усталости.
Предел прочности при переменной нагрузке
есть то наибольшее напряжение, которое
выдерживает материал при колебательной
нагрузке (знакопеременное сжатие и
растяжение – напряжение с переходом
через нуль). Произвольно большое число
раз. Практический предел выносливости
для известного числа циклов изменения
нагрузки (10∙106,
20∙106
и
т.д.) называется пределом усталости.
Предел прочности при переменной нагрузке
![]() есть то наибольшее напряжение, которое
материал выдерживает произвольное
число раз при изменении его значений
от нуля в одну сторону.
есть то наибольшее напряжение, которое
материал выдерживает произвольное
число раз при изменении его значений
от нуля в одну сторону.
Прочность при колебательной нагрузке значительно меньше, чем прочность при переменной нагрузке. У вязких металлов предел выносливости и предел прочности при переменной нагрузке лежат ниже предела текучести.
В
теории упругих деформациях рассматриваются
только те явления, в которых граница
текучести не достигнута (рис ) участок
кривой от точки О до точки ![]() .
.
|
|
|
Рис Диаграмма напряженного состояния в координатах напряжения от деформации |
||
Кроме того, при расчетах принимается, что материал изотропен, т.е. что состояние (упругое и пластическое) по всем направлениям одинаково. Если призматическое тело нагружается в одном направлении центральной силой, которая распределяется равномерно по сечению, то имеем случай одноосного нормального напряжения.
Пусть
осевая сила равна Р, положительная –
растягивающая сила, отрицательная –
сжимающая сила. Нормальное напряжение
в осевом направлении определится σ =
Р/А, где А – площадь поперечного сечения
(плоскость сечения перпендикулярна
действию силы), положительный знак
относится к напряжению растяжения,
отрицательный к напряжению сжатия.
Длина ℓ0
изменяется при этом до ℓ. Абсолютное
удлинение
ℓ
= ℓ
-
ℓ0
положительное при растяжении, отрицательное
при сжатии. Относительное удлинение
равно ![]() . При сжатии относительное удлинение
отрицательно; абсолютное изменение
будет укорочение. Также меняются размеры
поперечного сечения: при удлинении,
происходит уменьшение их, при сжатии
увеличение. Сторона сечения
. При сжатии относительное удлинение
отрицательно; абсолютное изменение
будет укорочение. Также меняются размеры
поперечного сечения: при удлинении,
происходит уменьшение их, при сжатии
увеличение. Сторона сечения ![]() переходит в
переходит в ![]() .
Абсолютное поперечное сжатие – удлинение
.
Абсолютное поперечное сжатие – удлинение
|
|
относительное поперечное сжатие равно
|
|
При удлинении относительное поперечное сжатие отрицательно, абсолютное сжатие есть уменьшение поперечного размера. Относительное поперечное сжатие (расширение в случае сжатия) есть некоторая дробь осевого удлинения (при сжатии – укорочения):
|
|
|
|
![]() - коэффициент поперечного сжатия
(коэффициент Пуассона).
- коэффициент поперечного сжатия
(коэффициент Пуассона).
При
отсутствии поперечного сжатия
= 0; для материалов, у которых объем при
сжатии и растяжении не изменяется, ![]() .
Действительные значения коэффициентов
поперечного сжатия лежат между этими
пределами: для металлов принимается
.
Действительные значения коэффициентов
поперечного сжатия лежат между этими
пределами: для металлов принимается
![]()
Данные опыта. Для железа значение 1/μ лежит между 3,3 и 3,5. По Планку 1/μ убывает с температурой (для железа очень медленно) и приближается при температуре плавления к нижнему пределу, равному 2,0, который относится к жидкости σmax = 63 Мпа.
Для того чтобы притти к простым решениям, в сопротивлении материалов обыкновенно принимают, что напряжение пропорционально удлинению. Этот закон пропорциональности (закон Гука) имеет значение в определенных границах для всех важнейших материалов:
σ
= или
ɑ·σ
= где Е – модуль упругости, постоянная характеристика металла МПа.;
= |
|
Найденные на основании этого допущения формулы относятся также к тем материалам, для которых закон пропорциональности не исполняется строго.
Если
между напряжением и деформацией нет
никакой пропорциональности, то Еσ
= ![]() , т.е.
Еσ
есть
производная функция удлинений и
напряжений.
, т.е.
Еσ
есть
производная функция удлинений и
напряжений.
Работа деформации для определенного удлинения равна
|
|
внутри границ пропорциональности
|
|
Работоспособность материалов до разрыва (в единице объема) может быть выражена по площади под кривой на диаграмме деформация - напряжение. Необходимо точное определение масштабных коэффициентов осей диаграммы.
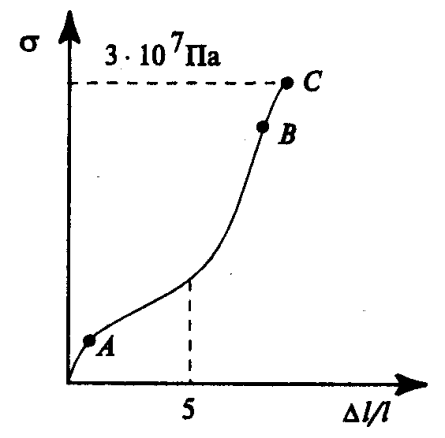
В состоянии растяжения материалов со специфическими свойствами упругости (сталь – это упругий поликристаллический материал) и высокоэластичности (резина – это эластичный полимерный материал) наблюдается большое различие. На рис. ( ) представлены характерные поведения свойств упругости и высокоэластичности в координатах напряжения от деформации.
|
|
Рис. Диаграмма растяжения в координатах напряжения от деформации для стали (левая – упругий материал) и для резины (правая – высокоэластичный материал). Точка А – верхний предел линейного участка зависимости напряжения от деформации; точка В – верхний предел обратимых деформаций; точка С – точка разрыва. |
|
Сравнивая обе кривые по свойствам можно иметь представления о свойствах:
Величины упругой относительной деформации ( ) для резины намного выше, чем для стали (для резины
 , для стали
, для стали  0,01).
0,01).Напряжения σ для стали существенно больше, чем для резины (
 для стали и
для стали и  для каучука).
для каучука).Характерная величина - модуль Юнга (это линия, определяющая начальный наклон кривой зависимости напряжения от деформации),
 Па,
Па,
 что
гораздо больше для стали, чем для каучука
(резины).
что
гораздо больше для стали, чем для каучука
(резины).Для стали, линейность и обратимость теряются почти одновременно, а для резины существует очень широкая область нелинейных обратимых деформаций.
Для стали существует широкая область пластических деформаций (между точками В и С) , которая практически отсутствует для резины.