
3.4. Парабола
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой d. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p>0).
Каноническое уравнение параболы с вершиной в начале координат и осью симметрии Ох имеет вид:
|
(28) |
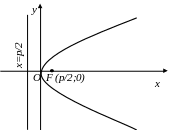
Рис.12.
П
При р<0 ветви параболы в отрицательном направлении оси Ох.
Фокус
лежит на оси симметрии параболы,
проходящей через вершину–оси
,
на расстоянии
![]() от вершины вправо при p>0,
влево при
р<0.
от вершины вправо при p>0,
влево при
р<0.
Директриса
перпендикулярна оси Ох,
проходит
через точку, симметричную фокусу,
относительно вершины, ее уравнение
![]() .
.
Каноническое уравнение параболы с вершиной в начале координат и осью симметрии Оу имеет вид:
|
(29) |
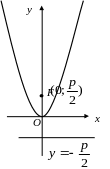
Рис.13.
Здесь
так же при p>0
ветви параболы в положительном направлении
оси Оу. При
P<0
ветви параболы
в отрицательном направлении оси Оу,
координаты
фокуса
![]() ;
уравнение директрисы
;
уравнение директрисы
![]() .
.
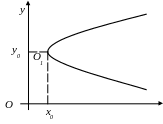
Уравнение параболы с центром в произвольной точке О1(х0;у0) и
осью симметрии у=у0 имеет вид:
|
(30) |
x
Рис.14.
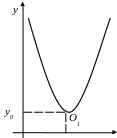
Уравнение параболы с центром в произвольной точке О1(х0;у0) и осью симметрии х=х0 имеет вид:
|
(31) |
O
x
x0
Рис.15.
Чтобы построить параболу по уравнениям (30)-(31) следует сначала выполнить преобразование координат (24), и строить вершину, фокус, ось симметрии и директрису в штрихованных координатах, как по уравнениям (28)-(29).
3.5. Общее уравнение линии второго порядка
Рассмотрим общее уравнение второго порядка относительно текущих координат
|
(32) |
Пусть
![]() ,
если это не так, то поворотом осей
координат по формулам (8), этого можно
добиться. Величина коэффициента на тип
кривой влияния не оказывает, поэтому
его можно не рассматривать.
,
если это не так, то поворотом осей
координат по формулам (8), этого можно
добиться. Величина коэффициента на тип
кривой влияния не оказывает, поэтому
его можно не рассматривать.
Выделим полные квадраты переменных
![]()
Обозначим
![]()
Тогда уравнение (32) примет вид
|
(33) |
который удобен для анализа.
Если
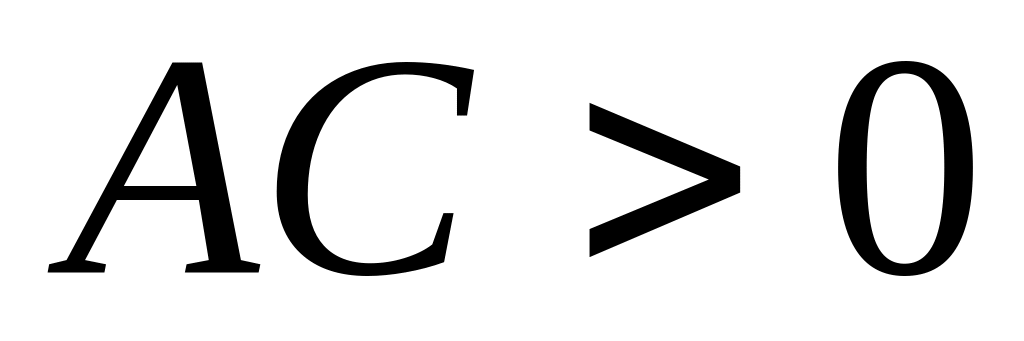 ,
то уравнение (33) является уравнением
эллиптического типа:
,
то уравнение (33) является уравнением
эллиптического типа:
при
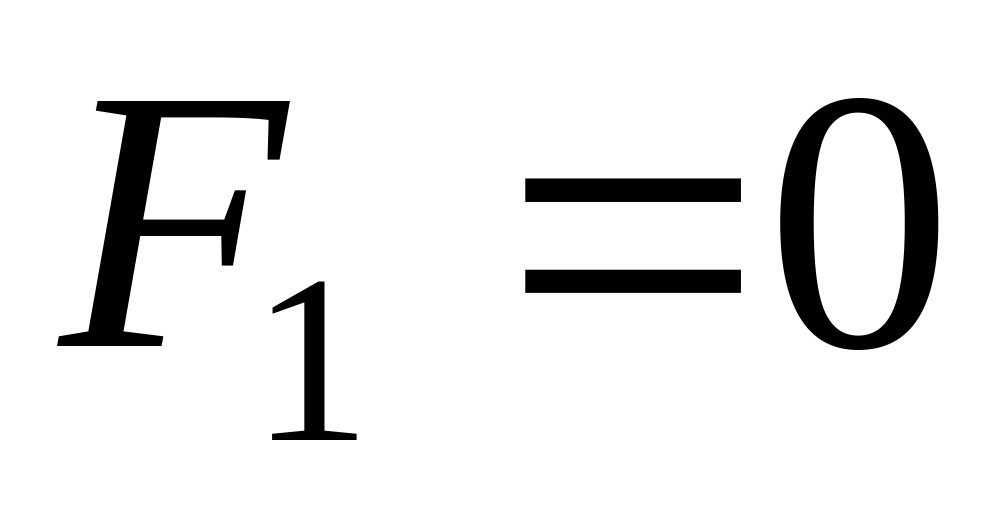 уравнение
уравнение
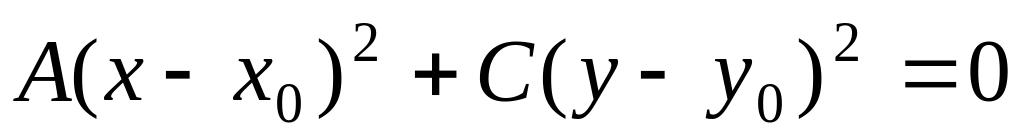 задает точку плоскости с координатами
задает точку плоскости с координатами
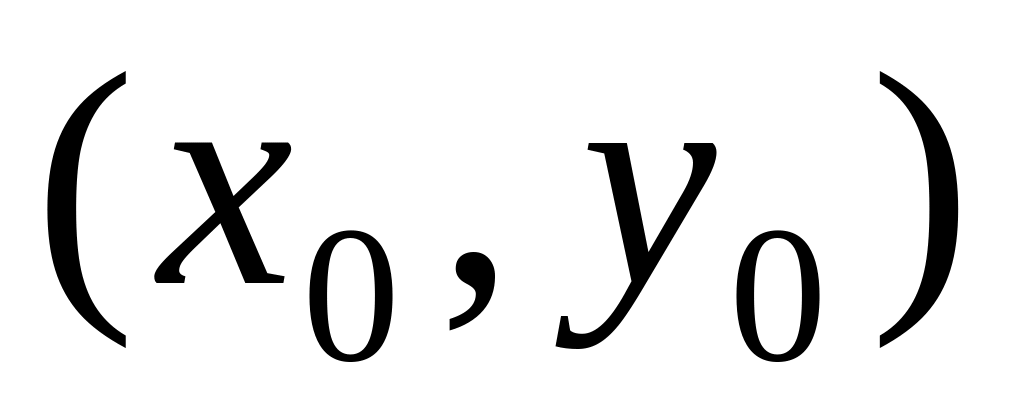 ;
;
при
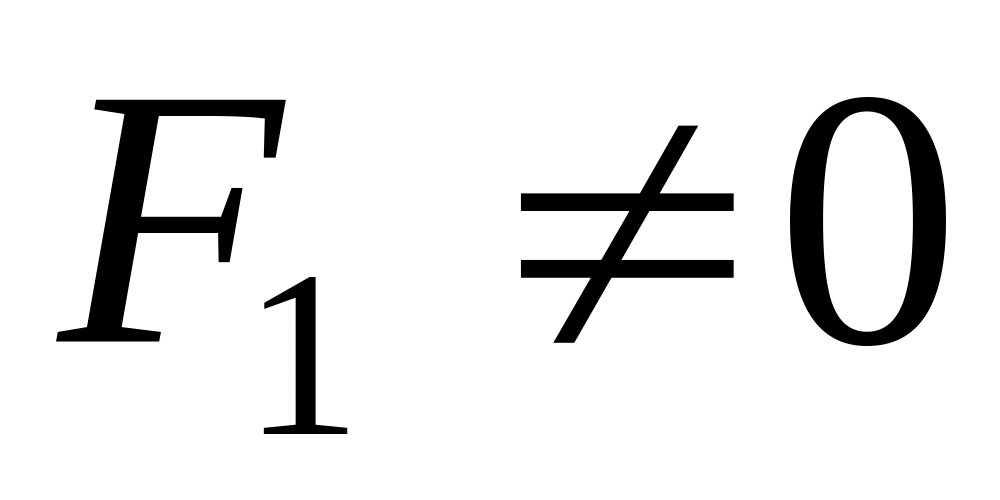 уравнение
уравнение
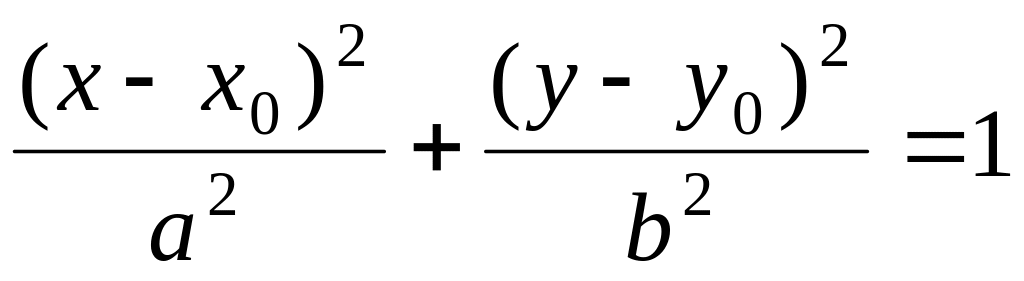 – где
– где
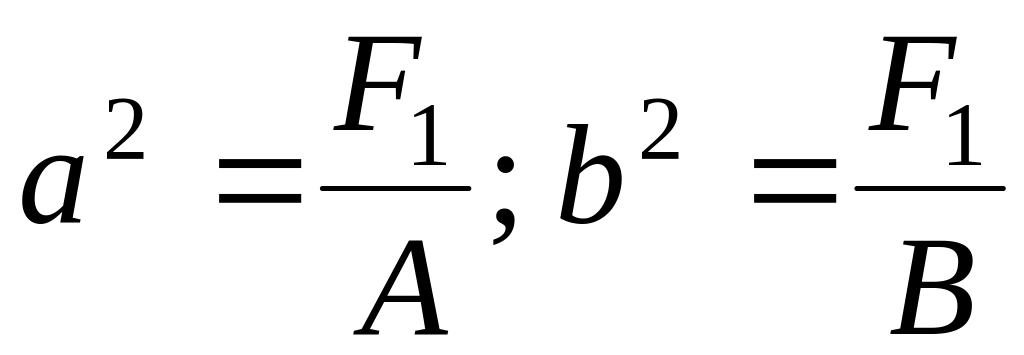 ,
при
,
при
 задает эллипс (см.23); при
задает эллипс (см.23); при
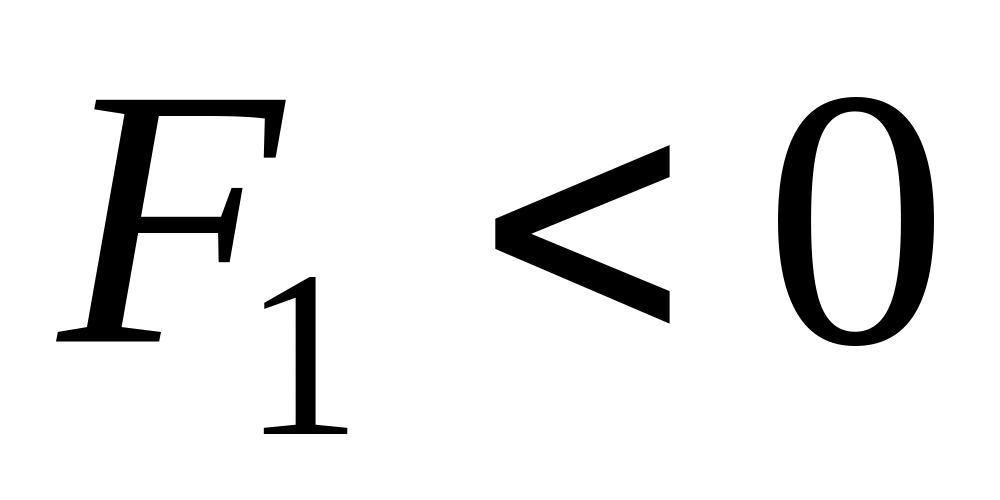 –
мнимый эллипс.
–
мнимый эллипс.
Если
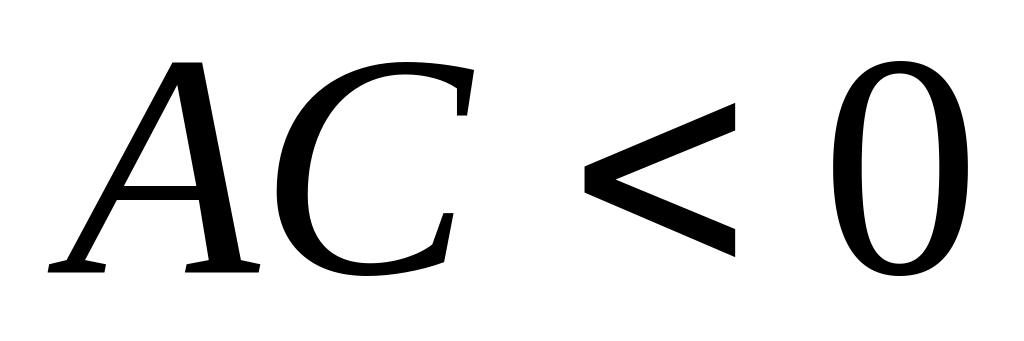 ,
то уравнение (33) является уравнением
гиперболического
типа:
,
то уравнение (33) является уравнением
гиперболического
типа:
при
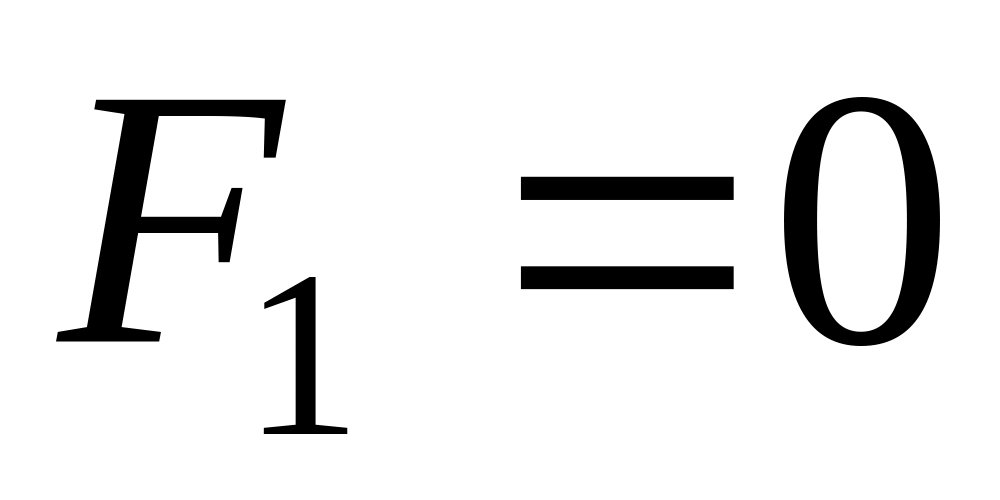 уравнение
уравнение
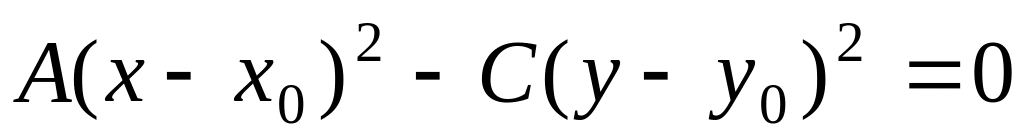 задает пару пересекающихся в точке
прямых;
задает пару пересекающихся в точке
прямых;
при
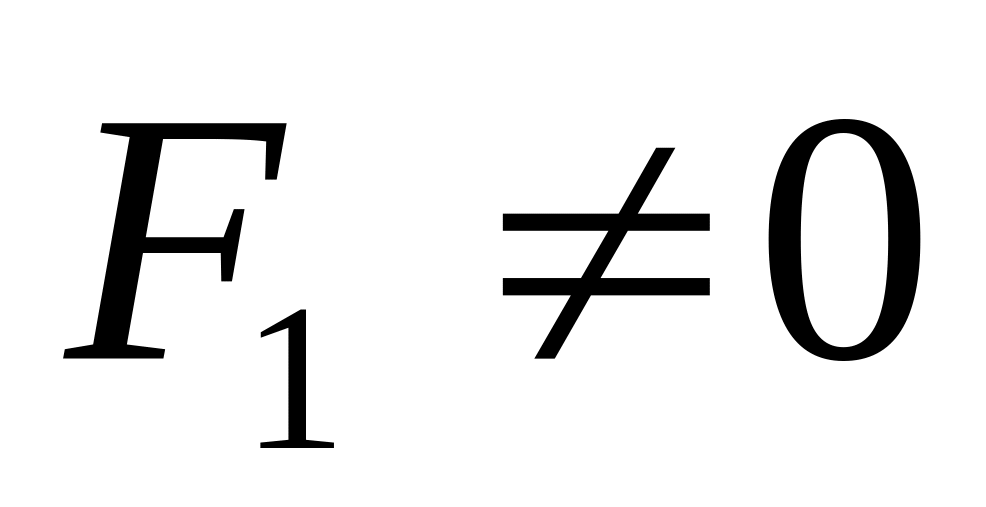 уравнение
уравнение
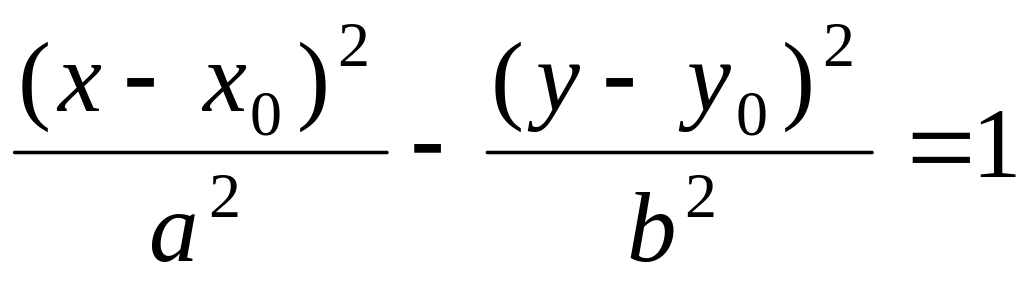 или
или
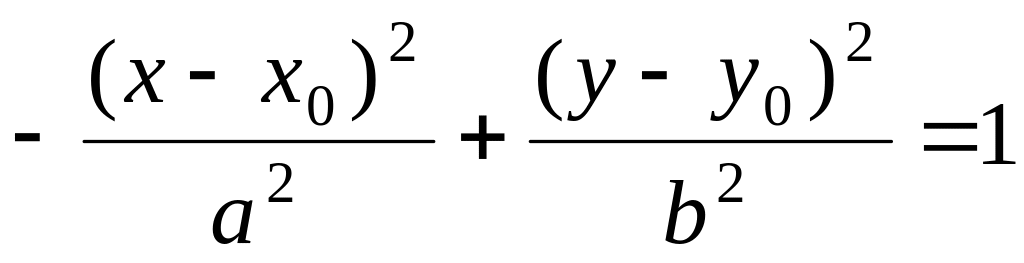 задают гиперболу (27).
задают гиперболу (27).
Если
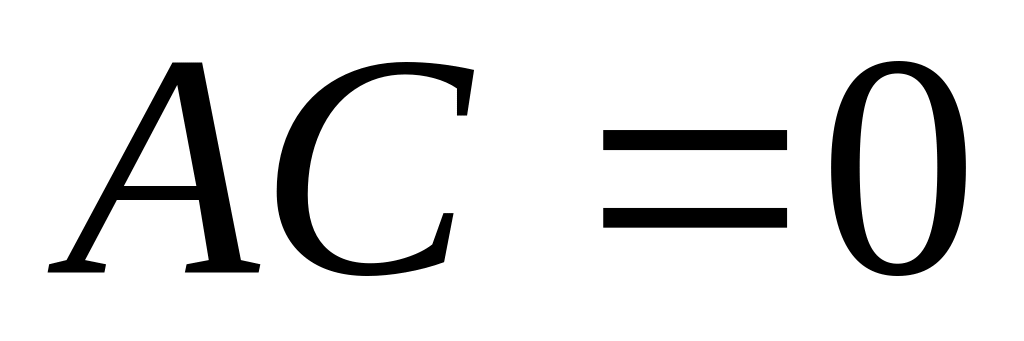 ,
то уравнение (33) является уравнением
параболического
типа:
,
то уравнение (33) является уравнением
параболического
типа:
если
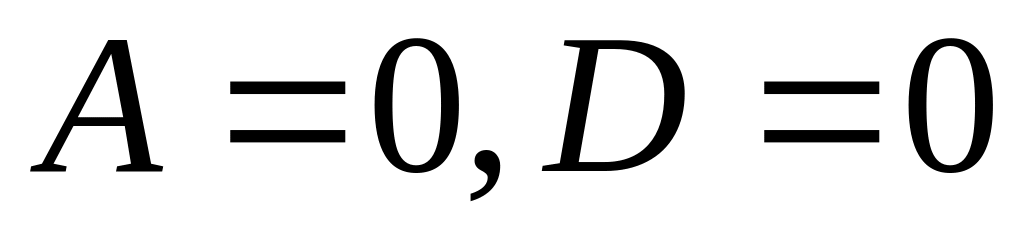 ,то
уравнение
,то
уравнение
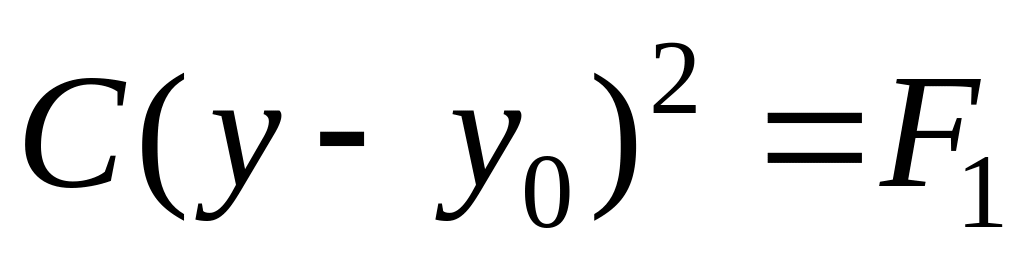 задает пару параллельных оси
прямых;
задает пару параллельных оси
прямых;
если
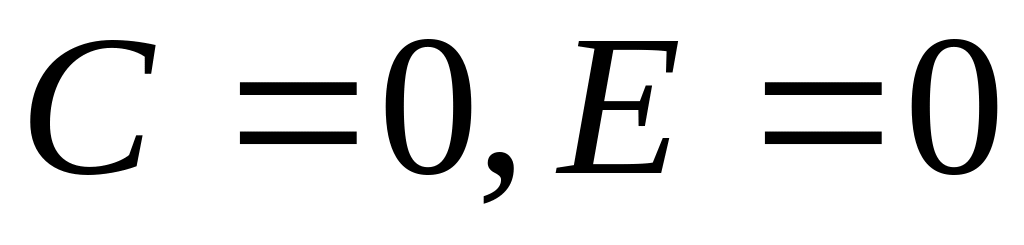 ,
то уравнение
,
то уравнение
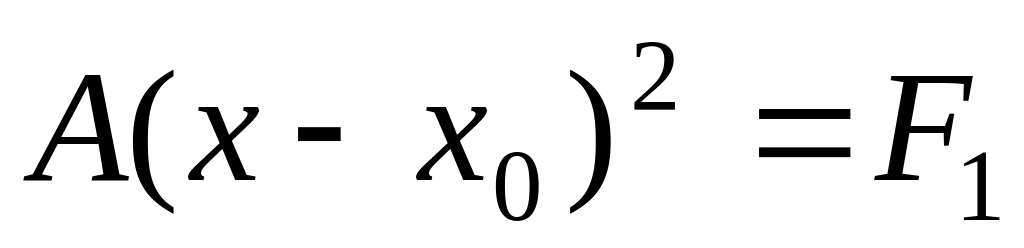 задает пару параллельных оси
прямых;
задает пару параллельных оси
прямых;
в случае если и коэффициент , то прямые сливаются;
если
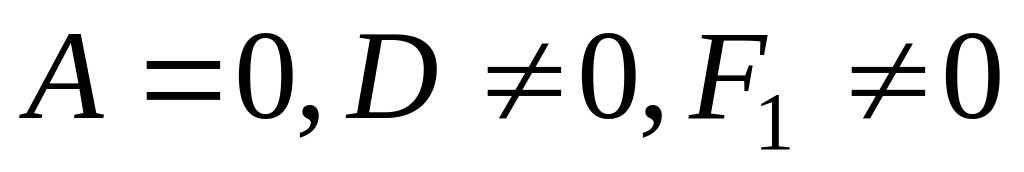 ,то
уравнение (33) преобразуем к
,то
уравнение (33) преобразуем к
![]() ,
тогда уравнение
,
тогда уравнение
![]() ,
,
где
![]() ,
,
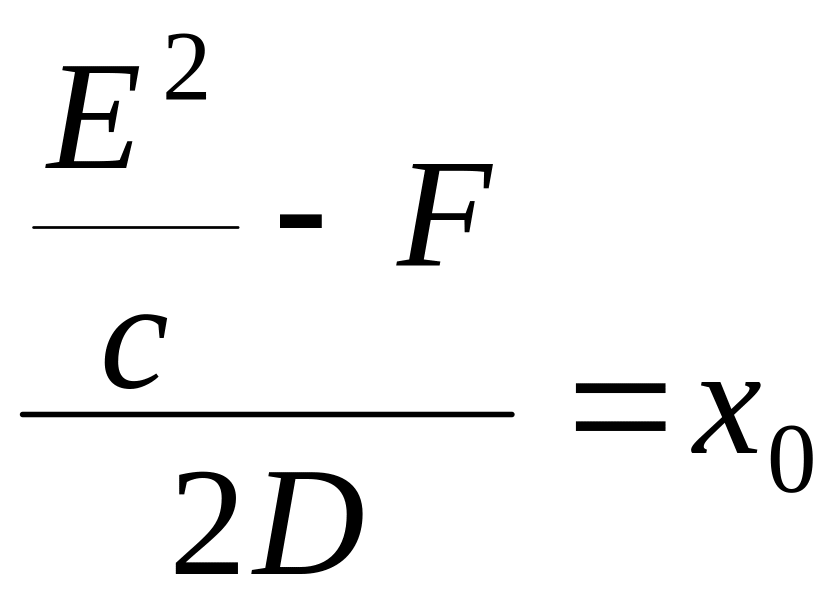 есть уравнение параболы (30).
есть уравнение параболы (30).
если
 ,
то получим уравнение гиперболы (31).
,
то получим уравнение гиперболы (31).
Пример 6. Определить, какая кривая задана уравнением, найти основные параметры и построить:
![]()
Решение:
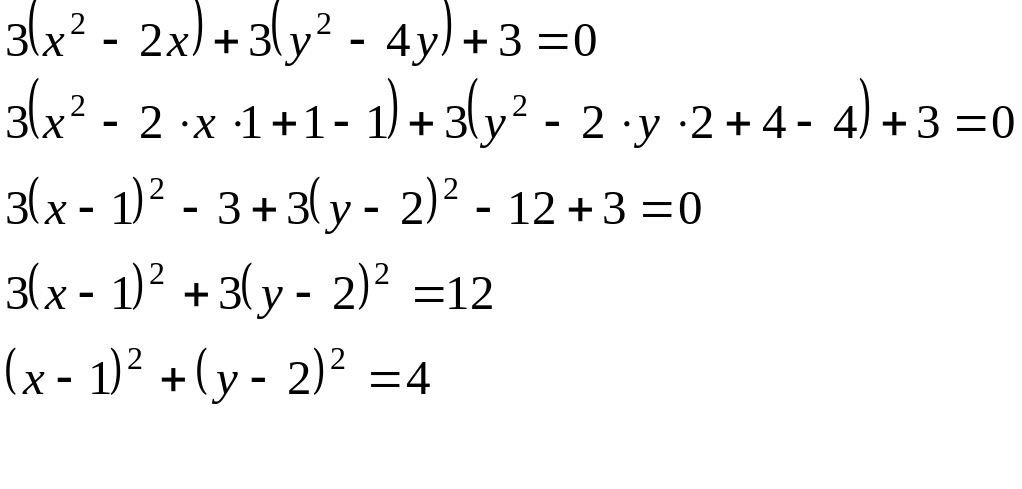
Полученное уравнение определяет окружность с центром в точке (1;2)
и радиусом R=2
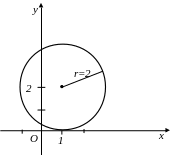
Рис.16.
Пример 7. Определить, какая кривая задана уравнением, найти основные параметры и построить:
![]()
Решение:
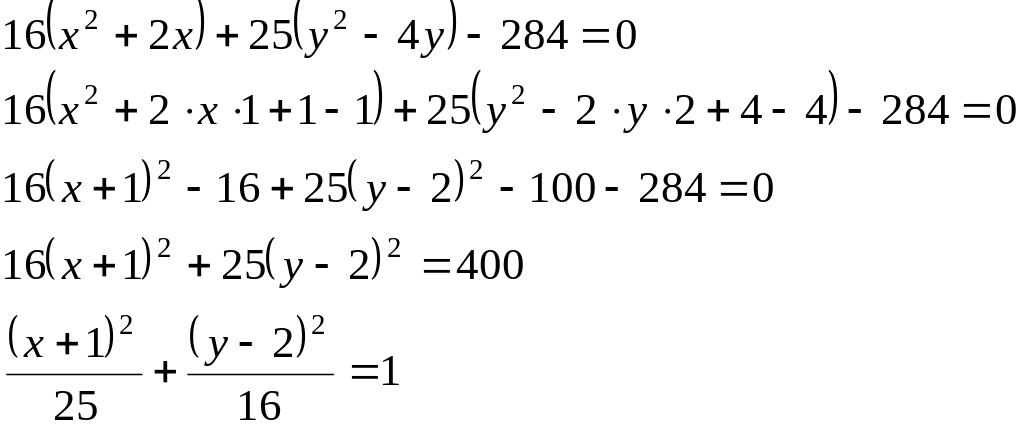
Полученное уравнение определяет эллипс с центром в точке (-1;2); полуоси: a=5 , b=4
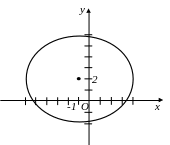
Рис.17.
Пример 8. Определить, какая кривая задана уравнением, найти основные параметры и построить:
![]()
Решение:
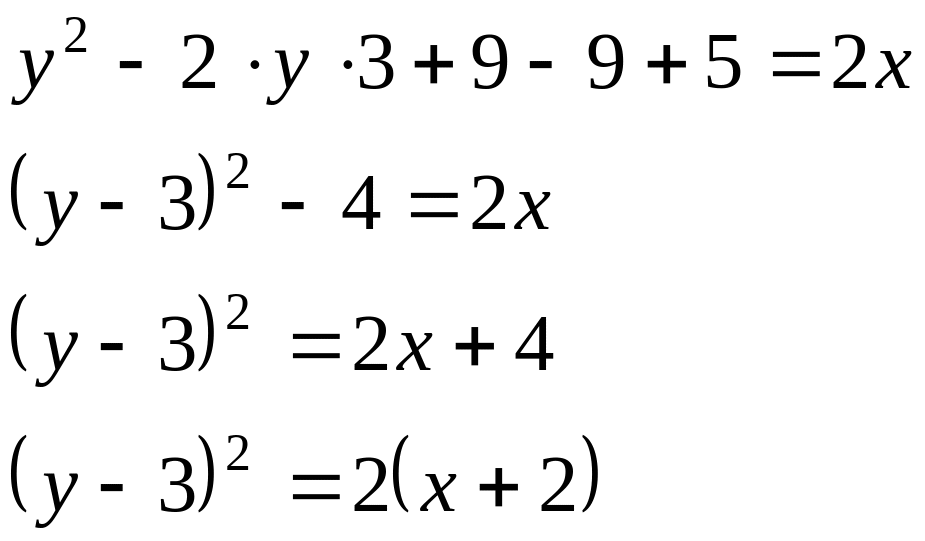
Данное
уравнение определяет параболу
с вершиной в точке (-2;3),
осью симметрии y=3,
ветви в положительном направлении оси
Ох.
Точки пересечения с осью Оу:
х=0, тогда
![]() ;
отсюда у1=1,
у2=5
;
отсюда у1=1,
у2=5
y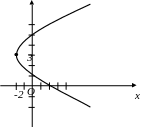
Рис.18.
Пример 9. Определить, какая кривая задана уравнением, найти основные параметры и построить:
![]()
Решение:
![]()
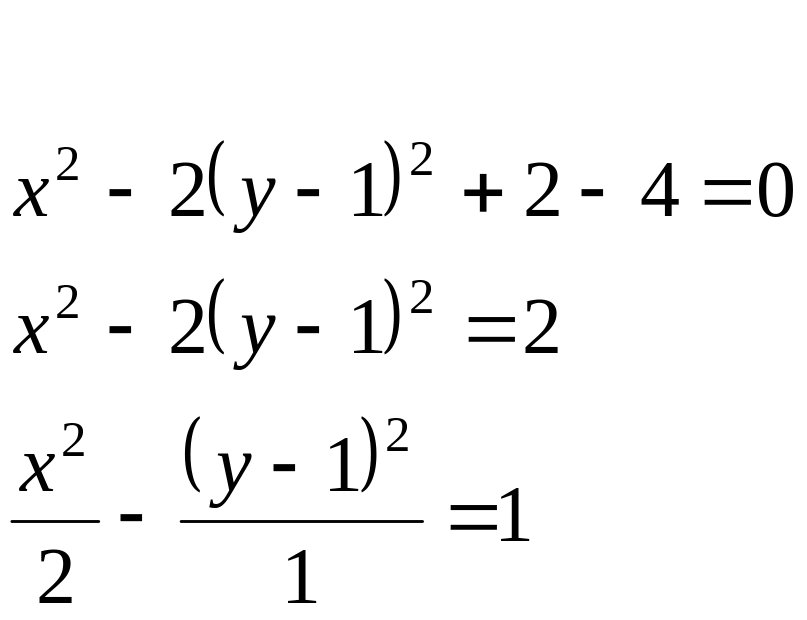
П
y![]() ,
b=1.
,
b=1.
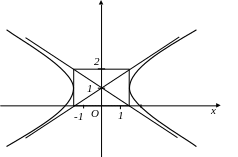
Рис.19.
