27

1. Система координат на плоскости

   1. Основные понятия

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости.

Прямоугольная (декартова) система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный отрезок. Эти оси называются осями координат, точку их пересечения О – началом координат. Ось называют осью абсцисс, ось – осью ординат. Координатами точки М в системе координат называются координаты радиус–вектора . Если , то координаты точки М записывают , число х называется абсциссой точки М, у – ординатой точки М.

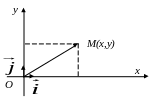
Рис.1.

Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором того же направления, что и луч Ор.

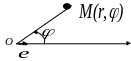
p

Рис.2.

Числа и называются полярными координатами точки М, пишут .

Связь между прямоугольными и полярными координатами:

Рис.3.

Из рисунка видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:

(1)

Полярные координаты точки М выражаются через декартовы координаты:

(2)

Пример 1. Найти прямоугольные координаты точки М с полярными координатами .

Решение. Имеем По формулам (1) находим

Итак, .

2. Линии на плоскости

Уравнением линии (или кривой) на плоскости называется такое уравнение с двумя переменными, которому удовлетворяют координаты и каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные и называются текущими координатами точек линии.

Уравнение называется уравнением данной линии в полярной системе координат, если координаты любой точки , лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать при помощи двух уравнений

,

(3)

где и – координаты произвольной точки , лежащей на данной линии, а – переменная, называемая параметром; параметр определяет положение точки на плоскости. Если параметр меняется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (3) – параметрическими уравнениями линии.

Линию на плоскости можно задать векторным уравнением , где – скалярный переменный параметр. Каждому значению соответствует определенный вектор плоскости. При изменении параметра конец вектора опишет некоторую линию (рис. 4)

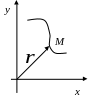
Рис.4

Итак, всякой линии на плоскости соответствует некоторое уравнение вида .

Пример 2. Построить кривую .

Решение. Задавая значения , будем находить значения , результаты сведем в таблицу

	0
	0						0

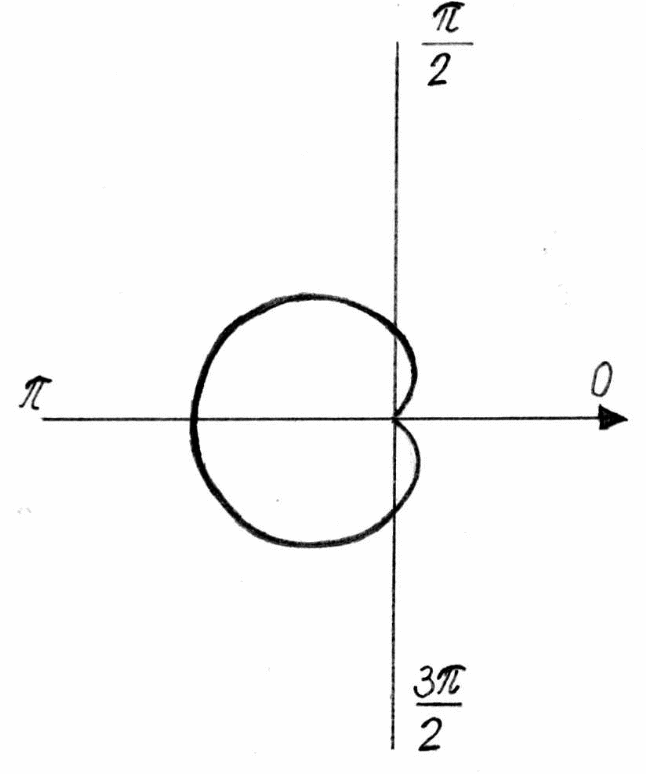
Рис.5.