2.4 Минимизация логических формул

 

Однозначная зависимость сложности логической формулы и функциональной схемы логического устройства приводят к выводу о необходимости минимизации структурной формулы логического устройства. Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики.

 

2.4.1 Расчётный метод минимизации

Применение этого метода состоит в последовательном применении к некоторой формуле законов и правил тождественных преобразований алгебры логики. При этом широко используют следующие приёмы: прибавление одного или нескольких членов, входящих в СДНФ, поскольку X v X v X = X; выделение членов, содержащих множитель ; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм.

Пример: Минимизировать функцию СДНФ мажоритарного элемента (См. п.2.2) и реализовать его схему на элементах основного базиса.

Склеивая первые три минтерма с четвёртым, получаем ДНФ функции мажоритарного элемента, которая проще СДНФ:

Минимизированная функциональная схема мажоритарного элемента приведена на рисунке 7

 

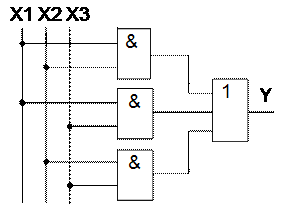
Рисунок 7 Функциональная схема мажоритарного элемента,

реализованная на основе минимизированной функции ДНФ

 

Из сравнения схем, приведённых на рисунках 3 и 7 следует, что в минимизированной схеме число по Квайну уменьшилось с 19 до 9.

 

Метод минимизирующих карт Карно

 

Карты Карно – это графическое представление таблиц истинности логических функций. Они содержат по 2ⁿ ячеек, где n—число логических переменных. Например, карта Карно для функции трёх переменных содержит ячеек, для четырёх переменных-- ячеек.

Карта размечается системой координат, соответствующих значениям входных переменных. Обратим особое внимание на то, что координаты столбцов (а также и строк, если n >3), следуют не в естественном порядке возрастания двоичных кодов, а так: 00 01 11 10. Это делается для того, чтобы соседние наборы (в том числе и столбцов 1 и 4) отличались лишь одной цифрой в каком либо разряде.

Процесс минимизации заключается в формировании правильных прямоугольников, содержащих по 2^к ячеек, где к—целое число. В прямоугольники объединяются соседние ячейки, которые соответствуют соседним элементарным произведениям (т. е. отличаются только в одном разряде).

Несмотря на то, что карты Карно изображаются на плоскости, соседство квадратов устанавливается на поверхности тора. Верхняя и нижняя границы карты как бы склеиваются, образуя поверхность цилиндра. При склеивании боковых границ получается поверхность тора.

Пример: Минимизировать функцию трёх переменных, заданную таблицей истинности (таблица 6).

Таблица 6 Таблица истинности функции трёх переменных

 

X1 X2 X3	Y		X1 X2 X3	Y
0 0 0 0 0 1 0 1 0 0 1 1	0 1 0 1		1 0 0 1 0 1 1 1 0 1 1 1	0 1 0 0

СДНФ функции:

Составляем карту Карно и производим разметку её сторон:

Рисунок 8 Карта Карно функции 3-х переменных.

 

На карте Карно формируем два прямоугольника. Первый из них объединяет (как бы заключает в скобки) два первых минтерма (слагаемых), а второй – первое и третье слагаемые СДНФ минимизируемой функции, приведённой выше. Минтермы, объединённые в прямоугольники, отличаются только в одном разряде. Их неизменяемая часть, которая при минимизации расчётным методом выносится за скобки, и является минимизированным значением функции:

Таким образом, карта Карно позволяет поместить рядом, то есть в соседних ячейках, соседние элементарные произведения, отличающиеся только одним сомножителем.

 

Последовательность действий при минимизации:

1       Изображается карта Карно и производится разметка её сторон.

2                        Ячейки карты Карно, соответствующие наборам переменных, обращающих функцию в «1», заполняются единицами, остальные – нулями.

3                        Выбирается наилучшее покрытие карты прямоугольниками. Наилучшим считается покрытие, образованное минимальным числом прямоугольников, а если таких вариантов несколько, то выбирается тот, который даёт максимальную площадь прямоугольников.

Пример: Минимизировать функцию четырёх переменных, представленную картой Карно: (Рисунок 9)

.

Рисунок 9 Карта Карно функции 4-х переменных

 

Из карты Карно записываем минимизированное значение функции: