2.3 Понятие базиса

 

Любая, сколь угодно сложная логическая функция, представленная таблицей истинности, может быть представлена в форме СДНФ или СКНФ. Каждая из этих формул записана с помощью логического сложения, умножения и отрицания. Поэтому для реализации логических устройств, предназначенных для обработки цифровых сигналов, в общем случае необходимо иметь элементы, выполняющие операции И, ИЛИ, НЕ. Такой набор элементов называется функционально полной системой логических элементов или логическим базисом. Это означает, что из комбинации логических элементов И, ИЛИ, НЕ, взятых в достаточном количестве, можно построить сколь угодно сложное цифровое устройство. Базис из элементов: И, ИЛИ, НЕ называется основным.

Однако, число необходимых элементов в такой системе можно уменьшить, исключив из неё либо элемент ИЛИ, либо элемент И. Например, в соответствии с теоремой де Моргана, имеем Отсюда следует, что операцию логического ИЛИ можно заменить операцией И над инверсными значениями переменных, , а затем к результату применить операцию инверсии и тем самым исключить элемент ИЛИ (Рисунок 4)

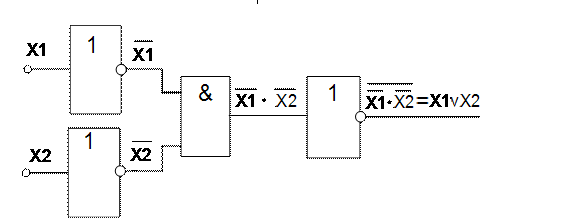
Рисунок 4 Реализация элемента ИЛИ на элементах НЕ, И

 

Аналогично можно исключить элемент И, заменив его операцией логической суммы над инверсными значениями переменных с последующим применением операции инверсии Следовательно, системы, состоящие из двух элементов (ИЛИ, НЕ либо И, НЕ), также являются функционально полными системами и содержат минимальный логический базис.

При схемной реализации функционально полных систем с минимальным логическим базисом идут по пути использования универсальных логических элементов: ИЛИ-НЕ, И-НЕ и И-ИЛИ-НЕ (Рисунок 5

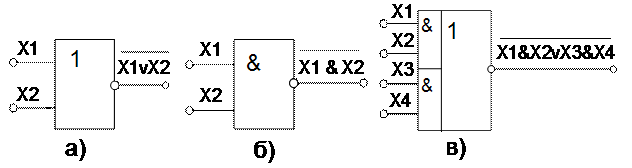
. Рисунок 5 Универсальные логические элементы

 

Элемент ИЛИ-НЕ Рисунок 5,а) осуществляет логическую операцию , называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую операцию и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в) осуществляет операцию и является элементом сложного базиса.

Элементы универсальных базисов позволяют реализовать все три основные логические операции (Рисунок 6). Например, для осуществления операции НЕ с помощью элемента И-НЕ достаточно объединить входы . (рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.

Рисунок 6 Реализация функций НЕ, И и ИЛИ на элементах И-НЕ

 

При последовательном соединении элемента И-НЕ и инвертора осуществляется операция логического умножения: (рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения:

Применение трёх элементов И-НЕ, два из которых работают в режиме инвертирования с объединёнными входами (рисунок 6,в), позволяют реализовать операцию логического сложения . Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения.

В общем случае логическая функция Y может зависеть от нескольких переменных Говорят, что функция Y определена, если известны её значения для всех возможных наборов переменных. Функция Y не определена, когда некоторые сочетания переменных по условию задачи невозможны, В этом случае её можно доопределить, приписав ей значение «1» либо «0» по соображениям удобства реализации.