Основні теоретичні положення

Загальні відомості. Ймовірність приймання помилкового рішення складається із ймовірностей помилкової тривоги і пропуску дефекту. Якщо приписати “ціну” цим помилкам, то одержимо вираз для середнього ризику:

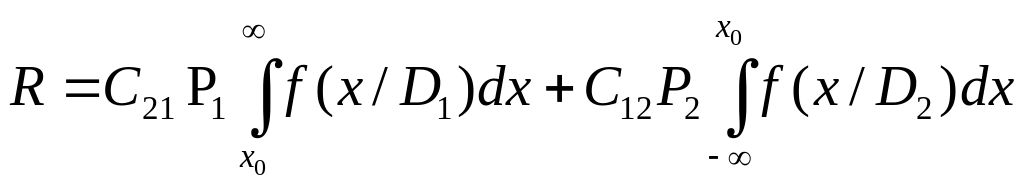
(9.1)

Зрозуміло, що ціна помилки має умовне значення, але вона повинна врахувати можливі наслідки помилкової тривоги і пропуску дефекту. У задачах надійності ціна пропуску дефекту зазвичай значно вища ціни помилкової тривоги ( ). Інколи вводиться ціна правильних рішень і , яка для порівняння з ціною втрат (помилок) приймається від’ємною. У загальному випадку середній ризик (очікувана величина втрат) виражається рівністю

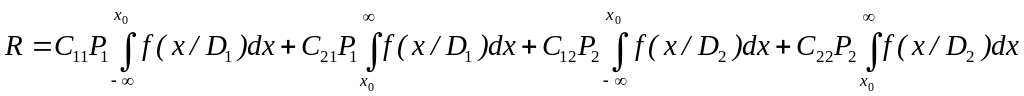(9.2)

Величина х, яка представляється для розпізнавання, є випадковою і тому рівності (9.1) і (9.2) представляють собою середні значення (математичне очікування) ризику.

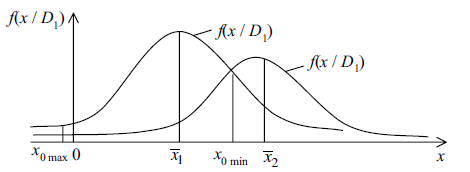
Рисунок 9.1 – Точки екстремуму середнього ризику помилкових рішень

Знайдемо граничне значення х₀ із умови мінімуму середнього ризику. Диференціюючи (9.2) по х₀ і прирівнюючи похідну до нуля, отримуємо спочатку умову екстремуму:

(9.3)

або

(9.4)

Ця умова часто визначає два значення х₀, з яких одне відповідає мінімуму, інше – максимуму ризику (рис.9.1). Співвідношення (9.4) являється необхідним, але недостатньою умовою мінімуму. Для існування мінімуму R у точці х=х₀ друга похідна має бути додатною , що приводить до наступної умови відносно похідних щільностей розподілу:

. (9.5)

Якщо розподіл і являються, як завжди, одно модальними (тобто містить не більше однієї точки максимуму), то при

(9.6)

умова (9.5) виконується. Дійсно, у правій частині рівняння стоїть додатна величина, а при похідна , тоді як за значення .

У подальшому під х₀ будемо розуміти граничне значення діагностичного параметра, що забезпечує за правилом (9.5) мінімум середнього ризику. Будемо також вважати розподіли і одно модальними (“одногорбими”).

Із умови (9.4) випливає, що рішення про віднесення об’єкту х до стану або можна пов’язати з величиною відношення правдоподібності. Пригадаймо, що відношення щільностей ймовірностей розподілу х при двох станах називається відношенням правдоподібності. За методом мінімального ризику приймається наступне рішення про стан об’єкту, який має дане значення параметру х:

, якщо (9.7)

, якщо (9.8)

Ці умови випливають із співвідношень (9.5) і (9.4).

Умова (9.7) відповідає , умова (9.8) . Величина представляє собою порогове значення для відношення правдоподібності. Пригадаємо, що діагноз відповідає справному стану, - дефектному стану об’єкту; - ціна помилкової тривоги; - ціна пропуску мети (перший індекс – прийнятий стан, другий - дійсний); ; - ціна правильних рішень (умовні виграші). У більшості практичних задачах умовні виграші (заохочення) для правильних рішень не вводяться і тоді

(9.9)

Часто виявляється, що зручно розглядати не відношення правдоподібності, а логарифм цього відношення. Це не змінює результату, так як логарифмічна функція зростає монотонно разом зі своїм аргументом. Розрахунок для нормального і деяких інших розподілів при використанні логарифму відношення правдоподібності виявляється дещо простішим.

Розглянемо випадок, коли параметр х має нормальний розподіл за справного і несправного станах. Розсіяння параметра (величина середньоквадратичного відхилення) приймається однаковим.

У розглянутому випадку щільності розподілів

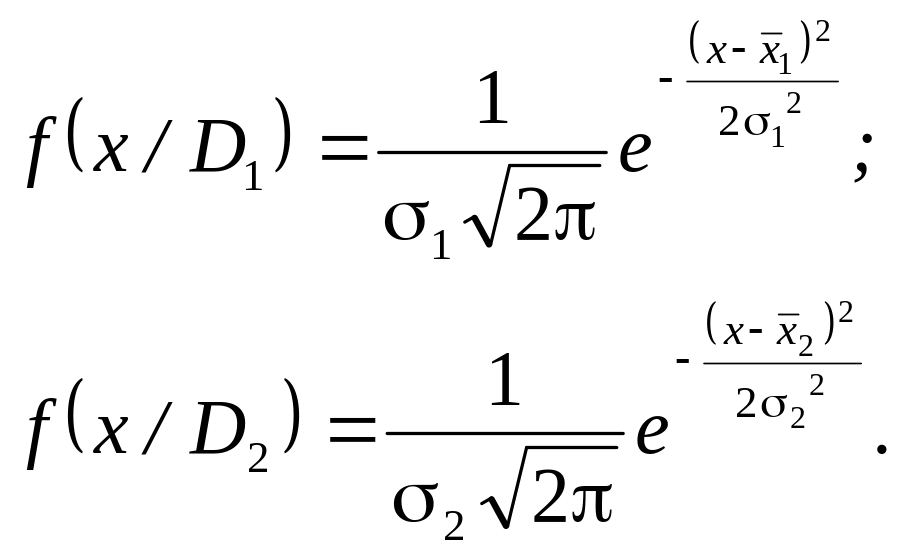
Вносячи це співвідношення у рівняння (9.4), отримуємо після логарифмування

Із цього рівняння

При _{, ,}

Приклад. Діагностування стану трансмісії газотурбінного двигуна здійснєються за вмістом заліза у маслі. Для справного стану середнє значення складає (5 г заліза на 1 т масла) і середньоквадратичне відхилення . За наявності дефекту підшипників та інших деталей (несправний стан) ці значення рівні . Розподіли вважаються нормальними.

Необхідно визначити граничний вміст заліза у маслі, вище якого двигун підлягає зніманню з експлуатування і розбиранню (щоб уникнути небезпечних наслідків). За статистичним даними несправний стан трансмісії спостерігається у 10% двигунів.

Приймемо, що відношення ціни пропуску цілі і помилкової тривоги і відмовимося від “винагороди” правильних рішень ( ). Із умови (9.4) отримуємо

Щільності розподілу

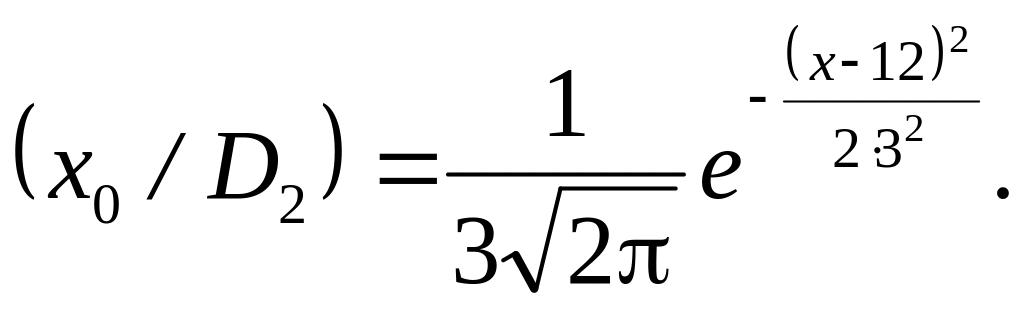
Уносячи ці значення у попереднє рівняння, отримуємо після логарифмування:

Дане рівняння має додатній корінь

ПОРЯДОК ВИКОНАННЯ роботи

1. Вивчити методичні вказівки і отримати завдання (додаток А).

2. Розрахувати граничний стан діагностичного параметра, вище якого досліджуваний об’єкт підлягає зніманню з експлуатації за методом мінімального ризику.

3. Оформити звіт по практичній роботі. Оформити висновки.

4. Захистити звіт по практичній роботі при співбесіді з викладачем.

Запитання до самоконтролю

9.1 У чому полягає метод мінімального ризику?

9.2 Яку попередню інформацію необхідно мати для розрахунку граничного стану діагностичного параметра за методом мінімального ризику?

9.3 Від чого залежить ймовірність приймання помилкового рішення щодо встановлення діагнозу?

9.4 Як визначається відношення правдоподібності?