Глава 2. Операторный метод расчета переходных процессов

2.1. Общие замечания

Операционное исчисление в настоящее время широко применяется в самых различных областях науки и техники. Особенно большую роль оно играет при исследовании переходных процессов в линейных физических системах электротехники, автоматики, радиотехники, механики и других отраслей знаний.

Для инженерных расчетов более удобным является операторный метод решения линейных дифференциальных уравнений высокого порядка, при котором заданные независимые начальные условия включаются в исходные уравнения и для нахождения искомых функций не требуется определять постоянные интегрирования.

Операторный метод заключается в том, что из области функций действительного переменного решение переносятся с помощью преобразований Лапласа в область функций комплексного переменного р. При этом исходные дифференциально-интегральные уравнения переводятся в алгебраические операторные, что позволяет свести расчет к решению системы алгебраических уравнений. Затем, полученный решением алгебраических уравнений результат переводится в область функций действительного переменного.

2.2. Преобразование Лапласа и его применение к расчету переходных процессов

Если функция f(t) = 0 при t<0, а при t≥0е возрастает или растёт не быстрее показательной функции, т.е. (С_о называют порядком роста функции f(t)), то для неё существует изображение по Лапласу

,

где

f(t) - оригинал, функция действительного переменного

F(t) - изображение функции-оригинала f(t), функция комплексного переменного р = с + jw. Между функцией-оригиналом и её изображением имеет место взаимно однозначное соответствие.

С оответствие между изображением и оригиналом будем обозначать и записывать

F (p) f(t) или f(t) F(p)

Простейшими оригиналами являются единичная и показательная функции.

Единичная функция (рис.2.0), заданная условием

соответствует случаю включения постоянной э.д.с., равной 1 В.

Рис. 2.0

Единичная функция имеет условное обозначение l(t). Изображение единичной функции имеет вид:

Следовательно,

f (t)

Многие функции становятся оригиналами при умножении на единичную функцию, что делает функцию равной нулю при t<0. Принято единичную функцию не записывать, но подразумевать.

Единичная функция может рассматриваться при t>0 как экспонента е^qt с показателем q=0.

В качестве примера изображение экспоненты f(t)= е^qt имеет вид

Причем Re p > Re q, иначе интеграл расходится.

В силу линейности операций интегрирования [5, с. 200] ступенчатая (постоянная) функция Е=const имеет изображение Е/р.

С помощью прямого преобразования получена таблица изображений функций по Лапласу [3]. Операторные изображения некоторых функций приведены в табл. 1. Основные свойства одностороннего преобразования Лапласа приведены в табл. 2.

2.3. Изображение элементов цепи

Используя преобразование Лапласа, изображения производной, интеграла и свойство линейности [табл.2], можно записать изображения напряжений на активном сопротивлении

U _r(t)=r^.i(t) r^.I(p)=U_r(p)

на индуктивности

на емкости

Приведенным изображающим уравнениям для элементов электрической цепи можно поставить в соответствие изображающие операторные схемы (рис. 2.1).

Таблица 1

№ п/п

Оригинал

Изображение

1	2	3
1.	Е=const	Е/р
2.	l(t)	l/h
3.	δ(t)	1
4.	t	p-2
5.
6.
7.
8.
9.
10.
11.
12.	cos ω.t
13.	sin ω.t
14.	cos (ω.t+Ψ)
15.	sin (ω.t+Ψ)
16.
17.
18.
19.
20.

Таблица 2

№ п/п

Наименование

Формула

1	2	3
1.	Свойство линейности
2.	Дифференцирование оригинала
3.	Изменение масштаба независимого переменного (теорема подобия)
4.	Интегрирование оригинала
5.	Смещение в области действительного переменного (теорема запаздывания)
6.	Смещение в области комплексного переменного (теорема смещения)
7.	Предельные соотношения: начальное значение оригинала,
	конечное значение оригинала
8.	Умножение изображения (теорема свертывания)
9.	Интеграл Дюамеля (следствие теоремы свертывания)

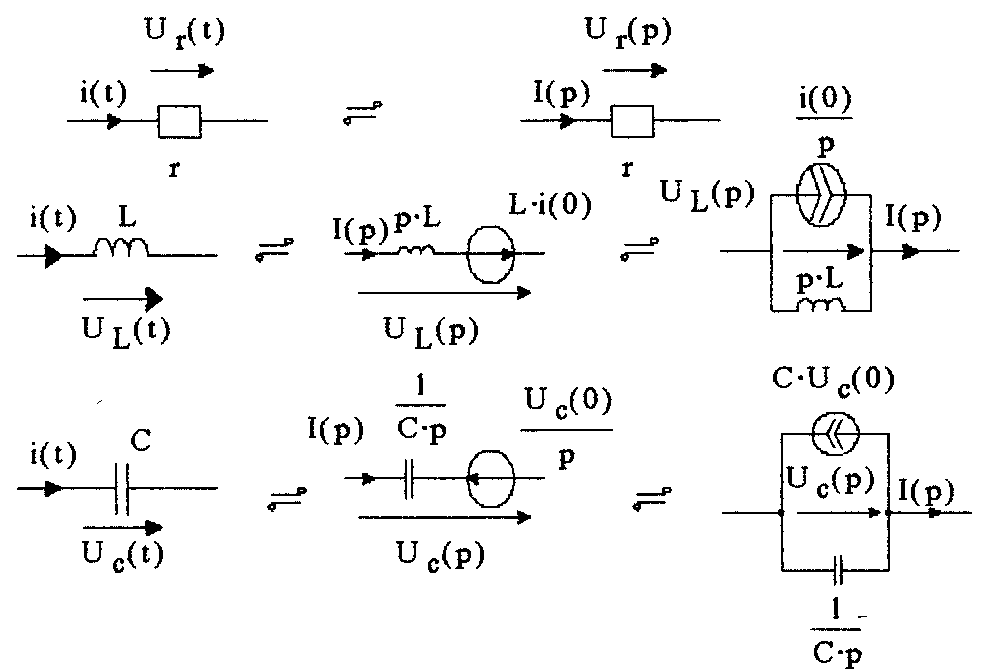
Рис. 2.1

Величина L i(0) представляет собой внутреннюю э.д.с., обусловленную запасом энергии в магнитном поле индуктивности L вследствие протекания через нее тока i(0) непосредственно до коммутации.

Величина Uc(0)/p представляет собой внутреннюю э.д.с., обусловленную запасом энергии в электрическом поля конденсатора вследствие наличия напряжения на нем Uc(0) непосредственно до коммутации. Заметим, что L i(0) на схеме направляется по току, a Uc(0)/p - против тока.

Величины pL и 1/Ср можно рассматривать как операторные сопротивления и ёмкости.