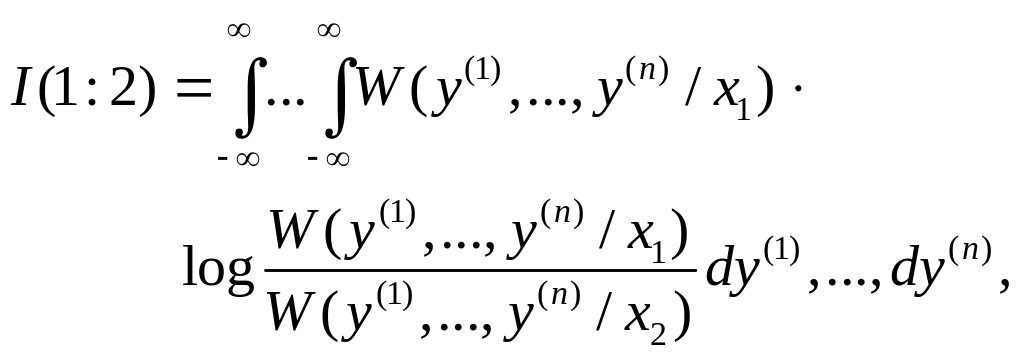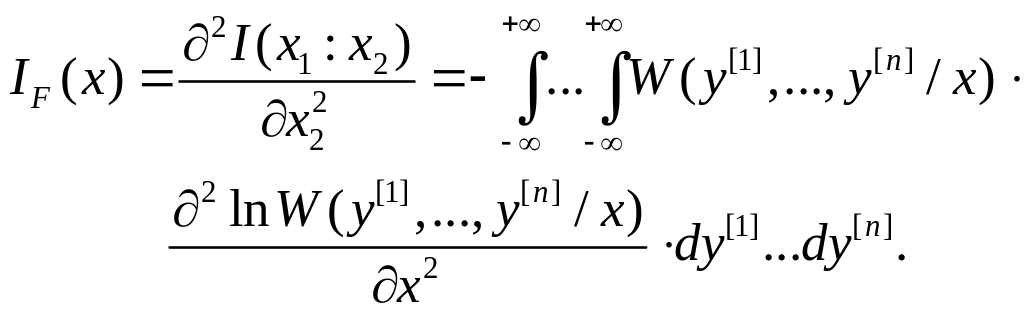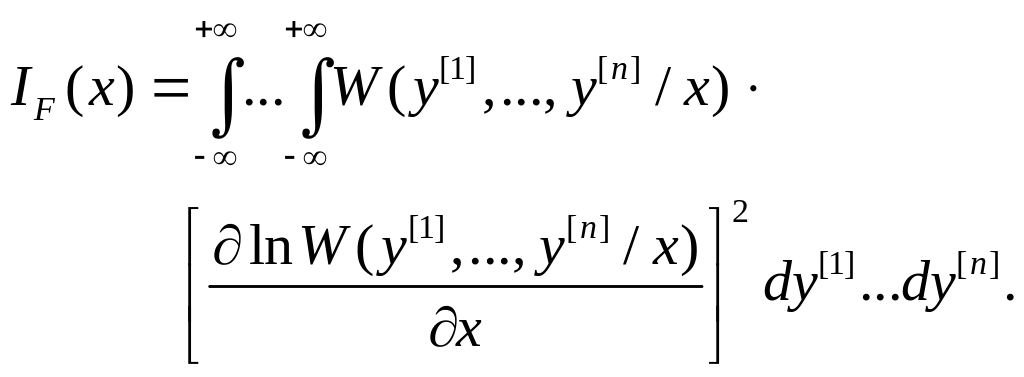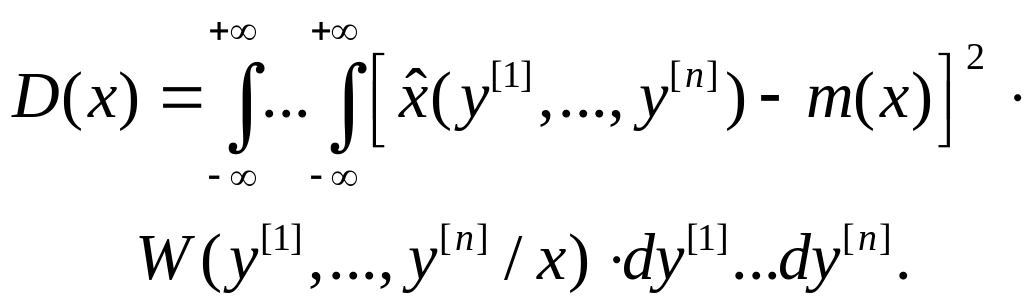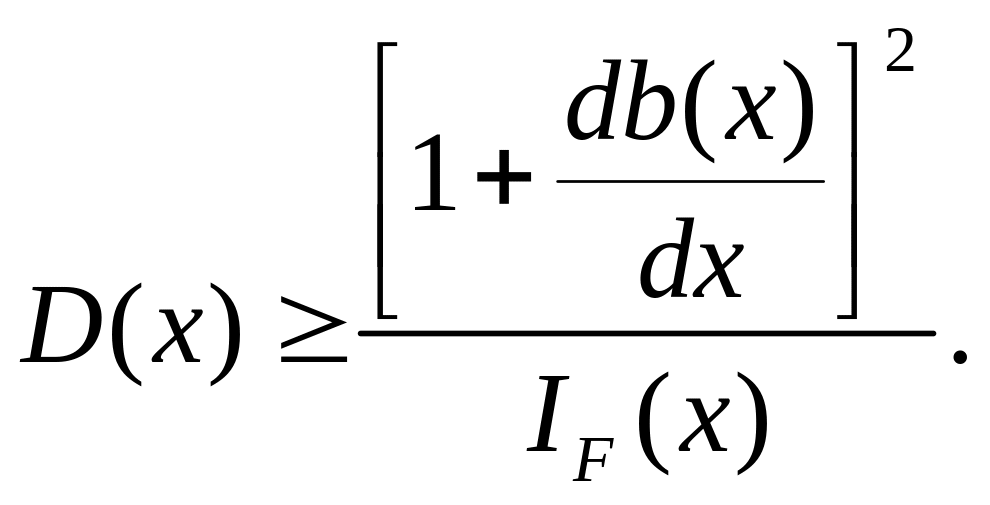5.2 Информация по Фишеру
Определение.
Свойства. Пусть
сообщение X
есть непрерывная случайная величина,
а сигнал
![]() характеризуется условной плотностью
вероятности
характеризуется условной плотностью
вероятности
![]() Рассмотрим две гипотезы:
Рассмотрим две гипотезы:
H1
– передано сообщение x1,
то есть
![]() ,
,
H2
– передано
сообщение x2,
то есть
![]() .
.
Среднюю информацию в пользу H1, вычисленную по формуле (5.1.2)
|
(5.2.1) |
можно формально рассматривать как функцию аргумента x2, зависящую от параметра x1. На рис.5.2 в качестве примера приведен возможный вид этой функции при различных значениях x1.
Е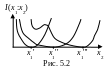 сли
существует вторая производная этой
функции по x2 в
точке x2= x1=
x,
сли
существует вторая производная этой
функции по x2 в
точке x2= x1=
x,
|
(5.2.2) |
то ее величина называется информацией по Фишеру о параметре x, содержащейся в сигнале y.
То же значение информации можно получить в результате вычисления по формуле
|
(5.2.3) |
Выбор одной из
двух формул определяется только удобством
вычислений. Информация Фишера показывает,
насколько быстро возрастает функция
I(x1:x2)
при увеличении
![]() и, следовательно, является мерой
различимости близких значений x1
и x2.
и, следовательно, является мерой
различимости близких значений x1
и x2.
Информация Фишера, как и информация Кульбака, обладает свойствами выпуклости и аддитивности. Единицы измерения информации Фишера – это единицы измерения величины х-2.
Неравенство Рао-Крамера. Это – главный результат теории информации по Фишеру.
Рассмотрим задачу
оценки непрерывного сообщения x.
Правило оценивания сводится к тому, что
каждому значению выборки
ставится в соответствие некоторое
значение оцениваемого параметра x.
Таким образом, оценка
![]() является функцией выборочных данных и
поэтому также является случайной
величиной. Обычно вычисляют следующие
числовые характеристики оценки:
является функцией выборочных данных и
поэтому также является случайной
величиной. Обычно вычисляют следующие
числовые характеристики оценки:
1) Математическое ожидание при условии, что истинное значение сообщения равно x,
|
(5.2.4) |
2) Смещение
|
(5.2.5) |
т.е. систематическую ошибку, сопутствующую выбранному правилу оценивания.
3) Дисперсию, вычисляемую также при условии, что истинное значение сообщения равно x,
|
(5.2.6) |
Дисперсия оценки является основной количественной мерой точности оценивания.
Пусть функция
правдоподобия
![]() дифференцируема по параметру x,
информация Фишера (5.2.2) существует и не
равна нулю для всех значений параметра
в окрестности точки x,
тогда дисперсия и смещение любой оценки
связаны с информацией Фишера неравенством
Рао-Крамера
дифференцируема по параметру x,
информация Фишера (5.2.2) существует и не
равна нулю для всех значений параметра
в окрестности точки x,
тогда дисперсия и смещение любой оценки
связаны с информацией Фишера неравенством
Рао-Крамера
|
(5.2.7) |
Для несмещенных оценок (b(x)=0) или для оценок с постоянным, не зависящим от x смещением (b(x)=c), числитель в (5.2.7) равен единице и тогда
|
(5.2.8) |
Таким образом, информация Фишера является количественной мерой предельной, потенциальной точности оценивания непрерывного сообщения x, так как дисперсия несмещенной оценки не может быть меньше величины, обратной информации Фишера.
Неравенства (5.2.7) и (5.2.8) обращаются в равенства тогда и только тогда, когда одновременно выполняются два условия:
1) Функция правдоподобия выборки может быть представлена в виде
|
(5.2.9) |
где
![]() – некоторая функция выборки y,
не зависящая от x
и
– некоторая функция выборки y,
не зависящая от x
и
![]() ,
,
![]() – функция, зависящая
только от x
и
– функция, зависящая
только от x
и
![]() .
Оценка
,
удовлетворяющая условию (5.2.9), называется
достаточной, поскольку она сохраняет
всю информацию о x,
содержащуюся в самой выборке.
.
Оценка
,
удовлетворяющая условию (5.2.9), называется
достаточной, поскольку она сохраняет
всю информацию о x,
содержащуюся в самой выборке.
Функция правдоподобия выборки такова, что для любого x выполняется соотношение
|
(5.2.10) |
где
![]() – некоторая функция x.
– некоторая функция x.
Оценка, удовлетворяющая этому уравнению, называется эффективной, а семейство распределений, задаваемых уравнением (5.2.10) при различных значениях x, называется экспоненциальным семейством. Легко убедиться, что эффективная оценка всегда достаточна, но обратное утверждение неверно.
Среди всех оценок с заданным смещением именно эффективные оценки обладают минимальной дисперсией. К сожалению, эффективная оценка существует далеко не во всех случаях, и тогда потенциальная точность оценивания сообщения недостижима.
Оценка максимального
правдоподобия. Метод максимального
правдоподобия широко используется на
практике. В качестве оценки
выбирается такое значение x,
при котором функция правдоподобия
![]() достигает наибольшего значения. Это
значит, что в качестве оценки максимального
правдоподобия выбирается решение
уравнения правдоподобия
достигает наибольшего значения. Это
значит, что в качестве оценки максимального
правдоподобия выбирается решение
уравнения правдоподобия
|
(5.2.11) |
Доказано, что если эффективная оценка существует, то она может быть реализована методом максимального правдоподобия.