3.3 Информационные характеристики непрерывных случайных функций

Имеются два различных способа определения информации-онных характеристик непрерывных стационарных случайных функций.

Первый способ предусматривает квантование во времени исходной непрерывной случайной функции X(t) и переход к последовательности непрерывных случайных величин-отсчётов …, X ,X ,X ,…, взятых через интервалы , где - ширина полосы частот на положительной полуоси, занимаемых спектром плотности мощности этой функции. Для полученной непрерывной последовательности вводятся характеристики, аналогичные тем, которые были введены для дискретных последовательностей (формулы (2.4.1) – (2.4.3), (2.4.6) – (2.4.10)), но используется понятие относительной энтропии.

Определённая таким образом энтропия непрерывной случайной величины функции X(t) равна средней относительной энтропии, приходящейся на один отсчёт. Эта величина также удовлетворяет неравенствам (2.4.3) и (2.4.4), причём в качестве H используется максимальное значение относительной энтропии непрерывной случайной величины при заданных ог-раничениях. Например, если задана средняя мощность σ² слу-чайной функции X(t), оба неравенства совместно дают

,

(3.3.1)

причём максимальной относительной энтропией на один отсчёт обладает нормальная случайная функция с нулевым математическим ожиданием, дисперсией (средней мощностью) и равномерным в полосе энергетическим спектром (белый шум).

«Энтропийной мощностью» случайной функции X(t), имеющей ширину спектра и энтропию Н нат/отсчёт, называется средняя мощность белого шума с такой же шириной спектра и тем же значением энтропии на отсчёт

.

(3.3.2)

Относительная энтропия на один отсчёт нормальной случайной функции, имеющей спектр плотности мощности G(f), вычисляется по формуле

,

(3.3.3)

а энтропийная мощность равна

.

(3.3.4)

Второй способ введения энтропийных характеристик случайной функции опирается на понятие точности воспроизведения реализации этой функции. Пусть x(t) есть реализация непрерывной случайной функции X(t), которую необходимо передать, а z(t) – реализация другой случайной функции Z(t), которая в действительности принимается. Обозначим как некоторую заранее заданную количественную меру различия этих двух случайных функций. Тогда -энтропией случайной функции X(t) называется минимальное среднее количество взаимной информации в единицу времени между X(t) и Z(t), необходимое для того, чтобы .

Часто в качестве меры отличия используют среднеквадратическую ошибку воспроизведения стационарной случайной функции X(t) при помощи стационарной и стационарно свя-занной с ней случайной функции Z(t)

.

(3.3.5)

Если Z(t) – это цифровой сигнал, то -энтропия численно равна минимальному среднему количеству двоичных символов в единицу времени, необходимых для восстановления функции X(t) со среднеквадратической ошибкой, не превышающей .

Для нормальной стационарной случайной функции X(t), имеющей спектр плотности мощности G(f), -энтропия при среднеквадратическом критерии точности (3.3.5) вычисляется по формуле

,

(3.3.6)

где - полоса частот, в которой . Коэффициент выбирается таким образом, чтобы площадь фигуры, ограниченной снизу осью f, а сверху – прямой G= (в области ) либо кривой G(f) (вне области ), была равна . Эта фигура заштрихована на рис. 3.3.1.

П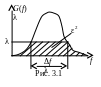 онятие - энтропии может быть применено и к последовательности дискретных случайных величин.

При вычислении -энтропии случайной величины X, когда расстояние между X и Z задано в виде математического ожидания некоторой функции

(3.3.7)

их разности V=X-Z, справедливо соотношение

.

(3.3.8)

Оно показывает, что средняя условная энтропия ошибки при заданном ограничении достигает максимального значения, когда X и Z независимы. Это требование, однако, не является достаточным.