
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Г лава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца. Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
19. Ортогональные системы функций и ряды Фурье
19.1. Некоторые свойства оператора Лапласа. Рассмотренные выше граничные задачи (18.1) и (18.11), а также задачи (18.41), (18,42) и ряд других можно кратко сформулировать в виде
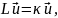 (19.1)
(19.1)
где
 2
- взятый с обратным знаком оператор
Лапласа, параметр к - это k2
или χ 2 (в. зависимости от
того, является ли задача трёхмерной или
двумерной), а
2
- взятый с обратным знаком оператор
Лапласа, параметр к - это k2
или χ 2 (в. зависимости от
того, является ли задача трёхмерной или
двумерной), а
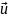 – векторные или
скалярные (
= и)
функции,
подчинённые требуемым граничным
условиям. Обычно граничные условия
задаются вместе
с оператором L;
они определяют
класс функций и,
на которые
может распространяться действие L,
т. е. область
определения оператора DL.
Разумеется, функции
,
принадлежащие этому
классу (кратко пишут:
– векторные или
скалярные (
= и)
функции,
подчинённые требуемым граничным
условиям. Обычно граничные условия
задаются вместе
с оператором L;
они определяют
класс функций и,
на которые
может распространяться действие L,
т. е. область
определения оператора DL.
Разумеется, функции
,
принадлежащие этому
классу (кратко пишут:
 Dl
), должны
допускать заданные операции
дифференцирования. Говорят, что запись
(19.1) выражает общую формулировку задачи
на собственные значения
оператора L. В
частности если и = 0 на S
для
Dl,
получаем задачу (18.1), если иτ
= 0 и div
= 0 на S для
Dl
- задачу (18.41), и т. д.
Dl
), должны
допускать заданные операции
дифференцирования. Говорят, что запись
(19.1) выражает общую формулировку задачи
на собственные значения
оператора L. В
частности если и = 0 на S
для
Dl,
получаем задачу (18.1), если иτ
= 0 и div
= 0 на S для
Dl
- задачу (18.41), и т. д.
Введём интегральную величину, имеющую своё обозначение:
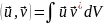 (19.2)
(19.2)
Здесь подразумевается область V
трёхмерной задачи, а в случае задачи
двумерной интегрирование производится
по её области S; величина
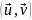 называется скалярным произведением
функций
называется скалярным произведением
функций
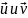 ,
последние
могут быть как векторами, так и
скалярами. Заметим, что (v,
и) = (и, v) *.
,
последние
могут быть как векторами, так и
скалярами. Заметим, что (v,
и) = (и, v) *.
Оператор L, обладающий
тем свойством, что для
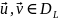
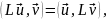 (19.3)
(19.3)
является по определению симметрическим. Легко убедиться, что для всех поставленных в п.18 задач оператор 2 симметрический.
Действительно, в случае скалярных uиv на основании первой формулы Грина (5.13)
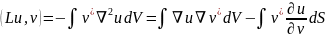 (19.4)
(19.4)
Как для первой граничной задачи (18.1) (и
= 0, v = 0 на S),
так и для второй задачи (18.11)
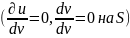 поверхностный интеграл в (19.4) равен
нулю. Меняя местами u и
v*, мы оставляем правую
часть (19.4) неизменной, а потому
поверхностный интеграл в (19.4) равен
нулю. Меняя местами u и
v*, мы оставляем правую
часть (19.4) неизменной, а потому
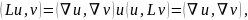 (19.4а)
(19.4а)
т. е. равенство (19.3) выполняется.
Взяв векторные , получаем:
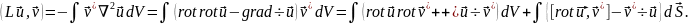 (19.5)
(19.5)
(были использованы формулы векторного анализа (5.12), (5.10), (5.9) и (3.8)).
Если функции
подчинены граничным условиям задачи
(18.41) (uτ
= 0, div
= 0 и vτ
= 0, div
= 0 на S) или граничным
условиям задачи (18.42) (uτ
= 0, (rot
)τ
= 0 и vτ
= 0, (rot
)τ
= 0 на S), то
поверхностные
интегралы в (19.5) равны нулю, и правая
часть остается неизменной при замене
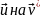 и
обратно. Поэтому
и
обратно. Поэтому
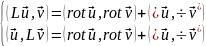 ,
(19.5a)
,
(19.5a)
и выполняется равенство (19.3).
Установленное свойство (19.3) сохраняется и для двумерных областей, т. е. при замене V на S, а граничной поверхности S объема V на контур L поверхности S. Читателю рекомендуется проверить это в качестве упражнения.
Нетрудно убедиться, что собственные значения задачи (19.1) при симметрическом операторе 2 вещественны и неотрицательны. Образуя в (19.1) слева и справа скалярные произведения с , имеем:
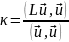 (19.6)
(19.6)
Знаменатель
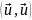 положителен. В силу (19.3)
положителен. В силу (19.3)
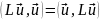 ,
и в то же время
,
и в то же время
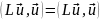 *.
Отсюда следует, что числитель
*.
Отсюда следует, что числитель
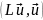 - величина вещественная. Следовательно,
вещественны и собственные значения
- величина вещественная. Следовательно,
вещественны и собственные значения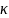
Рассматривая отдельно скалярные и векторные задачи, числитель в (19.6) преобразуем при помощи соотношений (19.4а) и (19.5а). Мы видим, что
 (19.7)
(19.7)
и
 (19
8)
(19
8)
Итак, собственные значения κ = κi задачи (19.1) неотрицательны и могут быть расположены в следующем порядке:
 (19.9)
(19.9)
19.2. Ортогональные системы функций. Две функции и и v называются oртогональными, если их скалярное произведение равно нулю:
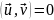 . (19.10)
. (19.10)
Пусть
 (i
= 1, 2, ...) -
собственные функции задачи (19.1), которым
соответствуют собственные значения κ;
предположим, что все κi
различны, или, как говорят, отсутствует
вырождение.
Взяв две любые собственные функции
(i
= 1, 2, ...) -
собственные функции задачи (19.1), которым
соответствуют собственные значения κ;
предположим, что все κi
различны, или, как говорят, отсутствует
вырождение.
Взяв две любые собственные функции
 ,
перепишем
формулировку (19.1):
,
перепишем
формулировку (19.1): 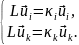
Образуя скалярные
произведения ( ,
,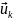 )
и (
)
и (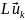 ,
)
и принимая во внимание вещественность
собственных значений, получаем:
,
)
и принимая во внимание вещественность
собственных значений, получаем:
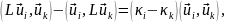
или, в силу симметричности L
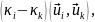 = 0, (19.11)
= 0, (19.11)
а отсюда следует,
что
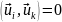 ,
т. е собственные
функции иi
ортогональны.
,
т. е собственные
функции иi
ортогональны.
Задача на собственные значения (19.1)
порождает, таким образом,
ортогональные
системы
функций
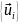 .
.
Ортогональная система
всегда может быть нормирована, т. е.
можно так подобрать постоянные
коэффициенты в выражениях
,
что
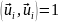 для всех i. Тогда
получается
ортонормированная система, для которой
для всех i. Тогда
получается
ортонормированная система, для которой
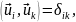 (19.12)
(19.12)
где δik= 0 при i ≠ к и δik = 1 при i = k (символ Кронекера). Путём проверки нетрудно убедиться, что различные собственные функции, полученные в п.18, образуют ортогональные системы. Возьмём, например, систему функций итпр (18.14):
 .
.
Скалярное произведение двух функций
итпр и
 имеет вид:
имеет вид:

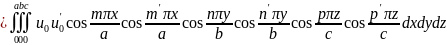
(i и k надо понимать как совокупность чисел т, п, р и т', п', р' соответственно). Поскольку
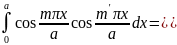
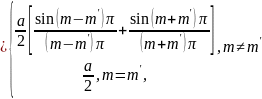
и таковы же интегралы
по у и
z,
то, как видно,
скалярное произведение
действительно обращается в нуль при i
≠
k
(т. е. т
≠ т', п ≠
п' и р ≠ р').
Отсюда же следует, что система
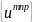 будет
ортонормированной, если взять
будет
ортонормированной, если взять
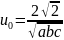
при т ≠
0, п ≠
0, р ≠
0. Когда среди чисел т, п и р
имеются нули, и0 столько
раз делится на
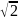 ,
каково число нулей (один, два или три).
,
каково число нулей (один, два или три).
Предлагаю при помощи формул (16.24) и (16.26) проверить ортогональность и ввести нормировку функций ипт (18.29). При этом следует отдельно рассматривать функции с С ≠ 0, D = 0 и С = 0, D ≠ 0 (либо Q ≠ 0, Т = 0 и Q = 0,T ≠ 0).
19.3. Ортогональные
ряды. Взяв ортонормированную систему
функций
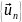 и некоторую функцию
и некоторую функцию
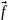 ,
определённую в той же области,
построим ряд
,
определённую в той же области,
построим ряд
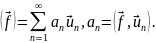 (19.13)
(19.13)
Он называется ортогональным рядом, или рядом Фурье функции , а ап - коэффициентами Фурье.
Отличительным
свойством ряда Фурье
 является
выполнение равенства
является
выполнение равенства
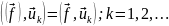 (19.14)
(19.14)
Действительно, составляя в (19.13) скалярное произведение с , справа получаем нуль во всех членах кроме k-го, который дает аk; равенство (19.13) превращается в выражение коэффициента Фурье аk.
Говорят, что ряд Фурье сходится в среднем к , а система {ип} полна (в этом смысле), если
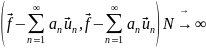 0
(19.15)
0
(19.15)
Системы собственных функций оператора
Лапласа обладают указанным
свойством полноты при всевозможных
функциях
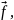 которые приходится рассматривать
практически (например, с разрывами
второго рода).
которые приходится рассматривать
практически (например, с разрывами
второго рода).
Легко убедиться, что обычные тригонометрические ряды Фурье дают частный пример ряда (19.13).
Возьмём, например,
систему собственных функций одномерного
оператора Лапласа из п.7.2. После нормировки
в (7.9)
 ,
и система принимает вид:
,
и система принимает вид:
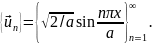
По этой системе разложим некоторую функцию f(x), определённую на отрезке 0 ≤ х ≤ а. Согласно (19.13)
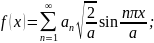
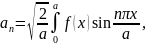 а
это и есть обычный тригонометрический
ряд Фурье по синусам.
а
это и есть обычный тригонометрический
ряд Фурье по синусам.
В качестве второго
примера рассмотрим ряд Фурье типа
(12.22). В данном
случае разлагается определённая на
отрезке –T/2
≤ t
≤ T/2
функция
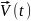 ,
по ортонормированной системе
,
по ортонормированной системе

Ряд (19.13) имеет вид

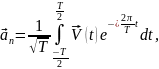
что совпадает с (12.22), (12.23). Заметим, что
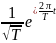 - это собственные
функции одномерного оператора Лапласа
- это собственные
функции одномерного оператора Лапласа
 при периодических граничных условиях
и (-Т/2) = и(Т/2).
при периодических граничных условиях
и (-Т/2) = и(Т/2).
