
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Г лава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца. Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
ФГОБУ ВПО СИБГУТИ
Специальные главы математики
Учебное пособие по курсу «Электромагнитные поля и волны»
Н
овосибирск, 2012г.
Введение
Математика играет важную роль в исследовании различных физических объектов, представляя собой по сути «язык» любой физической теории. Без использования этого специального языка изложение теории электромагнитного поля было бы весьма затруднительно, не говоря уже о применении теории электромагнетизма в практических приложениях.
В данном пособии излагаются математические сведения, необходимые для последующего изучения курса «Электромагнитные поля и волны». Будут изложены вопросы, частично знакомые вам в результате предшествующих курсов математики, однако их более глубокое изучение представляется весьма полезным.
Это касается теории векторных полей, векторных дифференциальных операторов, дифференциальных уравнений с частными производными, некоторых методов математической физики, теории гармонических колебаний, волновых уравнений, краевых задач электродинамики и вычислительных методов.
Глава 1. Элементы векторного анализа
Физические величины могут характеризоваться не только их числовым значением (например, масса, температура) – тогда они называются скалярами, но и направлением в пространстве (например, скорость, сила). Такие величины называются векторами. К этому классу физических величин относятся и характеристики электромагнитного поля - напряжённости, изучаемые в курсе электродинамики. Поэтому эти характеристики описываются с помощью математической теории векторных полей.
1. Векторы и действия над ними
1.1 Основные операции.
Произвольный вектор
 можно
представить как
можно
представить как
 где
где
 -
единичный вектор (орт), а A
- абсолютное значение вектора
.
Орты, соответствующие направлениям
осей декартовой системы координат,
будем обозначать
-
единичный вектор (орт), а A
- абсолютное значение вектора
.
Орты, соответствующие направлениям
осей декартовой системы координат,
будем обозначать
 .
Таким образом, в проекциях на эти оси
вектор
имеет следующий вид:
.
Таким образом, в проекциях на эти оси
вектор
имеет следующий вид:
 . (1.1)
. (1.1)
Проекции вектора
на
оси координат
 называются также его компонентами, или
составляющими вектора.
называются также его компонентами, или
составляющими вектора.
Сложение в векторной алгебре понимается как алгебраическое сложение компонент векторов:
 . (1.2)
. (1.2)
Умножение вектора на число (скаляр) m есть получение вектора
 (1.3)
(1.3)
с новым абсолютным значением |m|A.
Скалярное произведение векторов
 обозначается
обозначается
 и определяется следующим образом:
и определяется следующим образом:
 , (1.4)
, (1.4)
где
 - угол между направлениями векторов. В
результате скалярного произведения
векторов образуется число. Как видно
из (1.4), значение скалярного произведения
может быть равным нулю при равных нулю
исходных векторах
(т.е. векторах с ненулевыми значениями
A и B),
либо при нулевых значениях
- угол между направлениями векторов. В
результате скалярного произведения
векторов образуется число. Как видно
из (1.4), значение скалярного произведения
может быть равным нулю при равных нулю
исходных векторах
(т.е. векторах с ненулевыми значениями
A и B),
либо при нулевых значениях
 .
В последнем случае эти векторы называются
ортогональными: они направлены под
прямым углом друг к другу.
.
В последнем случае эти векторы называются
ортогональными: они направлены под
прямым углом друг к другу.
Векторное произведение векторов
,
обозначаемое
 есть
есть
 , (1.5)
, (1.5)
где
 -
единичный вектор, направленный по
нормали к плоскости векторов
,
причем так, что
-
единичный вектор, направленный по
нормали к плоскости векторов
,
причем так, что
 образуют
«правую тройку»
векторов: если смотреть вдоль
,
то кратчайшее
угловое расстояние между векторами
,
обозначенное
φ, будет соответствовать движению
от
образуют
«правую тройку»
векторов: если смотреть вдоль
,
то кратчайшее
угловое расстояние между векторами
,
обозначенное
φ, будет соответствовать движению
от
 по часовой стрелке.
Удобно записывать векторное произведение
в форме следующего определителя:
по часовой стрелке.
Удобно записывать векторное произведение
в форме следующего определителя:
 (1.5a)
(1.5a)
раскрытие которого приводит к указанному результату. Векторное произведение некоммутативно, т.е. сомножители нельзя переставлять местами, имея в виду сохранение результата. А именно:
 . (1.6)
. (1.6)
Под векторно-скалярным
(смешанным) произведением векторов
 понимается скаляр
понимается скаляр
 ;
при этом
;
при этом
 , (1.7).
, (1.7).
т. е. важен циклический
порядок следования перемножаемых
векторов
 ,
при сохранении которого безразлично,
какие два вектора из трёх образуют
векторное произведение. На основании
(1.4) и (1.5) легко установить, что
,
при сохранении которого безразлично,
какие два вектора из трёх образуют
векторное произведение. На основании
(1.4) и (1.5) легко установить, что
 (1.8)
(1.8)
Далее, запишем формулу двойного векторного произведения:
 (1.9)
(1.9)
1.2. Линейное преобразование векторов. Вернёмся к вопросу об умножении вектора на скаляр. Согласно (1.3), равенство векторов
 (1.10)
(1.10)
равносильно трем скалярным равенствам:
 , (1.10а)
, (1.10а)
Если m
- положительное
число, то векторы
направлены
одинаково, а при отрицательном m
- противоположно («параллельно» и
«антипараллельно»); говорят, что такие
векторы
коллинеарны. Мы
имеем здесь дело с частным видом линейного
преобразования набора компонент
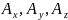 в аналогичный набор
в аналогичный набор
 ;
заметим, что эти совокупности компонент,
вполне определяющие векторы
,
мы также можем называть векторами.
;
заметим, что эти совокупности компонент,
вполне определяющие векторы
,
мы также можем называть векторами.
В общем случае под
однородным
линейным преобразованием
рассматриваемых
векторов понимают сопоставление
вектору
нового вектора
 ,
компоненты которого определяются по
формулам:
,
компоненты которого определяются по
формулам:
 , (1.11)
, (1.11)
где тхх, тху,..., тzу, тzz - некоторые числа. Векторы , компоненты которых связаны соотношениями (1.11), уже не коллинеарны; следовательно, записанное преобразование определяет не только изменение абсолютного значения («растяжение» или «сжатие») вектора, но и некоторый его поворот.
Остановимся на формальном описании преобразования (1.11). С точки зрения линейной алгебры, таблица чисел
 (1.12)
(1.12)
образует матрицу,
а равенства
(1.11)
выражают
операцию умножения
матрицы
 на вектор-столбец (
),
приводящую к вектору-столбцу (Вх,
Ву, Bz).
В частности, в (1.10а) мы имеем случай,
когда
на вектор-столбец (
),
приводящую к вектору-столбцу (Вх,
Ву, Bz).
В частности, в (1.10а) мы имеем случай,
когда
 ,
где
,
где
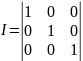 (1.13)
(1.13)
так называемая единичная матрица.
Вместо символа матрицы
введём иной символ
 и запишем равенства (1.11) в следующей
сокращённой форме:
и запишем равенства (1.11) в следующей
сокращённой форме:
 (1.14)
(1.14)
Умножение на здесь понимается как выполнение операций над компонентами вектора , содержащимися в. (1.11). Соотношение (1.14) есть обобщение равенства векторной алгебры (1.10), в котором роль множителя вместо скаляpa m играет объект более сложного характера , называемый тензором. В частности, единичной матрице I соответствует также обозначаемый единичный тензор I.
Тензор выступает как оператор, который, действуя на вектор , преобразует его в другой вектор .
1.3. Радиус-вектор.
Рассмотрим важный пример вектора,
зависящего от точки пространства, в
которой он рассматривается, т. е. пример
векторной функции. Это радиус-вектор
 ,
,
 , (1.15)
, (1.15)
который представляет собой направленный отрезок, соединяющий начало координат О (0, 0, 0) с некоторой «текущей» точкой М(х, у, z.). Длина радиус-вектора r = ОМ (его абсолютное значение) есть скалярная функция
 . (1.15а)
. (1.15а)
Очевидно, отрезок, соединяющий две точки Р(х', у', z') и М(х, у, z), изображается разностью их радиус-векторов:
 . (1.16)
. (1.16)
Абсолютное значение этого вектора выражает расстояние между точками Р и М:
 (1.16a)
(1.16a)
