1 сем / экз

Экзаменационные вопросы по курсу «Основные процессы и аппараты химической технологии»

Раздел 1. Основы гидравлики и гидравлические машины

Вопросы I:

1. Выведите уравнение неразрывности (сплошности) потока. Какой вид имеет это уравнение при стационарном течении несжимаемой жидкости?

Неразрывность (сплошность) потока означает, что в нем не образуются разрывы и пустоты

2.Что называют идеальной жидкостью? Выведите дифференциальные уравнения Эйлера движения идеальной жидкости.

3. Интегрированием соответствующих дифференциальных уравнений получите уравнение Бернулли течения идеальной жидкости.

4.Используя интеграл (уравнение) Бернулли для элементарной струйки, получите «уравнение Бернулли» для целого потока реальной жидкости. Каков физический смысл корректива кинетической энергии потока, и каковы его средние численные значения при различных гидродинамических режимах?

5.Выведите дифференциальные уравнения Навье - Стокса для случая одномерного течения жидкости. Каков физический смысл слагаемых этого уравнения?

В потоке реальной жидкости будут действовать как нормальные, так и касательные напряжения.

Рассмотрим сначала идеализированный случай однонаправленного движения несжимаемой вязкой жидкости, в котором все векторы скорости имеют одинаковые направления.

Выделим в потоке жидкости двигающейся параллельно оси z элементарный

параллелепипед, грани которого ориентированы по осям координат (Рис.2.1).

Будем считать, что вектор скорости vz уменьшается вдоль осей x и y . С учетом условия однонаправленности имеем

Ivx = vy = 0

Определим проекции внешних сил на ось z, действующих на элементарный объѐм.

Сила давления: PdI xdy − (p + ∂∂Px dz)d xdy = − ∂∂Pz d xdydz

Сила тяжести: I−ρgd xdydz

Сила трения, возникающая при изменении вектора скорости по оси x:

Iτsdzdy − (τs + ∂∂τxs d x)dzdy = − ∂∂τxs d xdydz

Сила трения при изменении вектора скорости по оси y

Iτsdzd x − (τs + ∂∂τys dy)dzd x = − ∂∂τys d xdydz

При равенстве скоростей Ix и Iy нулю касательные напряжения, действующие по оси z, при изменении скорости Iz по осям x и y выражаются по закону внутреннего трения Ньютона.

При изменении Iz по оси x: Iτs = τxz = − μ ∂vz

∂x

∂vz

равна I∂t ( индивидуальная производная равна частной).

В соответствии с основным принципом динамики получим уравнение баланса сил, действующих по оси z

Сократив на величину элементарного объема IdV = d xdydz , получим уравнение баланса сил, отнесенных к единице объема

Полученное уравнение выражает одновременно как баланс сил, так и баланс количества движения (импульса), так как левая часть уравнения (2.2) (произведение ускорения на массу единицы объѐма) равна скорости изменения импульса в единице объѐма, а правая часть этого уравнения равна потоку импульса, входящего в единицу объѐма, за счѐт действия внешних сил.

В общем случае, когда вектор скорости направлен произвольно, уравнения движения несжимаемой вязкой ньютоновской жидкости (баланса сил) в проекциях на оси координат имеют вид

Совместное решение уравнения (2.4) и уравнения неразрывности (1.14) позволяет получить поле скоростей и давлений в движущейся несжимаемой ньютоновской жидкости. Точные аналитические решения этой системы в силу еѐ нелинейности удаѐтся найти только для небольшого числа простых симметричных течений.

При Iμ = 0, уравнение Навье-Стокса переходит в уравнение Эйлера.

6.Получите формулу Стокса, описывающую распределение скоростей жидкости по сечению круглого канала. При ответе можно воспользоваться выражением оператора

7.Назовите гидродинамические режимы течения вязкой жидкости в прямом цилиндрическом канале. Какому режиму соответствует уравнение Iυi = 4μpL (r02 − r12) ),

описывающее распределение локальных скоростей по сечению канала? Используя это уравнение, получите в явном виде зависимость коэффициента Дарси (коэффициента трения) от числа Рейнольдса при соответствующем режиме течения.

Режимы течения:

•Ламинарный - движение слоев жидкости паралельными струйками, не смешивающихся друг с другом, скорость каждой их них постоянна и направлена вдоль общего течения

•Турбулентный -движение в жидкости носит хаотисный характер, слои постоянно перемешиваются. Частицы перемештваются с различными скоростями по неопределенно искривленным траекториям, в то время как масса жидкости движется в одном направлении.

Для горизонтальной трубы пост сечения : ∆p=p1-p2=∆pтр

64

Iλ = Re - кофицент трения Дарси

8.Решением соответствующих дифференциальных уравнений получите выражение, описывающее распределение скоростей по толщине плёнки жидкости, ламинарно стекающей по вертикальной твёрдой поверхности.

Пусть жидкость ламинарно стекает по вертикальной поверхности в виде тонкой пленки при установившемся течении.

Ось у направлена в сторону уменьшения скорости перпендикулярно стенке, ось z- в сторону спекания пленки,ось х- вдоль поверности пленки(по ширене)

При ламинарном режиме частицы перемещаются только вдоль оси z Iνx , νy = 0

Вопросы 2:

1.Сформулируйте закон Ньютона внутреннего трения и запишите соответствующую формулу для случая одномерного течения жидкости. Какова взаимосвязь между коэффициентами динамической и кинематической вязкости; в каких единицах системы СИ измеряются эти коэффициенты?

 По закону Ньютона сила внутреннего трения, т. е. сила, проявляющаяся при перемещении одного слоя жидкости относительно другого, прямо пропорциональна относительной скорости перемещения и величине поверхности соприкосновения этих слоев. Она зависит от свойств жидкости и не зависит от давления.

2.Что такое гидравлический радиус и эквивалентный диаметр. Приведите пример (по Вашему выбору) расчёта эквивалентного диаметра в канале некруглого поперечного сечения.

3.Опишите последовательность расчёта диаметра аппарата или трубопровода. Укажите примерные численные значения скоростей капельных жидкостей, газов и паров в трубопроводах. Поясните, чем обусловлены именно такие значения скоростей?

4.Запишите уравнение Бернулли течения идеальной жидкости. Каков физический смысл слагаемых этого уравнения?

Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила - сила тяжести.

Выбреем два живых сечения(Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения) , 1-1 в начале рассматриваемого участка, 2-2 - в конце.

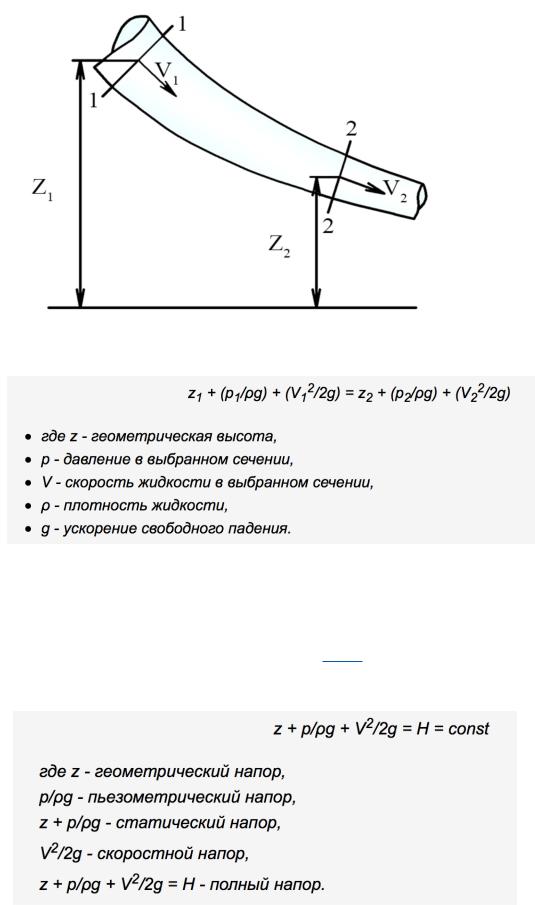
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении

Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор - величина постоянная.