7. На кінець добавляємо букву «а», щоб завершити побудову дерева, а потім позначимо кожну ліву гілку «0», а кожну праву «1».

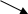0 1

28

0 1

A 0 1 18 0 1

10 10 8

0 1 0 1

<SPACE> 4 N 4

6 4 0 1

L M Р 2

2 2 2

С .

1 1

Таблиця 3.9. Коди Хафмана для символів паліндрому:

Значення	Код Хафмана	Довжина коду	Частота використання	Використання бітів
A C L M N P <SPACE> .	0 11110 1010 1011 110 1110 100 11111	1 5 4 4 3 4 3 5	10 1 2 2 4 2 6 1	10 5 8 8 12 8 18 5

28 Всього 74

Якби застосовувати коди постійної довжини , потрібно було б 3 біти на символ, і загальна кількість бітів склала б:

30+3+6+6+12+6+18+3=28*3=84 символів.

Як видно з Таблиці 3.9 жоден із кодів символів не є префіксом до будь-якого іншого коду. Наприклад, букві N присвоєно код 110, і ні один із кодів в таблиці не розпочинається із бітового рядка 110. Це дуже важлива особливість, без якої неможливо було б декодувати рядок.

Дискретне косинусне перетворення.

(Discrete Cosine Transform – DCT ) – ключовий метод стиснення у формі JPEG

Перетворення - це операція, що відображає елементи однієї величини на елементи іншої множини.(Приклад – відображення букв на цілі числа за допомогою кодів ASCII).

Перетворення DCT відноситься до обернених перетворень, для яких вихідні коефіцієнти (output coefficients) можуть використовуватись для відновлення початкових вхідних початкових вхідних даних. Перетворення обернене DCT, називається оберненим дискретним косинусним перетворенням (Inverse Discrete Cosine Trsnsform - IDCT). Перетворення DCT часто називають прямим DCT (Forward DCT - FDCT).

Перетворення DCT перетворює набір вхідних значень у набір коефіцієнтів косинусних функцій із частотами, що зростають. Кожне вихідних значень перетворюється у суму косинусів.

У форматі JPEG перетворення DCT та IDCT завжди виконується у двох вимірах над даними, що згруповані в блоки розміром 8x8.

Перетворення DCT у одному вимірі.

Одномірне перетворення DCT масиву V із чисел N в масив T із N чисел визначається як:

, де 3.1

, k=0

Для оберненого процесу використовується одномірне перетворення IDCT. Воно визначається:

3.2

В основу покладена функція . Це циклічна функція, так що при зростанні Х значення функції починає зростати кожен раз, коли Х досягає значення, яке кратне 2π. Частота, з якою повторюється значення косинусної функції можна змінювати за рахунок виключення у функцію константи n.

Чим більше значення N,тим частіше повторюється значення косинусної функції. При множенні Cos-функції на друге значення можна налаштовувати амплітуду косинусоїду. Оскільки значення Cos лежить в діапазоні від -1 до +1, для функції y=A*cos(xnΠ) постіне значення А є амплітудою косинусоїди. Якщо виконати підстановку та у рівняння 3.2, можна побачити, що IDCT є сумою косинусних функцій, частота яких зростає разом з порядковим номером косинусної функції, а коефіцієнтами DCT визначають амплітуди відповідних косинусних функцій у загальній сумі.

Приклад.

n	0	1	2	3	4	5	6	7
Вхід	128	88	40	0	0	40	88	128
DCT	181	0.0	136.0	0.0	0.0	0.0	4.6	.0

Рис. 3.10. Дискретні значення, їх одномірні DCT та IDCT – коефіцієнти для n=1.

В режимах JPEG, що використовують для вхідних даних 8 бітів, вхідні значення можуть змінюватись в діапазоні від 0 до 255. Стандарт JPEG вимагає, щоб до виконання розрахунків DCT із всіх вхідних значень віднімалось 128, щоб діапазон значень знаходився від -128 до +127. Це призводить до зменшення значень першого коефіцієнту DCT, але не впливає на значення всіх інших коефіцієнтів. Після виконання IDCT необхідно добавити 128, щоб повернути результат назад у вірний діапазон.

Якщо перетворення DCT і IDCT виконувати послідовно і з абсолютною точністю, результат завжди буде співпадати із вхідними даними. Але в комп’ютері під час створення JPEG всі значення DCT заокруглюються до цілих чисел, а це вносить (хоч і не велику) помилку в процес відновлення даних.

Відкидаючи коефіцієнти вищого порядку (вони вносять у зображення меншу частину інформації) можна добиватись кращого стиснення, але за рахунок якості. Краще піддаються такій процедурі фотографії (нема різних перепадів кольорів, гірше – картини. Для рисунків краще підходять формат PNG).

Квантування.

Після розрахунку DCT наступний крок включає пошук та відкидання коефіцієнтів, вклад яких у формування зображення мінімальний. Для вирішення цієї задачі стандарт JPEG визначає простий механізм квантування (quantiration).

Щоб виконати квантування коефіцієнтів DC T, досить просто поділити їх на значення кванту, та заокруглити до ближнього цілого.