
- •Общая физика
- •§ 1. Кинематика материальной точки и поступательного движения твердого тела
- •II закон Ньютона. Ускорение, приобретаемое материальной точкой (телом) пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
- •III закон Ньютона. Силы, с которыми действуют друг на друга тела, равны по модулю и противоположены по направлению.
- •2.2. Закон сохранения импульса (количества движения)
- •2.3. Энергия, работа, мощность
- •2.4. Закон сохранения и превращения энергии
- •2.5 Тяготение
- •2.6. Механика вращательного движения
- •Момент инерции, момент силы, момент импульса.
- •И вращательном движениях
- •2.7.Колебания и волны Механические колебания, математический маятник
- •2.8. Границы применимости законов классической механики и элементы специальной теории относительности
- •§ 1. Параметры термодинамических систем (параметры состояния)
- •§ 2. Законы идеальных газов
- •§ 3. Уравнение состояния реальных газов
- •Уравнение ван-дер-ваальса или уравнение состояния реальных газов
- •§4. Основы термодинамики.
- •Кинетической теории идеальных газов
- •Наиболее вероятная (максимальная)
- •§1. Электрическое поле
- •§1.1. Силовые характеристики электрического поля
- •§1. 2. Энергетические характеристики электрического поля
- •§1.3. Диполь
- •§1.4. Проводники в электрическом поле
- •§1.5. Диэлектрики в электрическом поле
- •§1.6. Электроемкость
- •§1.7. Конденсаторы
- •§1.8. Энергия электростатического поля
- •§2.1. Электродвижущая сила (эдс) (e ) источника
- •§2.2. Закон Ома для постоянного тока
- •§2.3. Закон Джоуля-Ленца
- •§2.4. Правила Кирхгофа (1847г.)
- •§2.5. Зонная теория
- •Гл. 3 электромагнетизм
- •§3.1. Характеристики магнитного поля
- •И мп на оси кругового тока.
- •§3.2. Вещество в магнитном поле
- •§3.3. Рамка с током в магнитном поле (Применения закона Ампера)
- •§3.4. Сила Лоренца
- •§3.5. Движение заряженных частиц в электрическом поле
- •§3.6. Движение заряженных частиц в магнитном поле
- •§ 3.7. Электромагнитная индукция: Закон Фарадея − Ленца
- •§3.8. Закон Ома для полной цепи
- •§3.9. Индуктивность, самоиндукция, взаимная индукция
- •1 Гн индуктивность такого контура, магнитный поток самоиндукции которого при токе 1 а равен 1 Вб.
- •§3.10. Энергия магнитного поля
- •§4.1. Полное сопротивление цепи при переменном токе.
- •§4.2. Резонанс
- •Шкала электромагнитных волн
- •§1.1. Поглощение света (Закон бугера)
- •§1.2. Законы геометрической оптики
- •§1.3. Формула призмы
- •§1.4. Линзы
- •Характер изображения собирающей линзы
- •§1.5. Аберрации или погрешности оптических систем
- •§2. Волновая оптика
- •§2.1. Интерференция света
- •§2.2. Дифракция света
- •РешеткаУсловияУсловия§2.3. Дисперсия света и спектральный анализ
- •§ 2.4. Поляризация света
- •Объяснение законов отражения и преломления с точки зрения волновой теории
- •§1. Тепловое излучение
- •Закон Стефана - Больцмана. Полная (по всему спектру) излучательная способность абсолютного черного тела прямо пропорциональна четвертой степени его абсолютной (термодинамической) температуре т:
- •§ 2. Фотоэффект
- •§ 3. Строение вещества
- •§ 3.1. Модели атома Резерфорда
- •§ 3.2. Постулаты Бора
- •§ 3.3. Правила отбора Паули, квантовые числа и таблица Менделеева
- •Периодическая система элементов Менделеева и распределение электронов по подоболочкам
- •§ 3.4. Радиоактивность
- •Закон радиоактивного распада
- •§ 3.5. Физика атомного ядра
- •§ 3.6. Элементарные и фундаментальные частицы
- •Классификация частиц
- •§3.7. Волновые свойства микрочастиц
- •§3.8. Соотношение неопределенности Гейзенберга
- •§3.9. Основы квантовой механики.
- •Основная литература
- •Вспомогательная литература
- •Контрольные вопросы по физике Трофимова т.И., Курс физики, «Высшая школа»,2000г.
- •Применение первого начала термодинамики к термодинамическим изопроцессам
- •Приложение к теме «Оптика» основные фотометрические величины и их единицы
2.4. Закон сохранения и превращения энергии
Многовековые опыты показывают, что какие бы превращения энергии ни происходили в изолированной системе, полная энергия изолированной системы остается постоянной. При этом, будучи не создаваемой и неуничтожаемой, энергия может превращаться из одних видов в другие (закон сохранения и превращения энергии).
Закон сохранения и превращения энергии, как все фундаментальные, всеобщие законы природы, не имеет общего теоретического доказательства и может быть теоретически выведен только для частных случаев.
Выведем его для механической системы, состоящий из n материальных точек. Второй закон Ньютона для материальных точек системы:
![]() ,
,
где
![]() − равнодействующие внутренних
консервативных сил,
− равнодействующие внутренних
консервативных сил,
![]() − равнодействующие
внешних консервативных сил,
− равнодействующие
внешних консервативных сил,
![]() − равнодействующие
внешних неконсервативных сил.
− равнодействующие
внешних неконсервативных сил.
Умножая обе части
уравнения на![]() и учитывая, что
и учитывая, что
![]() ,
получаем
,
получаем
![]()
![]() ,
,
где![]() −приращение
кинетической энергии системы,
−приращение
кинетической энергии системы,
![]() −
элементарная
работа внутренних и внешних консервативных
сил, который со знаком минус равна
элементарному приращению потенциальной
энергии системы,
−
элементарная
работа внутренних и внешних консервативных
сил, который со знаком минус равна
элементарному приращению потенциальной
энергии системы,
![]() −
работа внешних
неконсервативных сил, действующих на
систему.
−
работа внешних
неконсервативных сил, действующих на
систему.
![]()
Интегрируя из
состоянии 1 → 2, получим
![]() .
.
Изменение полной механической энергии системы при переходе из одного состояния в другое, равно работе, совершенной при этом внешними неконсервативными силами.
Если сумма внешних
неконсервативных сил равна нулю, то
![]() .
.
Или
![]() 5
5
Полная механическая энергия замкнутой системы тел, в которой действуют только консервативные силы, сохраняется, не изменяется со временем.
Обобщая, В замкнутой системе общее количество энергии всех видов остается строго постоянной независимо от того, какие процессы происходят в этой системе.
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этой формулировке отражены основные свойства энергии – количественная неизменность и качественная изменчивость. Закон сохранения энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени, то есть они не зависят от выбора начала отсчета времени. Если в любые два момента времени замкнутую систему поставить в совершенно одинаковых условиях, то, начиная с этих моментов времени, все процессы в системе будут протекать совершенно одинаково. Например, при свободном падении тела в поле сил гравитации его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, в какой момент времени тело начало падать.
Закон сохранения и превращения энергии для неизолированной системы: Изменение энергии неизолированной системы равно работе, совершаемой системой.
ΔЕ=−А
Если работа совершается внутренними силами самой системы, то A>0 и энергия системы убывает. Если же работа совершается внешними силами над системой, то A<0 и энергия системы возрастает.
Закон сохранения и превращения энергии - фундаментальный закон природы, не имеющий исключений, выполняется и в макромире и в микромире.
Неизменность полной механической энергии замкнутой системы (Е= Wк+Wр =const) приводит к тому, что мы иногда наглядно наблюдаем превращение кинетической энергии в потенциальную и наоборот (например, при колебании математического маятника).
Примеры
Абсолютные упругие и неупругие соударения
Абсолютное упругое соударение (удар) − столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Естественно это идеализированный случай − физическая модель. После соударения тела отделяются друг от друга и движутся самостоятельно, а кинетическая энергия перераспределяется между ними.
В данном случае соблюдаются законы сохранения импульса и механической энергии:
![]() ,
,
![]() ,
,
где m1,
m2 − массы
тел,
,
![]() − скорости первого тела до и после
соударения,
,
− скорости первого тела до и после
соударения,
,
![]() − скорости второго тела до и после
соударения.
− скорости второго тела до и после
соударения.
![]()
 ,
,
![]() ,
,
![]()
При прямого, центрального удара находим:
![]()
![]()
Абсолютное неупругое соударение − столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При таких столкновениях часть первоначальной кинетической энергии превращается в энергию деформации, поэтому в данном случае не соблюдается закон сохранения механической энергии.
![]() ,
,
![]() ,
,
где
![]() −
скорость движения шаров после соударения.
−
скорость движения шаров после соударения.
«Потеря» кинетической энергии
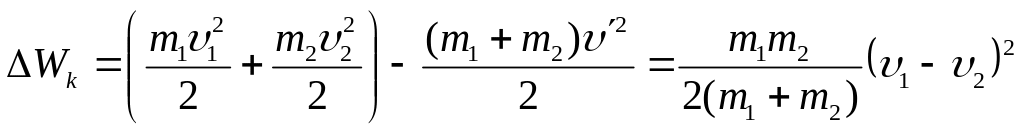 .
.
Если
=0,
то
![]() ,
,
![]() .
.
Когда m2
>> m1,
(масса неподвижного тела очень большая),
то
![]() и почти вся кинетическая энергия первого
тела при ударе переходит в другие формы
энергии. Для значительной деформации
наковальня должна быть массивнее
молотка. Наоборот, при забывании гвоздей
в стенку масса молотка должна быть
побольше (m1>>m2),
тогда
и почти вся кинетическая энергия первого
тела при ударе переходит в другие формы
энергии. Для значительной деформации
наковальня должна быть массивнее
молотка. Наоборот, при забывании гвоздей
в стенку масса молотка должна быть
побольше (m1>>m2),
тогда
![]() и практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
и практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
