§3.7. Волновые свойства микрочастиц

Из универсального закона взаимосвязи массы и энергии вытекает, что энергия Е и масса m_ф фотона связаны соотношением: Е= m_ф^. с².

Так как фотон обладает энергией E=hν, то его масса m_ф = .

Поставив это выражения массы в формулу импульса фотона, получаем, что импульс фотона , отсюда .

Луи де Брайль в 1924 году пришел к выводу, что корпускулярно-волновой дуализм присущ не только излучению и световым фотонам, но и материальным частицам, то есть любая движущаяся частица вещества должна, как квант излучения – фотон, обладать и волновыми свойствами. Для длин волн микрочастиц, он предлагал выражение, аналогичное для фотона, т.е. любой частице, обладающей импульсом p=mυ, свойственна длина волны:

(формула де Бройля),

где - длина волны де Бройля, h=6,625^.10^-34 Дж^.с – постоянная Планка.

Предсказанные де Бройлем волновые свойства частиц впоследствии были обнаружены экспериментально при наблюдении дифракции электронов и других частиц на кристаллах (опыты Дэвиссона-Джермера в 1927г.). Более того, было доказано, что волновые свойства частиц не являются свойствами их коллектива, а присущи каждой частице в отдельности. Проходя через металлическую фольгу, и пучок электронов, и идущие друг за другом отдельные электроны, показывают схожую дифракционную картину.

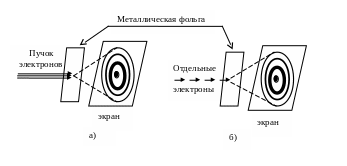
В связи с этим возникал вопрос; почему раньше в макромире не обнаружились волны де Бройля? Простые расчеты показывают, что, например, частице с m=1мг и υ=1м/с, соответствует волна де Бройля с =6^.10^-28м, которая невозможно обнаружить т.к. в природе не существуют периодические структуры с периодом 10^-28м. Для микрочастиц с маленькими массами и с большими скоростями, становится сравнима или больше решетки кристалла (10^-8см) и уже можно наблюдать их волновые свойства, например, дифракцию электрона на кристаллическую решетку. Поэтому можно считать (как это и делается в классической механике), что макроскопические тела не обладают волновыми свойствами.

Рассчитав по формуле де Бройля длину волны , соответствующую электронным лучам, используемым в электронном микроскопе (при скорости υ=1,4^.10⁸ м/с и массе электрона m=9,1^.10^-31кг), получаем ≈5^.10^-12 м. Эта длина электронной волны в электронном микроскопе приблизительно в 100 000 раз меньше средней длины волны видимого света (~5^.10^-7м). Этим и обусловлена большая разрешающая способность электронного микроскопа по сравнению с оптическим микроскопом. (Разрешающая способность оптического микроскопа ~3^.10^-7м, а у современных электронных микроскопов -5^.10^-10м, что позволяет в таких микроскопах рассматривать даже отдельные атомы и молекулы.)

Существование волн де Бройля позволяет истолковать корпускулярно - волновой дуализм света в более широком смысле: двойственная природа присуща не только свету, но всем микрочастицам! Микрообъекты существенно (качественно) отличаются от привычных для нас объектов макромира. Для частиц или тел макромира такая двойственная природа невозможно представить. Частица макромира занимает ограниченную область пространства и движется по определенной траектории (или покоится); волна же распределена в пространстве непрерывно и ее энергия передается всем точкам пространства. Сочетая в себе свойства частицы и волны, микротела «не ведут себя ни как волны, ни как частицы…». Отличие микрочастицы от волны заключается в том, что она всегда обнаруживается как неделимое целое (никто никогда не наблюдал, например, полэлектрона). В то же время волну можно разделить на части (например, направив световую волну на полупрозрачное зеркало) и воспринимать затем каждую часть в отдельности.

Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы ε и частотой ν волны де Бройля:

ε =h ν.

Это свидетельствует о том, что соотношение между энергией и частотой в этой формуле имеет характер универсального соотношения, справедливого как для фотонов, так и для любых других микрочастиц.

Делались попытки корпускульярно-волновой дуализм объяснить моделями, где частицы рассматривались как «узкие» волновые пакеты, «составленные» из волн де Бройля. Это позволило, как бы отойти от двойственности свойств частиц. Такая гипотеза соответствовала локализации частицы в данный момент времени в определенной ограниченной области пространства. Тем более, что скорость распространения центра такого пакета (групповая скорость) оказалась равной скорости частиц. Однако подобное представление частицы в виде волнового пакета (группы волн де Бройля) оказалось несостоятельным из-за сильной дисперсии волн де Бройля. Т.к. скорость волн де Бройля зависит от длины волны, дисперсия приводила к «быстрому расплыванию» (примерно за 10^-26с) волнового пакета или даже разделению его на несколько пакетов.

По словам академика Фока; «для атомного объекта (микрочастицы) существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна-частица. Всякое иное, более буквальное, понимание этого дуализма в виде какой-нибудь модели (классической) неправильно».