
- •Общая физика
- •§ 1. Кинематика материальной точки и поступательного движения твердого тела
- •II закон Ньютона. Ускорение, приобретаемое материальной точкой (телом) пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
- •III закон Ньютона. Силы, с которыми действуют друг на друга тела, равны по модулю и противоположены по направлению.
- •2.2. Закон сохранения импульса (количества движения)
- •2.3. Энергия, работа, мощность
- •2.4. Закон сохранения и превращения энергии
- •2.5 Тяготение
- •2.6. Механика вращательного движения
- •Момент инерции, момент силы, момент импульса.
- •И вращательном движениях
- •2.7.Колебания и волны Механические колебания, математический маятник
- •2.8. Границы применимости законов классической механики и элементы специальной теории относительности
- •§ 1. Параметры термодинамических систем (параметры состояния)
- •§ 2. Законы идеальных газов
- •§ 3. Уравнение состояния реальных газов
- •Уравнение ван-дер-ваальса или уравнение состояния реальных газов
- •§4. Основы термодинамики.
- •Кинетической теории идеальных газов
- •Наиболее вероятная (максимальная)
- •§1. Электрическое поле
- •§1.1. Силовые характеристики электрического поля
- •§1. 2. Энергетические характеристики электрического поля
- •§1.3. Диполь
- •§1.4. Проводники в электрическом поле
- •§1.5. Диэлектрики в электрическом поле
- •§1.6. Электроемкость
- •§1.7. Конденсаторы
- •§1.8. Энергия электростатического поля
- •§2.1. Электродвижущая сила (эдс) (e ) источника
- •§2.2. Закон Ома для постоянного тока
- •§2.3. Закон Джоуля-Ленца
- •§2.4. Правила Кирхгофа (1847г.)
- •§2.5. Зонная теория
- •Гл. 3 электромагнетизм
- •§3.1. Характеристики магнитного поля
- •И мп на оси кругового тока.
- •§3.2. Вещество в магнитном поле
- •§3.3. Рамка с током в магнитном поле (Применения закона Ампера)
- •§3.4. Сила Лоренца
- •§3.5. Движение заряженных частиц в электрическом поле
- •§3.6. Движение заряженных частиц в магнитном поле
- •§ 3.7. Электромагнитная индукция: Закон Фарадея − Ленца
- •§3.8. Закон Ома для полной цепи
- •§3.9. Индуктивность, самоиндукция, взаимная индукция
- •1 Гн индуктивность такого контура, магнитный поток самоиндукции которого при токе 1 а равен 1 Вб.
- •§3.10. Энергия магнитного поля
- •§4.1. Полное сопротивление цепи при переменном токе.
- •§4.2. Резонанс
- •Шкала электромагнитных волн
- •§1.1. Поглощение света (Закон бугера)
- •§1.2. Законы геометрической оптики
- •§1.3. Формула призмы
- •§1.4. Линзы
- •Характер изображения собирающей линзы
- •§1.5. Аберрации или погрешности оптических систем
- •§2. Волновая оптика
- •§2.1. Интерференция света
- •§2.2. Дифракция света
- •РешеткаУсловияУсловия§2.3. Дисперсия света и спектральный анализ
- •§ 2.4. Поляризация света
- •Объяснение законов отражения и преломления с точки зрения волновой теории
- •§1. Тепловое излучение
- •Закон Стефана - Больцмана. Полная (по всему спектру) излучательная способность абсолютного черного тела прямо пропорциональна четвертой степени его абсолютной (термодинамической) температуре т:
- •§ 2. Фотоэффект
- •§ 3. Строение вещества
- •§ 3.1. Модели атома Резерфорда
- •§ 3.2. Постулаты Бора
- •§ 3.3. Правила отбора Паули, квантовые числа и таблица Менделеева
- •Периодическая система элементов Менделеева и распределение электронов по подоболочкам
- •§ 3.4. Радиоактивность
- •Закон радиоактивного распада
- •§ 3.5. Физика атомного ядра
- •§ 3.6. Элементарные и фундаментальные частицы
- •Классификация частиц
- •§3.7. Волновые свойства микрочастиц
- •§3.8. Соотношение неопределенности Гейзенберга
- •§3.9. Основы квантовой механики.
- •Основная литература
- •Вспомогательная литература
- •Контрольные вопросы по физике Трофимова т.И., Курс физики, «Высшая школа»,2000г.
- •Применение первого начала термодинамики к термодинамическим изопроцессам
- •Приложение к теме «Оптика» основные фотометрические величины и их единицы
Характер изображения собирающей линзы
a |
b |
Характер изображения |
Оптическая система |
a=∞ |
b=f |
Точечное в фокусе |
- |
∞>а>2f |
f<b<2f |
Действительное, обратное, уменьшенное |
Глаз, фотоаппарат |
а=2f |
b=2f |
Действительное, обратное, равное предмету |
Переносная или оборачивающая линза |
2f>а>f |
2f<b<∞ |
Действительное, обратное, увеличенное |
Объектив микроскопа |
а=f |
b=∞ |
Параллельные лучи |
- |
a<f |
- |
Мнимое, прямое, увеличенное |
Окуляр, лупа |
Для рассеивающей линзы характер изображения не зависит от расстояния предмета от линзы: у них изображение всегда мнимое, прямое и уменьшенное.
Комбинации собирающих и рассеивающих линз (так называемые сложные объективы) применяются в оптических приборах, используемых для решения различных научных и технических задач. Оптическая сила сложного объектива представляет собой алгебраическую сумму оптических сил отдельных линз: D=±D1± D2 ±D3 ±…..
Этот принцип используется для коррекции зрения, когда роль одной линзы играет хрусталик глаза14, а роль другой – стекло очков или контактные линзы.
Угловое увеличение
Г
оптического прибора:
![]() ,
где α′ и
α − углы
зрения, под которыми виден предмет
соответственно через прибор и невооруженным
глазом. Для лупы
,
где α′ и
α − углы
зрения, под которыми виден предмет
соответственно через прибор и невооруженным
глазом. Для лупы
![]() ,
где L0
=25см расстояние
наилучшего зрения,
,
где L0
=25см расстояние
наилучшего зрения,
![]() ,
т.к. глаз располагают вблизи заднего
фокуса лупы.
,
т.к. глаз располагают вблизи заднего
фокуса лупы.
Тогда Г=![]()
Увеличение лупы обратно пропорционально ее фокусному расстоянию и показывает, во сколько раз увеличивается линейный размер изображения на сетчатке за счет применения лупы.
Л инейное
увеличение луп не так уж велико (меньше,
чем 20 раз), поэтому, используя комбинацию
из двух (обычно сложных) линз, при помощи
микроскопа можно получить гораздо
больше увеличение (~1000 раз). Для начертания
принципиальной схемы микроскопа надо
использовать вышеуказанную таблицу и
учитывать, что изображение через вторую
линзу (окуляр)
можно получить только от действительного
изображения первой линзы (объектива).
инейное
увеличение луп не так уж велико (меньше,
чем 20 раз), поэтому, используя комбинацию
из двух (обычно сложных) линз, при помощи
микроскопа можно получить гораздо
больше увеличение (~1000 раз). Для начертания
принципиальной схемы микроскопа надо
использовать вышеуказанную таблицу и
учитывать, что изображение через вторую
линзу (окуляр)
можно получить только от действительного
изображения первой линзы (объектива).
Расстояние между внутренними фокусами объектива и окуляра называется оптической длиной тубуса (ℓ≈160мм). Увеличение Г микроскопа: Г=Гоб∙Гок. Как лупа Гок=L0/fок , а Гоб=ℓ/fоб , т.к. ℓ>>fоб ,
Г
![]()
Увеличение микроскопа прямо пропорционально оптической длине ℓ тубуса и обратно пропорционально произведению фокусных расстояний объектива и окуляра. Гмикроскоп ≈56÷1350 (максимально ~2000), но обычно используются 1000÷1200 – кратное увеличение.
§1.5. Аберрации или погрешности оптических систем

Х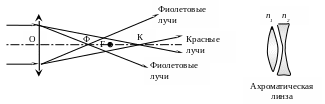 роматическая
аберрация
возникает из-за того, что коэффициент
преломления n=n(λ)
зависит от длины волны света (явление
дисперсии
− отсутствует у зеркал). Собирающая
линза приближает к оптической оси
сильнее фиолетовые лучи, чем красные,
а рассеивающая линза, наоборот, приближает
к оптической оси сильнее красные лучи.
Благодаря этому можно создать оптическую
систему (ахроматическая
линза), не
имеющую хроматической аберрации.
Комбинация двух линз с разными п
уменьшает хроматическую аберрацию
много (~16) раз. Так как разные сорта стекол
обладают различной дисперсией, то,
комбинируя собирающие и рассеивающие
линзы из различных стекол, можно
совместить фокусы двух (ахроматы)
и трех (апохроматы)
различных цветов, устранив тем самым
хроматическую аберрацию. Системы,
исправленные на сферическую и хроматическую
аберрации, называются аплантами.
роматическая
аберрация
возникает из-за того, что коэффициент
преломления n=n(λ)
зависит от длины волны света (явление
дисперсии
− отсутствует у зеркал). Собирающая
линза приближает к оптической оси
сильнее фиолетовые лучи, чем красные,
а рассеивающая линза, наоборот, приближает
к оптической оси сильнее красные лучи.
Благодаря этому можно создать оптическую
систему (ахроматическая
линза), не
имеющую хроматической аберрации.
Комбинация двух линз с разными п
уменьшает хроматическую аберрацию
много (~16) раз. Так как разные сорта стекол
обладают различной дисперсией, то,
комбинируя собирающие и рассеивающие
линзы из различных стекол, можно
совместить фокусы двух (ахроматы)
и трех (апохроматы)
различных цветов, устранив тем самым
хроматическую аберрацию. Системы,
исправленные на сферическую и хроматическую
аберрации, называются аплантами.
Хроматическую аберрацию можно уменьшить, увеличивая фокусное расстояние линзы, хотя это не всегда технически выполнимо. Например, при диаметре линзы D=0,5м, F=2,8м, при D=1м, F=112м (технически невыполним).
Сферическая аберрация обусловлена сферичностью преломляющих поверхностей линз (отсутствует у параболических зеркал). При большом диаметре линзы часть лучей перестанут быть параксиальными, в результате чего изображения получаются размытыми (сферическая аберрация).
У
 собирающей линзы лучи, падающие на ее
края, собираются ближе, чем лучи, падающие
на ее центральную часть (δ<0);
у рассеивающей линзы наблюдается
обратное явление (δ>0).
Благодаря этому можно создать оптическую
систему (анастигматы)
из соответствующим образом подобранных
собирающей и рассеивающей линз, у которой
сферическая аберрация почти полностью
отсутствует. Применяя диафрагмы
(ограничиваясь параксиальными лучами),
можно уменьшить сферическую аберрацию,
однако пи этом уменьшается светосила
линзы.
собирающей линзы лучи, падающие на ее
края, собираются ближе, чем лучи, падающие
на ее центральную часть (δ<0);
у рассеивающей линзы наблюдается
обратное явление (δ>0).
Благодаря этому можно создать оптическую
систему (анастигматы)
из соответствующим образом подобранных
собирающей и рассеивающей линз, у которой
сферическая аберрация почти полностью
отсутствует. Применяя диафрагмы
(ограничиваясь параксиальными лучами),
можно уменьшить сферическую аберрацию,
однако пи этом уменьшается светосила
линзы.
В 1941г. Д.Д. Максутовым была создана безаберрационная оптическая система (менисковый телеобъектив), состоящая из вогнутого сферического зеркала и выпукло-вогнутой сферической линзы (мениска). Зеркало и мениск в отдельности обладают большими аберрациями (сферическими), имеющими противоположные знаки; в менисковом телеобъективе эти аберрации полностью компенсируются.
Сферическая аберрация является частным случаем астигматизма.
Астигматизм − погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка. Устраняется при помощи сложных линз (широкоугольные объективы до 700). Астигматизм исправляется подбором радиусов кривизны преломляющих поверхностей и их фокусных расстояний. Системы, исправленные на сферическую и хроматическую аберрации и астигматизм, называются анастигматами.

Просветленная оптика
Для уменьшении
отражения на границах линз, их покрывают
пленкой фторида
магния MgF2
с
![]() и с такой толщины, чтобы световые волны
1
и 2
гасили друг друга (имели противоположные
фазы). Поглощение в стекле линз возрастает
в ультрафиолетовой
и инфракрасной
части спектра, поэтому для этих лучей
используют кварц
или зеркало.
и с такой толщины, чтобы световые волны
1
и 2
гасили друг друга (имели противоположные
фазы). Поглощение в стекле линз возрастает
в ультрафиолетовой
и инфракрасной
части спектра, поэтому для этих лучей
используют кварц
или зеркало.

Примеры по геометрической оптике:




Приложение 1
Прохождение света через плоскопараллельную пластину
Пластина смещает луч света параллельно самому себе на расстояние ℓ

Из ΔABC → BC=AB.sin(α─β)
Из ΔADB → AB=d/cosβ
BC=ℓ=d.sin(α─β)/cosβ
Или как f(d,α,n)

Приложение 2
Формула тонкой линзы (по Физика для поступающих, Бутиков Е.И. и др.,М., «Наука», 1978г.)
И з
принципа Ферма следует, что оптические
длины всех лучей, выходящих из источника
А
и собирающихся в точке В,
являющейся его изображением, одинаковы.
з
принципа Ферма следует, что оптические
длины всех лучей, выходящих из источника
А
и собирающихся в точке В,
являющейся его изображением, одинаковы.
a+n(c+d)+b=AC+CB
Из теоремы Пифагора:
![]() =
=
=
![]()
Т.к.
h<<d,
то используя
![]() при x<<1
при x<<1
![]()
Аналогично
![]() ,
,
поэтому
![]() →
→
![]() →
→
![]() ,
т.к. a>>c,
b>>d
,
т.к. a>>c,
b>>d
также
c=![]() ,
и аналогично
,
и аналогично
![]() .
.
Окончательно
![]()
Приложение 3
Формула тонкой линзы (по Трофимовой)
Д ве
световые лучи, выходящие из точки А
(луч АОВ
и луч, проходящий через край линзы, АСВ),
должны доходить до точки В,
одновременно. Время прохождения света
вдоль АОВ
ве
световые лучи, выходящие из точки А
(луч АОВ
и луч, проходящий через край линзы, АСВ),
должны доходить до точки В,
одновременно. Время прохождения света
вдоль АОВ
![]() ,
где N=n/n1
-относительный показатель преломления
(n
и n1
- соответственно абсолютные показатели
преломления линзы и окружающей среды).
Время прохождения света вдоль АСВ
равно
,
где N=n/n1
-относительный показатель преломления
(n
и n1
- соответственно абсолютные показатели
преломления линзы и окружающей среды).
Время прохождения света вдоль АСВ
равно
![]() .
Так как t1=t2
, то
.
Так как t1=t2
, то
![]() .
.
Рассматривается
параксиальные
(приосевые) лучи,
т. к. только они, исходящие из точки A,
пересекают оптическую ось в одной и той
же точке В.
тогда h<<(a+e),
h<<(b+d)
и
 .
Аналогично
.
Аналогично
![]() .Подставив
эти выражения в
.Подставив
эти выражения в
![]() .
.
Для тонкой линзы
e<<a
и d<<b,
поэтому
![]() .
Учитывая, что
.
Учитывая, что
 и соответственно
и соответственно
![]() ,
получим
,
получим
![]()
Приложение 4
Формула тонкой линзы (по Грабовскому)

Построим плоскости, касательные к поверхностям линзы в точках M и N (т.е. в местах падения луча на линзу и выхода его из линзы), и проведем в эти точки радиусы R1 и R2 кривизны линзы. Тогда луч AMNA1 можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α1, β1 и толщины линзы, можно написать следующие приближенные равенства:
h1≈h2,
|AD|≈a,|A1D1|≈b,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где h1 - высота (над оптической осью) точки M падения луча на линзу, h2 - высота точки N выхода луча из линзы, a и b - соответственно расстояния от источника света A и от его изображения A1 до оптического центра линзы.
Из треугольников AHA1 и BEB1 следует, что δ=α+α1 и θ=β+β1.
Тогда, принимая во внимание значения α, α1, β, β1, получим
![]() и
и
![]()
Но, согласно формуле призмы δ=(n−1)θ, где n - абсолютный показатель преломления линзы. Поэтому
![]() .
.
В эту формулу тонкой линзы не входит высота h1. Это означает, что расстояние b не зависит от местоположения точки M, т.е. все лучи, исходящие из точки А, соберутся после преломления различными частями линзы в одной точке А1.
