§1.3. Формула призмы

Призмой называется прозрачное тело, с двух сторон ограниченное плоскостями, которые составляют какой-то угол между собой (преломляющий угол призмы – θ, см. рисунок).

После двукратного преломления (на левой и на правой гранях призмы) луч света отклоняется от первоначального направления на угол δ, называемый углом отклонения.

Угол отклонения δ зависит от преломляющего угла θ и показателя преломления n призмы. Эта зависимость легко устанавливается для призмы с малым преломляющим углом (тонкая призма) в случаях малого угла падения α.

δ ≈ (n-1)·θ

(Вывести самостоятельно, учитывая, что при малых значениях θ и α, также малы углы γ, α₁ и γ₁, поэтому из закона преломления sinα=n^.sinγ и n ^. sinα₁=sinγ₁ можно перейти к выражениям α=nγ и nα₁= γ₁, а θ=γ+α₁, δ=(α-γ)+(γ₁- α₁) ).

Минимальный угол отклонения получается в случае симметричного хода луча (т.е. когда α=γ₁ и луч внутри призмы параллелен основанию призмы). Обратите внимание, что при прохождении через призму луч всегда отклоняется в сторону основании.

§1.4. Линзы

Линзы – это прозрачные тела, ограниченные с двух сторон криволинейными (обычно сферическими) поверхностями, преломляющими световые лучи и способные формировать оптические изображения предметов. В частном случае одна из поверхностей может быть плоской

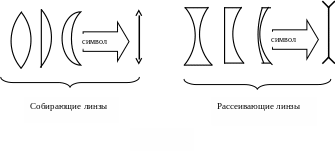
По внешней форме линзы делятся на двояковыпуклые, плосковыпуклые, вогнуто-выпуклые, двояковогнутые, плосковогнутые и выпукло-вогнутые (на рисунке они изображены слева направо). По оптическим свойствам линзы делятся на собирающие (положительные) и рассеивающие (отрицательные). Независимо от внешней формы собирающие линзы посредине толще, чем у краев, в то время, как рассеивающие линзы посредине тоньше, чем у краев.

М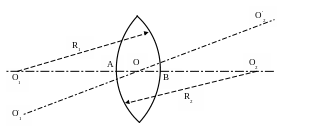 ы будем рассматривать тонкие линзы, толщина которых (расстояние АВ между ограничивающими поверхностями) значительно меньше по сравнению с расстоянием до предмета и с радиусами R₁ и R₂ поверхностей, ограничивающих линзу. В тонких линзах точки А и В расположены столь близко друг от друга, что можно принять их совпадающими с точкой О, называющимися оптическим центром линзы. Лучи света, проходящие через оптический центр линзы, практически не преломляются.

Прямую О₁О₂, проходящую через центры (О₁ и О₂) сферических поверхностей и оптический центр линзы, называют главной оптической осью. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью (на рисунке О^'₁О'₂).

Линзу грубо можно представить как совокупность множества призм. Тогда становится очевидным: собирающие линзы отклоняют лучи к оптической оси, а рассеивающие линзы – от оптической оси.

Параксиальные лучи (т.е. приосевые или околоосевые лучи, которые образуют с оптической осью малые углы), распространяющиеся параллельно главной оптической оси, после преломления сквозь линзу пересекаются в точке, лежащей на этой оси и называемой главным фокусом линзы. У всякой линзы имеются два фокуса по обе стороны от нее (точки F). Расстояние OF=f от оптического центра линзы до ее фокусов называется фокусным расстоянием линзы.

В еличина, обратная фокусному расстоянию, называется оптической силой линзы (D=1/f). Она измеряется в диоптриях (дптр или дп). 1 дптр – оптическая сила линзы с фокусным расстоянием 1м (1 дптр = 1 м^-1).

В отличие от собирающей линзы (левый рисунок а)), рассеивающая линза имеет мнимые фокусы (правый рисунок б)). В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающуюся линзу параллельно главной оптической оси.

Оптическая сила рассеивающей линзы, как ее фокусное расстояние, отрицательная величина.

П лоскость, проведенная через главный фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью. Лучи, падающие на линзу параллельно какой-либо побочной оптической оси, после преломления в линзе, пересекаются в точке, лежащей на фокальной плоскости (побочный или вторичный фокус, на рисунке точка F`). Т.е. фокальная плоскость является геометрическом местом всех вторичных фокусов. У линзы имеются две фокальные плоскости, расположенные на ровных расстояниях по обе стороны от нее.

Построение изображения (А₁В₁) предмета (АВ) в линзах осуществляется с помощью следующих лучей, ход которых нам известен:

1. лучи проходящие через оптический центр линзы не меняют своего направления (на рисунке, I луч);

2. лучи идущие параллельно главной оптической оси, после преломления в линзе (или его продолжение), проходят через второй главный фокус линзы (на рисунке, II луч);

3. лучи (или его продолжения), проходящие через первый главный фокус линзы, после преломления в ней, выходят из линзы параллельно ее главной оптической оси (на рисунке, III луч).

П ересечение любых двух таких лучей (или их продолжений) дает изображение точки предмета, откуда избранные лучи берут начало.

Формула тонкой линзы имеет вид:

,

где a и b – соответственно расстояния от предмета и от его изображения до оптического центра линзы. Эту формулу самостоятельно можно получить, используя подобие треугольников: ΔВАО~ΔВ₁ А₁ О и ΔОСF~ΔB₁ A₁ F .

Более сложный вид формулы тонкой линзы связывает фокусное расстояние f линзы с ее коэффициентом преломления n и радиусами R₁ и R₂ кривизны линзы (знак для радиусов кривизны линз берется положительный - для выпуклых поверхностей и отрицательный – для вогнутых) (см. приложения 2,3,4):

.

Так как фокусное расстояние рассеивающей линзы, как и ее оптическая сила, является отрицательной величиной, то это означает, что в формуле тонкой линзы a и b, в определенных случаях, должны иметь отрицательные значения. Правила, при помощи которых можно определить знаки a и b, в разных учебниках освещаются по-разному. Наиболее запоминающими, с моей точки зрения, являются правила, основанные на опыте повседневной жизни. Для этого надо только запомнить:

• У собирающих линз f и D положительны, а у рассеивающих линз – отрицательны;

• a всегда положительны;

• b положительны, если изображения действительные, и отрицательны у мнимых изображений.

Отношение линейных размеров изображения и предмета называется линейным увеличением линзы (А₁В₁/АВ). Отрицательным значением линейного увеличения соответствует действительное изображение (оно перевернутое), положительным – мнимое изображение (оно прямое).

Нижеследующая таблица показывает характер изображения собирающей линзы в зависимости от расстояния предмета до линзы.